二叉树

经典题目

当前 root 节点 【该做什么】【什么时候做】

226.翻转二叉树

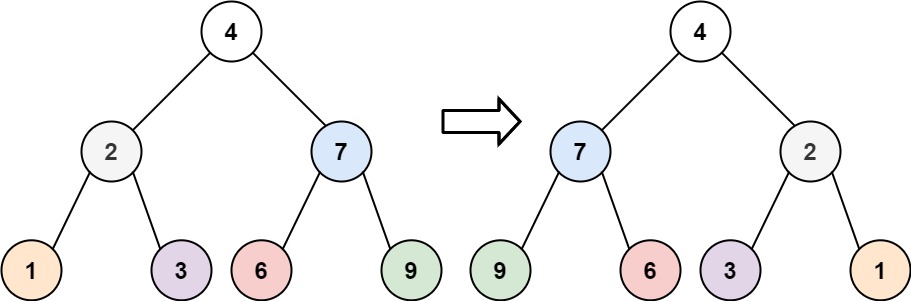
xxxxxxxxxx
// 该做什么：对于当前 root 节点，交换左右子树
// 什么时候做：先序遍历 || 后序遍历

public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;
    
    // 先序遍历的处理阶段（交换左右子树）
    TreeNode leftNode = root.left;
    TreeNode rightNode = root.right;
    root.left = rightNode;
    root.right = leftNode;

    // 递归处理左右子树
    invertTree(leftNode);
    invertTree(rightNode);

    return root;
}

public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;

    // 递归处理左右子树
    TreeNode leftNode = invertTree(root.left);
    TreeNode rightNode = invertTree(root.right);

    // 后序遍历的处理阶段
    root.left = rightNode;
    root.right = leftNode;

    return root;
}

100.相同的树

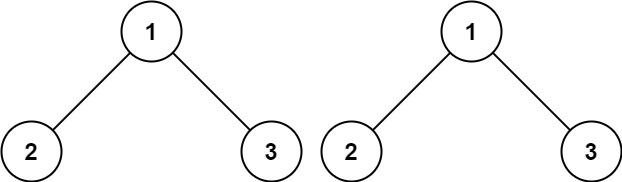
xxxxxxxxxx
// 该做什么：对于当前 root 节点，判断是否相同（值相同）
// 什么时候做：先序遍历（先判断根是否相同，如果相同递归判断左右子树是否相同）

public boolean isSameTree(TreeNode p, TreeNode q) {
    // 先序遍历的处理阶段
    if (p == null || q == null) return p == q;
    if (p.value != q.value) return false;
    
    // 递归处理左右子树
    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}

101.对称二叉树

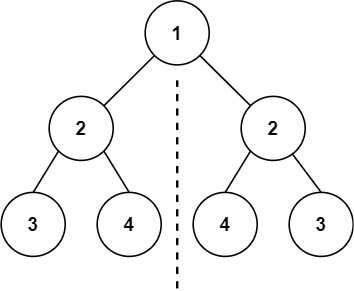
xxxxxxxxxx
// 该做什么：对于当前 root 节点，判断左右子树是否对称（需要增加参数）
// 什么时候做：先序遍历

/**
 * 判断是否为对称二叉树
 * @param root 根节点
 * @return boolean
 */
public boolean isSymmetric(TreeNode root) {
    if (root == null) return true;
    return isSymmetricHelper(root.left, root.right);
}

/**
 * 判断对称二叉树的帮助函数
 * @param leftTree left tree
 * @param rightTree right tree
 * @return boolean
 */
public boolean isSymmetricHelper(TreeNode leftTree, TreeNode rightTree) {
    // 先序遍历处理阶段
    if (leftTree == null || rightTree == null) return leftTree == rightTree;
    if (leftTree.value != rightTree.value) return false;
    
    // 递归处理左右子树
    return isSymmetricHelper(leftTree.left, rightTree.right) && isSymmetricHelper(leftTree.right, rightTree.left);
}

116.填充每个节点的下一个右侧节点指针

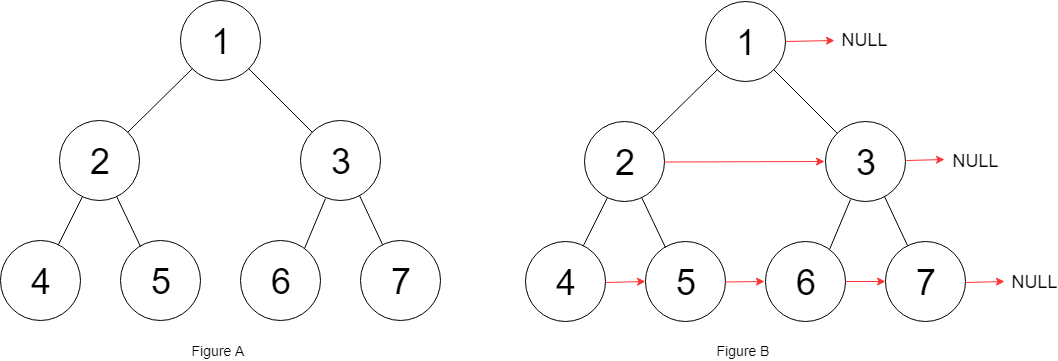
xxxxxxxxxx
// 该做什么：对于当前节点，把左节点的 next 指向 右节点（一个参数做不到 / 切记每次都只考虑当前节点，不要考虑孩子节点）
// 什么时候做：先序遍历

/**
 * 填充每个节点的下一个右侧节点指针
 * @param root 根节点
 * @return root
 */
public Node connect(Node root) {
    if (root == null) {
        return null;
    }
    connectHelper(root.left, root.right);
    return root;
}

/**
 * 填充每个节点的下一个右侧节点指针 帮助函数
 * @param leftTree left tree
 * @param rightTree right tree
 */
public void connectHelper(Node leftTree, Node rightTree) {
    // 先序遍历处理阶段
    if (leftTree == null || rightTree == null) {
        return;
    }
    leftTree.next = rightTree;
    // 递归
    connectHelper(leftTree.left, leftTree.right);
    connectHelper(leftTree.right, rightTree.left);
    connectHelper(rightTree.left, rightTree.right);
}

104.二叉树最大深度

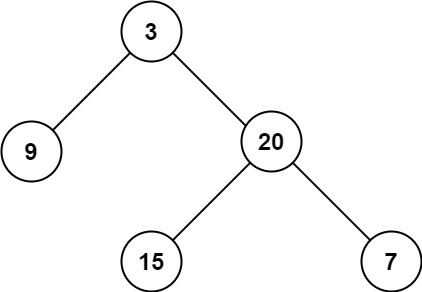
xxxxxxxxxx
// 该做什么：对于当前节点，如果为 null，则返回 0，表示深度为 0，如果非空则和深度更大的子树 +1
// 什么时候做：先序遍历

public int maxDepth(TreeNode root) {
    // 先序遍历处理阶段
    if (root == null) return 0;
    // 递归，选择深度更大的子树
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

111.二叉树最小深度

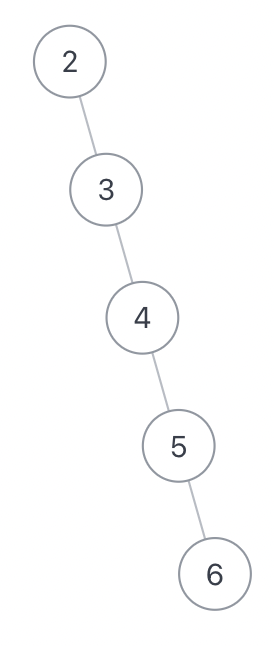
xxxxxxxxxx
public int minDepth(TreeNode root) {
    if (root == null) return 0;
    
    // 不同之处：如果不加此判断，左右孩子有一个为 null 时，会选择为空的子孩子
    if (root.left == null) return minDepth(root.right) + 1;
    if (root.right == null) return minDepth(root.left) + 1;

    return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
}

671.二叉树中第二小的节点

xxxxxxxxxx
// 递归：分解子问题
// 当前节点：root
// 该做什么：如下
// 什么时候做：后序遍历
// 返回值：第二小节点值
// 前提：root 是最小节点
public int findSecondMinimumValue(TreeNode root) {
    // 如果无孩子节点，则不存在第二小节点
    if (root.left == null && root.right == null) return -1;
    // 记录左右孩子值
    int left = root.left.val;
    int right = root.right.val;
    // 如果 root 值等于左孩子值，则去左子树找
    if (root.val == left) {
        left = findSecondMinimumValue(root.left);
    }
    // 如果 root 值等于右孩子值，则去右子树找
    if (root.val == right) {
        right = findSecondMinimumValue(root.right);
    }
    // --------------- 处理过程 ---------------
    // 如果左孩子没找到，则右孩子是第二小节点
    if (left == -1) return right;
    // 如果右孩子没找到，则左孩子是第二小节点
    if (right == -1) return left;
    // 如果左右孩子都找到了第二小值，则取两者最小值
    return Math.min(left, right);
}

993.二叉树的堂兄弟节点

// 善于运用全局变量
TreeNode parentX = new TreeNode(-1);
TreeNode parentY = new TreeNode(-1);
int depthX = 0;
int depthY = 0;
int x;
int y;
public boolean isCousins(TreeNode root, int x, int y) {
    this.x = x;
    this.y = y;
    traversal(root, null, 0);
    if (depthX == depthY && parentX != parentY) return true;
    return false;

}
private void traversal(TreeNode root, TreeNode parent, int depth) {
    if (root == null) return ;
    if (root.val == x) {
        parentX = parent;
        depthX = depth;
    }
    if (root.val == y) {
        parentY = parent;
        depthY = depth;
    }
    traversal(root.left, root, depth + 1);
    traversal(root.right, root, depth + 1);
}