二叉树「遍历」And「分解」

226. 翻转二叉树

114. 二叉树展开为链表

116. 填充每个节点的下一个右侧节点指针

在 二叉树--纲领篇 中，介绍了解决二叉树问题无非就是「遍历」➕「分解」两种方法

对于遇到的题目，我们的思路就是：是否可以通过遍历一遍二叉树得到答案？如果不能的话，是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案? 如果需要设计到子树信息, 建议使用后续遍历

下面本篇文章，将按照这个思路，手把手的带你解决三个实战题目

翻转二叉树

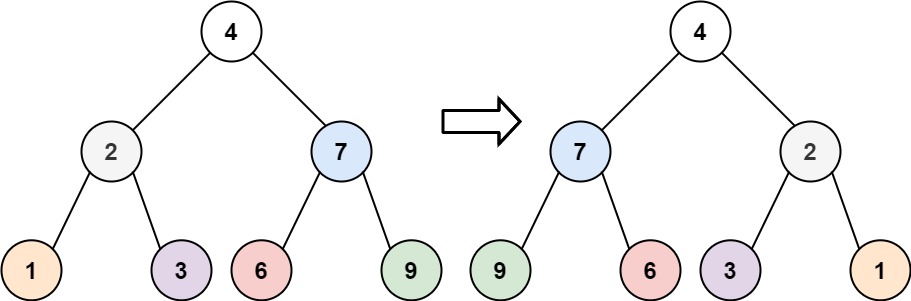
对于这个题目的要求就是「翻转整棵树」

首先我们思考一下，是否可以通过遍历一遍二叉树得到答案呢？？

• 显然是可以的！很简单，当我们前序遍历首次进入节点时，执行操作「交换 root.left 和 root.right」

xxxxxxxxxx
public void traversal(TreeNode root) {
    if (root == null) return ;
    // 前序阶段：交换左右子树
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;
    
    traversal(root.left);
    traversal(root.right);
}

那我们现在继续思考是否可以使用分解的思路来解决问题呢？？

• 显然也是可以的！我们在「后序遍历」阶段执行我们的逻辑操作
• 后序处理阶段，表明此时左右子树都是完成了翻转

xxxxxxxxxx
// 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点
public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;
    TreeNode left = invertTree(root.left);
    TreeNode right = invertTree(root.right);
    // 后序阶段：交换左右子树
    root.left = right;
    root.right = left;
    // 和定义逻辑自恰：以 root 为根的这棵二叉树已经被翻转，返回 root
    return root;
}

在使用分解的思路时，我们需要明确「函数返回值」代表的含义，即：给递归函数一个合适的定义，然后用函数的定义来解释你的代码

二叉树展开为链表

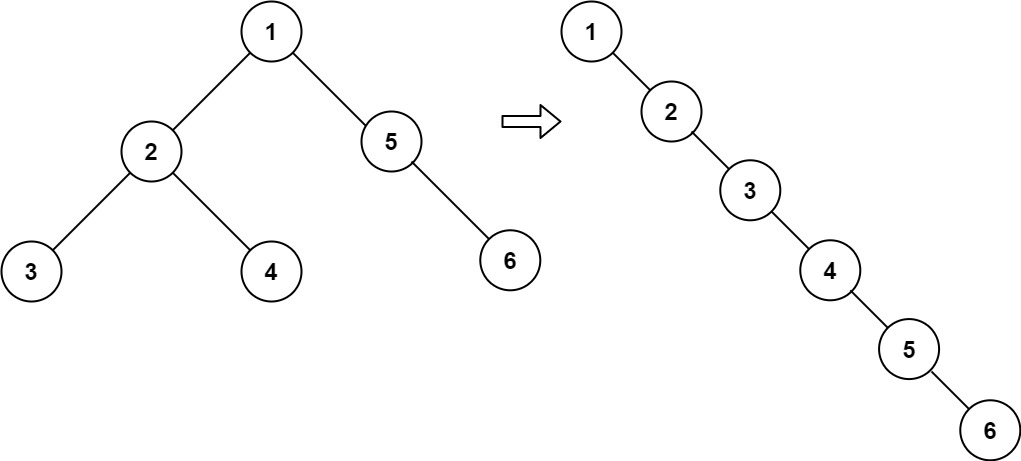
对于这个题目的要求就是「拉平左子树，接到右子树上」

首先我们思考一下，是否可以通过遍历一遍二叉树得到答案呢？？

• 乍一看感觉是可以的：对整棵树进行前序遍历，一边遍历一边构造出一条「链表」就行了

​x
// 虚拟头节点，dummy.right 就是结果
TreeNode dummy = new TreeNode(-1);
// 用来构建链表的指针
TreeNode p = dummy;

public void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    p.right = new TreeNode(root.val);
    p = p.right;

    traverse(root.left);
    traverse(root.right);
}

但是注意flatten函数的签名，返回类型为void，也就是说题目希望我们在原地把二叉树拉平成链表

这样一来，没办法通过简单的二叉树遍历来解决这道题了

那我们现在继续思考是否可以使用分解的思路来解决问题呢？？

• 显然是可以的！很简单，当我们后序遍历离开节点时，执行操作「连接左子树到右子树上」
• 后序遍历离开节点时，表示此时左右子树均为拉直状态，如上图中间状态

xxxxxxxxxx
// 定义：将以 root 为根的这棵二叉树拉直，返回拉直后的二叉树根节点
private TreeNode traversal(TreeNode root) {
    if (root == null) return root;
    TreeNode left = traversal(root.left);
    TreeNode right = traversal(root.right);
    // 后序阶段
    root.left = null;
    root.right = left;
    TreeNode p = root;
    while (p.right != null) {
        p = p.right;
    }
    p.right = right;
    // 和定义逻辑自恰：以 root 为根的这棵二叉树已经被拉直，返回 root
    return root;
}

填充每个节点的下一个右侧节点指针

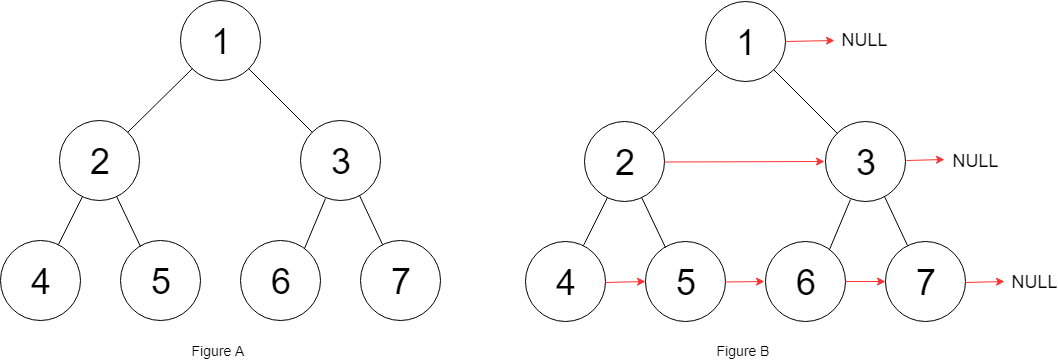
对于这个题目的要求就是「node.next = leftNode」

首先我们思考一下，是否可以通过遍历一遍二叉树得到答案呢？？

• 貌似是不可以的！！因为遍历只能实现root.left.next = root.right，而对于节点5和6是无法连接起来的

但是如果我们在二叉树的遍历基础上抽象成「三叉树遍历」呢？？？直接看图！！！

OK！直接看代码！！

public void traversal(TreeNode node1, TreeNode node2) {
    if (node1 == null || node2 == null) return ;
    // 前序：执行连接操作
    node1.next = node2;
    
    traversal(node1.left, node1.right);
    traversal(node1.right, node2.left);
    traversal(node2.left, node2.right);
}