岛屿数量「变题」

开头先来一个小插曲，关于「岛屿」类题目的总结可见 秒杀所有岛屿题目(DFS)

DFS


x
// 时间复杂度 : O(mn)
// 空间复杂度 : O(mn) -> 最坏全部是 1，栈空间需要 O(mn)
private int m, n;
private char[][] grid;
private int[][] dirs = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
public int numIslands(char[][] grid) {
    this.grid = grid;
    m = grid.length; n = grid[0].length;
    int ans = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == '1') {
                f(i, j);
                ans++;
            }
        }
    }
    return ans;
}
private void f(int i, int j) {
    if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') return ;
    grid[i][j] = '0';
    for (int[] dir : dirs) {
        f(i + dir[0], j + dir[1]);
    }
}

BFS


xxxxxxxxxx
// 时间复杂度 : O(mn)
// 空间复杂度 : O(min(m, n)) -> 见下图
private int[][] dirs = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
public int numIslands(char[][] grid) {
    int ans = 0;
    int m = grid.length, n = grid[0].length;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == '1') {
                grid[i][j] = '0';
                Queue<int[]> q = new LinkedList<>();
                q.offer(new int[]{i, j});
                while (!q.isEmpty()) {
                    int[] cur = q.poll();
                    for (int[] dir : dirs) {
                        int nx = cur[0] + dir[0], ny = cur[1] + dir[1];
                        if (nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] == '0') continue;
                        q.offer(new int[]{nx, ny});
                        grid[nx][ny] = '0';
                    }
                }
                ans++;
            }
        }
    }
    return ans;
}

$O(\min(m, n))$

假设最坏的情况：所有地方都是岛屿，从(0, 0)开始搜索，结合 BFS 的特点，如下图所示

每一种颜色表示队列需要容纳的元素个数，最大为 4，也就是 min(m,n)

注意：这是从(0, 0)开始搜索，如果换一个点开始搜索，结果就会不同，如下图所示

绿色和橙色的数量最多 (7 个)，表示队列最多需要容纳 7 个元素

并查集


// 时间复杂度 : O(mn)
// 空间复杂度 : O(mn)
private int N;
private int[] parent;
public int numIslands(char[][] grid) {
    int m = grid.length, n = grid[0].length;
    N = m * n;
    parent = new int[N];
    for (int i = 0; i < N; i++) parent[i] = i;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i - 1 >= 0 && grid[i][j] == grid[i - 1][j]) union(i * n + j, (i - 1) * n + j);
            if (i + 1 < m && grid[i][j] == grid[i + 1][j]) union(i * n + j, (i + 1) * n + j);
            if (j - 1 >= 0 && grid[i][j] == grid[i][j - 1]) union(i * n + j, i * n + j - 1);
            if (j + 1 < n && grid[i][j] == grid[i][j + 1]) union(i * n + j, i * n + j + 1);
        }
    }
    Set<Integer> set = new HashSet<>();
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == '1') set.add(find(i * n + j));
        }
    }
    return set.size();
}
private void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ) return ;
    parent[rootP] = rootQ;
}
// 执行次数多了后为常数时间
private int find(int x) {
    if (x != parent[x]) parent[x] = find(parent[x]);
    return parent[x];
}

解释：find()方法使用了路径压缩，每执行一次就会将树拉平一部分，详情可见 并查集（Union-Find）

变题一：岛屿的最大面积

题目详情可见岛屿的最大面积

变题二：加一个陆地后最大岛屿面积

题目详情可见最大人工岛

变题三：岛屿的周长

题目详情可见岛屿的周长

变题四：统计封闭岛屿的数目 (四周没有封闭)

题目详情可见统计封闭岛屿的数目

变题五：修改封闭区域

题目详情可见被围绕的区域

变题六：统计子岛屿

题目详情可见统计子岛屿

变题七：太平洋大西洋水流问题

题目详情可见太平洋大西洋水流问题

变题八：BFS 典型应用

题目详情可见腐烂的橘子

BFS 的典型应用！！！

变题九：不同形状岛屿的数量

题目详情可见不同岛屿的数量

由于这是一道会员题，给出题目描述的截图，如下图所示

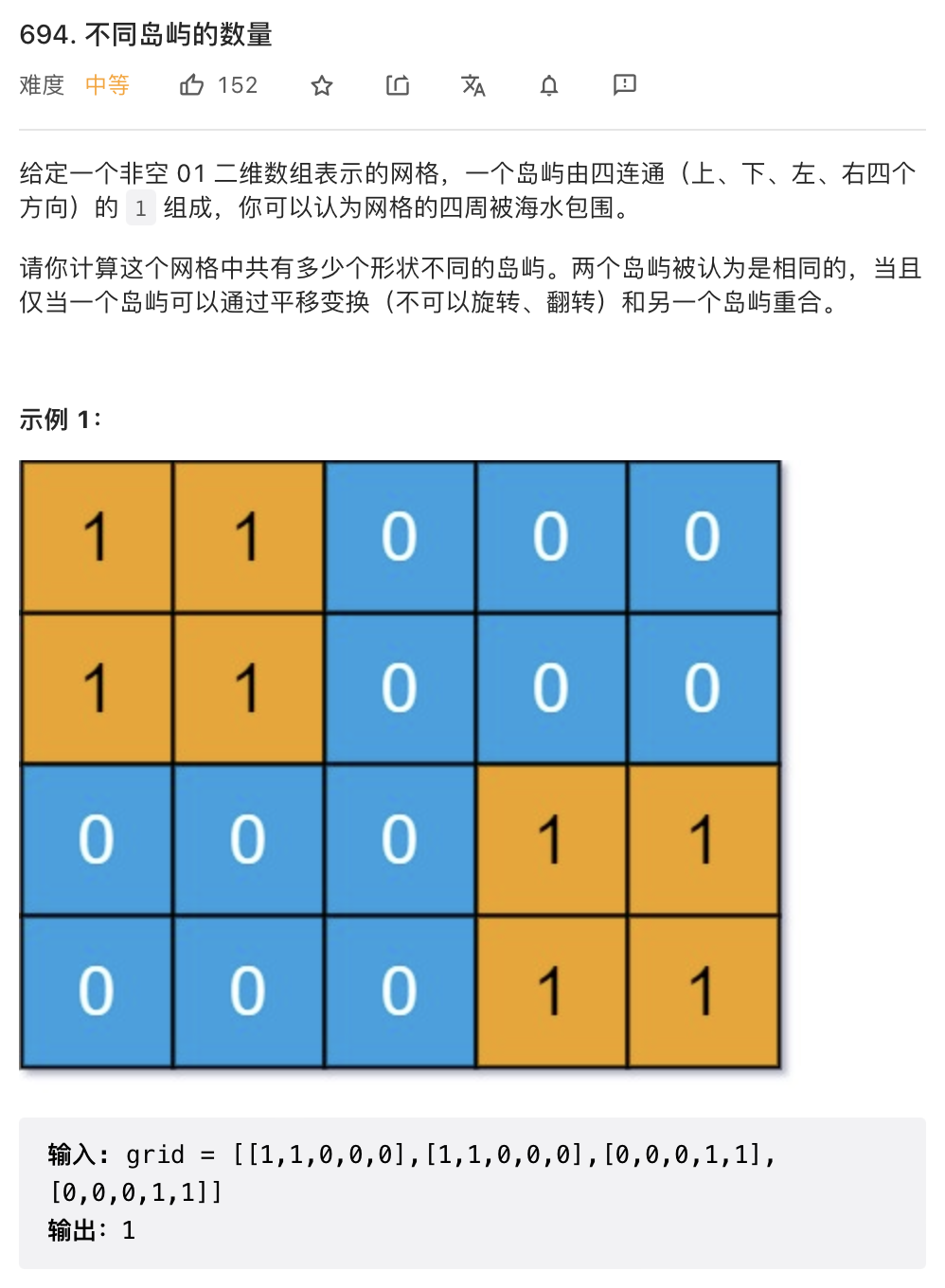
这个题目和 寻找重复的子树 如出一辙，通过记录路径，然后借助Set去重


xxxxxxxxxx
private int m, n;
private int[][] grid;
private Set<String> set = new HashSet<>();
public int numDistinctIslands(int[][] grid) {
    m = grid.length; n = grid[0].length;
    this.grid = grid;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 1) {
                set.add(dfs(i, j, ""));
            }
        }
    }
    return set.size();
}
private String dfs(int i, int j, String s) {
    if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0) return "NUll";
    grid[i][j] = 0;
    return s + dfs(i + 1, j, "D") + dfs(i - 1, j, "U") + dfs(i, j + 1, "R") + dfs(i, j - 1, "L");
}