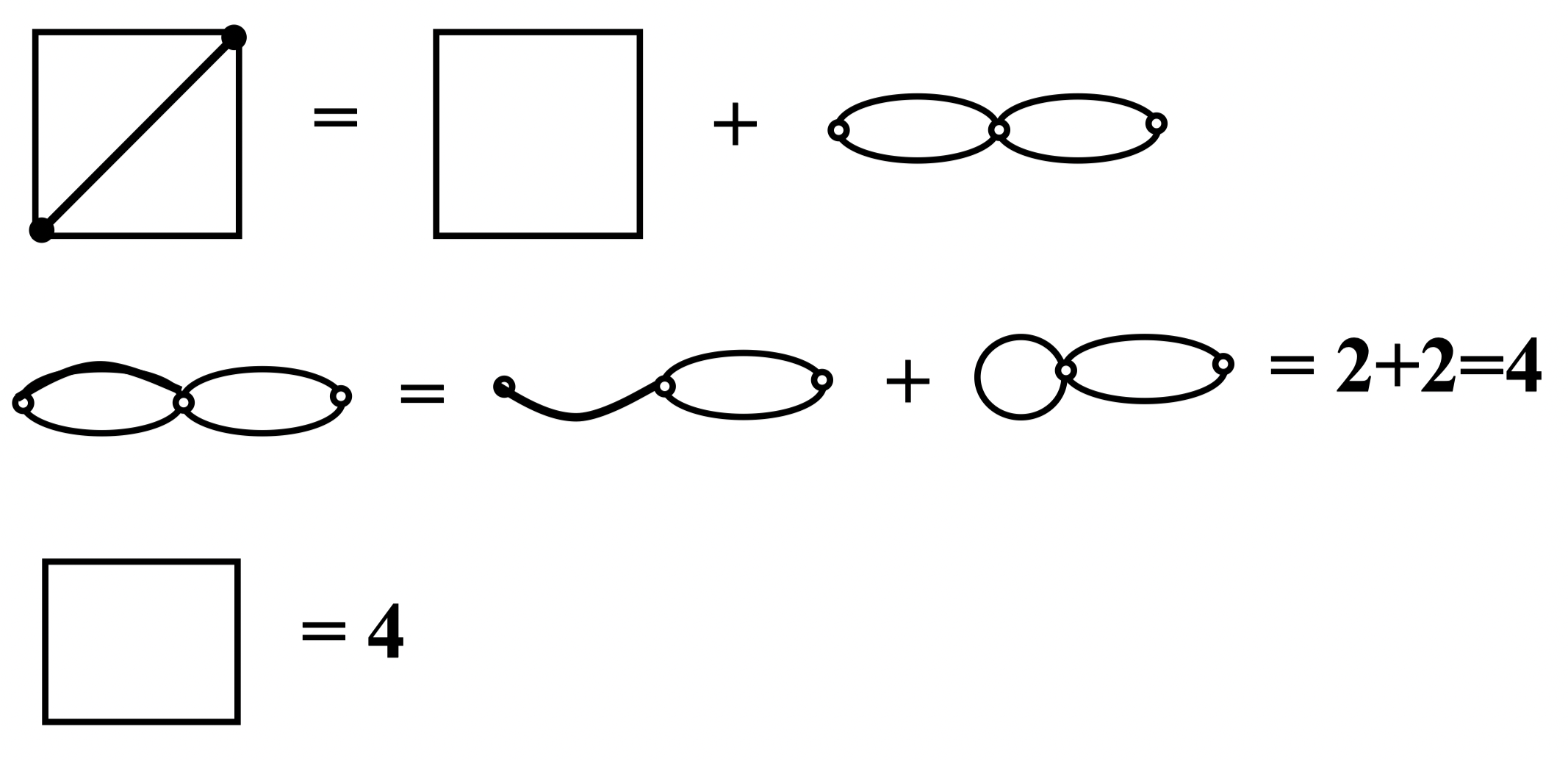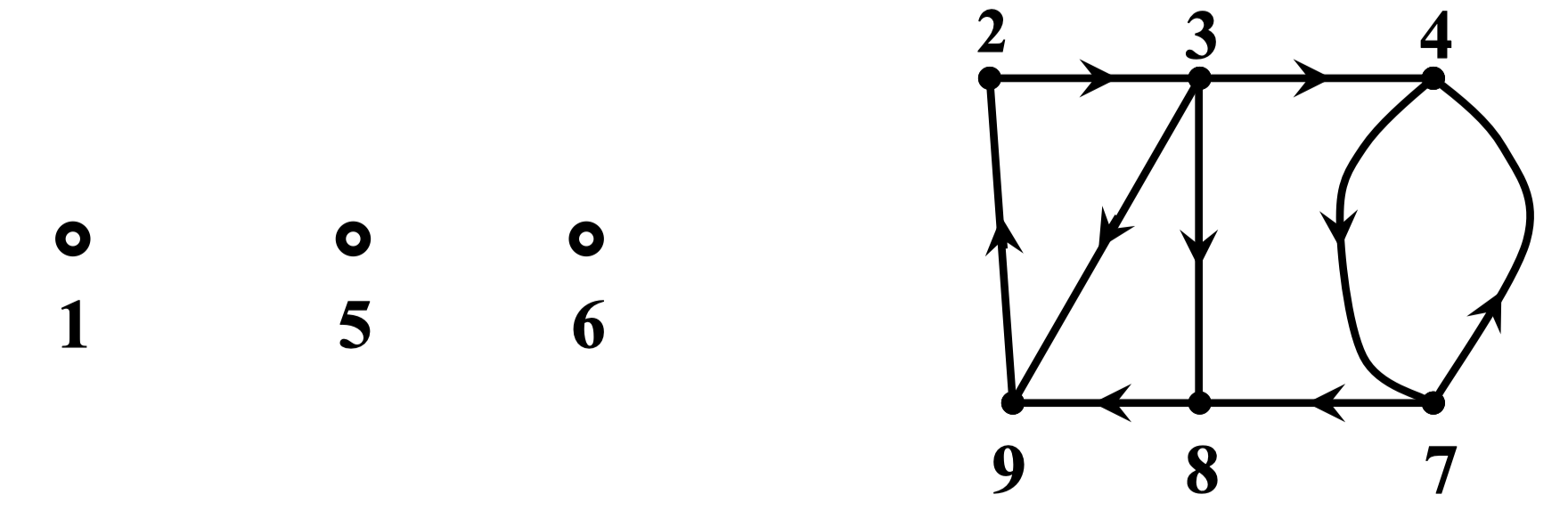图论
第一章 图的基本概念
图的定义
定义 1:一个图 定义为一个有序对 ,记为 ,其中:
- 是一个非空集合,称为顶点集或点集,记为 ,其元素称为顶点或点
- 是由 中的点组成的无序点对构成的集合,称为边集,记为 ,其元素称为边,且同一点对在 中可出现多次
 注意: -> 顶点数(或阶数) -> 边数
注意: -> 顶点数(或阶数) -> 边数
相关概念
- 相关联:若边 ,此时称 和 是 的端点;并称 和 相邻,(或 ) 与 相关联
- 相邻:若两条边有一个共同的端点,则称这两条边相邻
- 孤立点:不与任何边相关联的点
- 自环(环):两端点重合的边
- 重边:连接两个相同顶点的边的条数,叫做边的重数。重数大于 1 的边称为重边
- 有限图:点集与边集均为有限集合的图标称为有限图
- 平凡图:只有一个顶点而无边的图称为平凡图
- 空图:边集为空的图称为空图
- 简单图:即没有自环也没有重边的图称为简单图
- 复合图:除去简单图,其他图都称为复合图
图的同构
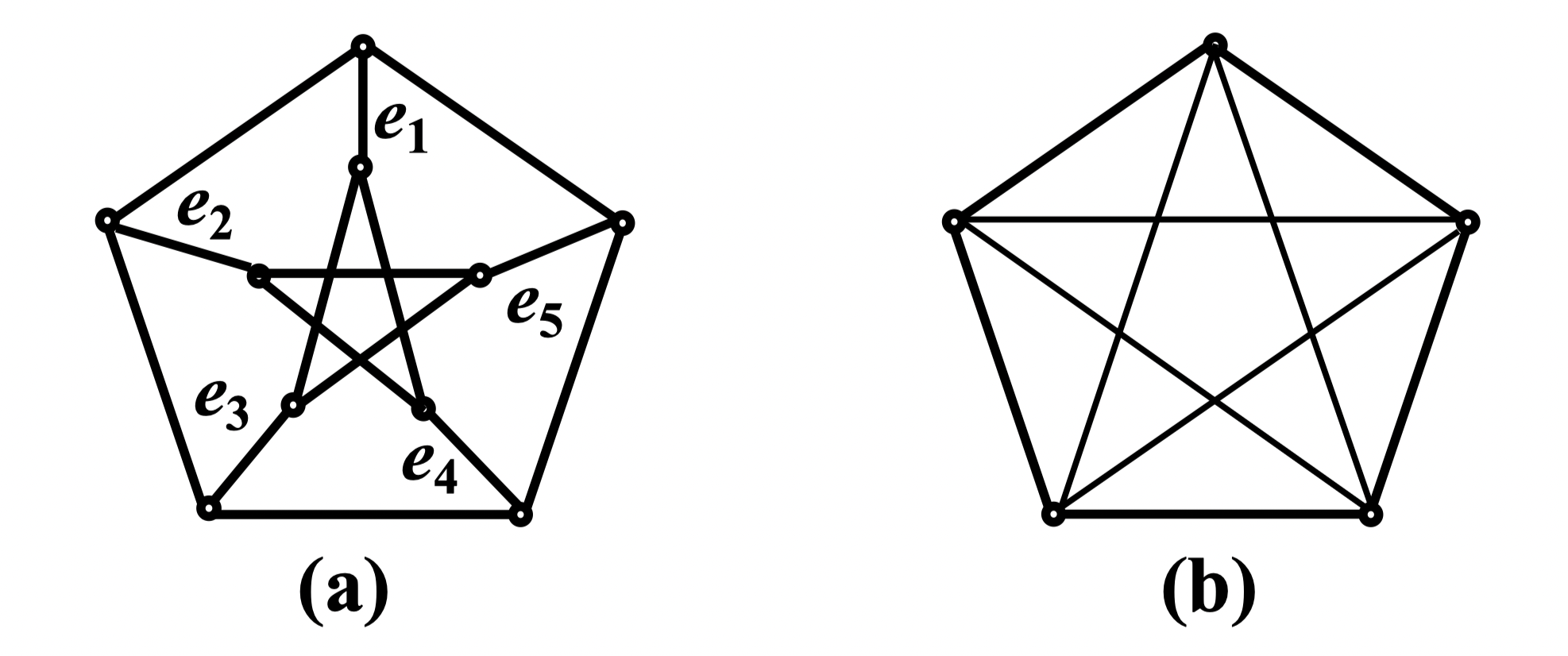
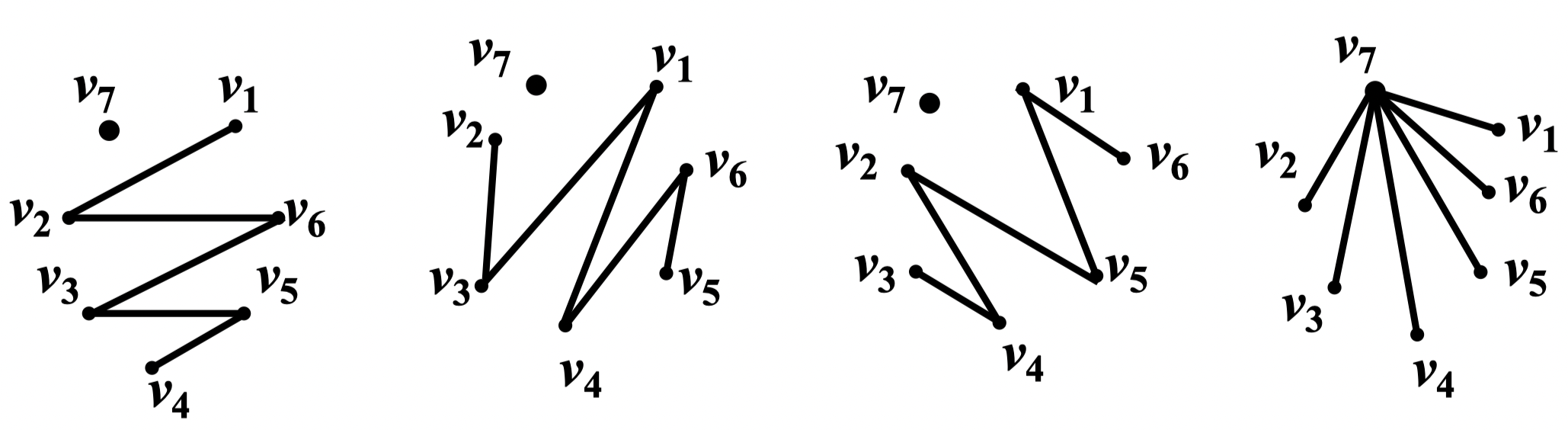
定义 2:设有两个图 和 ,若在其顶点集合之间存在双射,即存在一一对应的关系,使得边之间有如下的关系:设 , ,,, 当且仅当 ,且 的重数与 相等,则称两图同构,记为
 注意
注意
- 两个同构的图均有相同的结构,没有本质的差异,差异只是顶点和边的名称不同
- 图同构的几个必要条件:1. 顶点数相同;2. 边数相同;3. 若将各点所关联的边数记录下来,则所得到的数组相同
- 在图的图形表示中可以不给图的点和边标号,称这样的图为非标定(号)图,否则称为标定(号)图。非标定图实际上是代表一类相互同构的图。不误解时我们也不严格区分标定图与非标定图
- 判定图的同构是很困难的。对于规模不大的两个图,判定其是否同构,可以采用观察➕推证的方法
完全图 & 偶图 & 补图
定义 3:任意两点均相邻的简单图称为完全图,在同构意义下, 阶完全图只有一个,记为 ,其中
定义 4:若一个图的点集可以分解为两个(非空)子集 和 ,使得每条边的一个端点在 中,另一个端点在 中,则这样的图称为具有二分类 的偶图(或二部图)
- 完全偶图 是指具有二分类 的简单偶图,其中 的每个顶点与 的每个顶点相连,若 ,则这样的偶图记为
定义 5:设 ,则图 称为 的补图,记为 ,其中集合 ,
 解释: 包含所有 的二元子集;
解释: 包含所有 的二元子集;
定理 1:若 阶图 是自补的(即 ),则
证明:因为 是自补的,则 和其补图有同样多的边数,且边数满足:,从而:
又因 的边数 是整数,故 为整数,即只能有 或
度 & 度序列
定义 6:设 为 的顶点, 中以 为端点的边数的条数(环计算两次)称为点 的度数,简称为点 的度,记为 ,简记为
相关术语和记号
- :图 的顶点的最小度
- :图 的顶点的最大度
- 奇点:度数为奇数的顶点
- 偶点:度数为偶数的顶点
- 正则图:每个点的度均为 的简单图
例如:完全图 和完全偶图 均为正则图
定理 2 (握手定理):对任意的有 条边的图 ,有
推论 1:任意图中,奇点的个数为偶数
证明:设 , 分别是由 的奇点和偶点构成的集合,则由欧手定理知:
显然第二个求和式为偶数,而第一个求和式中的每一项都为奇数,所以第一个求和式必然有偶数项,即度数为奇数的顶点个数必为偶数
推论 2:正则图的阶数和度数不 同时 为奇数(有歧义,注意断句!!!即阶数和度数不能均为奇数)
证明:设 是 正则图,若 为奇数,则由推论 1 知正则图 的点数必为偶数
例:设 与 是简单图 的最大度与最小度,求证:
证明:由握手定理知:;所以:
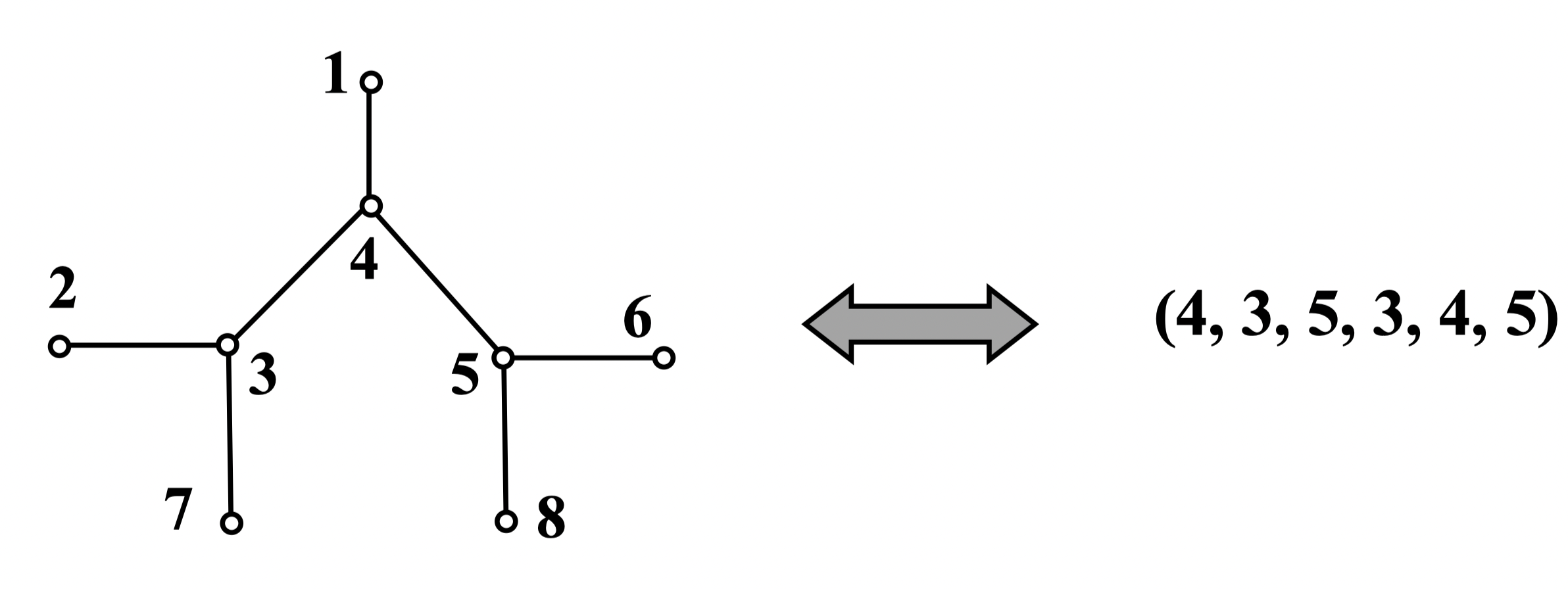
定义 7:一个图 的各个点的度 构成的非负整数组 称为 的度序列
定理 3:非负整数组 是图的度序列的充分必要条件是: 为偶数
证明:必要性由握手定理立即可得,即:非负整数组 是图的度序列 -> 为偶数
如果 为偶数,则数组中奇数的个数必为偶数
按照如下方式作图 :若 为偶数,则在与之对应的点作 个环;对于剩下的偶数个奇数 ,两两配对后分别在每配对点间先连一条边,然后在每个顶点作 个环
该图的度序列就是已知数组,即: 为偶数 -> 非负整数组 是图的度序列
定义 8:对于一个非负整数组 ,若存在一个简单图,以它为度序列,则称这个数组是可图的。可图的序列简称为可图序列或图序列
主要研究 3 个问题
- 判定问题:什么样的整数数组是可图序列?
- 计数问题:一个可图序列对应多少不同构的图?
- 构造问题:如何画出可图序列对应的所有不同构的图?
定理 4 (Havel-Hakimi 定理):设有非负整数组 满足 ,,则 是可图序列的充分必要条件是: 是可图的
解释 的构成:序列 中有 个非负整数,序列 中 后的前 个度数(即 )减 1 后构成 中的前 个数
证明:充分性显然(原因:可以把 非递增排列)
必要性:设 是 对应的简单图,
- 情形一:点 与点 邻接,则删去顶点 及其关联的边所得到的图的度序列正好为
- 情形二:(待补充。。。)
例:试判断非负整数组 是否可图?
解:根据定理可得下列非负整数组
- ->
显然 是可图序列,因此 是可图的
度的频序列
定理 5:一个简单图 的 个点的度不能互不相同
证明:因为图 为简单图,所以
情形一:若 没有孤立点,则 ,。因为顶点个数为 ,所以必有两个顶点度数相同 -> 包含 个整数,而有 个顶点,故至少存在一个顶点和其他的顶点度数相同
情形二:若 仅存在一个孤立点,设 表示 去掉孤立点后的部分,则 。同理,在 中必有两顶点度数相同
情形三:若 有两个以上的孤立点,则定理显然成立 -> 存在两个以上度数为 0 的顶点
定义 9:设 阶图 的各点的度数取 个不同的非负整数 。又设度为 的点有 个(),则称 为 的频序列 -> 频序列表示每个度数出现的频率的数组序列
定理 6:一个 阶图 和它的补图有相同的频序列
证明:由补图的定义知,点 在图 及其补图中的度数之和为 ,即:
因此,若 中有 个度为 的点,则这 个点在 的补图中的度变为
故 与其补图有相同的频序列
子图
定义 10:设 和 为两个图,若 , 且 中边的重数不超过 中对应边的重数,则称 是 的子图,记为 ,有时又称 是 的母图
 注意
注意
- 简单地说,图 的任意一部分(包括 自身和空图)都称为是图 的一个子图
- 当 ,但 ,则记为 ,且称 为 的真子图
- 的生成子图是指满足 的子图 -> 中的顶点集合和 中的顶点集合相同
定义 11:设 是 的一个非空子集。以 为顶点集,以两端点均在 中的边的全体边集所组成的子图,称为 的由 导出的子图,记为 ;简称为 的导出子图 -> 又称 的点导出子图
 注意
注意
- 表示从 中删除 中顶点以及与这些顶点相关联的边所得到的子图。若 ,则把 简记为
- 其中:
定义 12:假设 是 的非空子集。以 为边集,以 中边的端点全体为顶点集所组成的子图称为 的由 导出的子图,记为 ,简称为 的边导出子图
 注意
注意
- 表示从 中删除 中的边之后的子图。若 ,则把 简记为
- 其中: 可能会比 多一些点
对比: &&
主要区别: 删除顶点后会把顶点相关联的边也删除;而 仅删除对应的边,可能会留下一些孤立的点
图的运算
相关术语和概念
和 不相交:无公共顶点
和 边不重:无公共边
并图 :顶点集为 ,边集为 的图 的一个子图;如果 和 是不相交的,就记其并图为
交图 :类似并图的定义,但二者至少要有一个公共顶点
差图 :在 中去掉 中的边组成的图
对称差 :
定义 13:在不相交的 和 的并图 中,把 的每个顶点和 的每个顶点连接起来所得到的图称为 和 的联图,记为
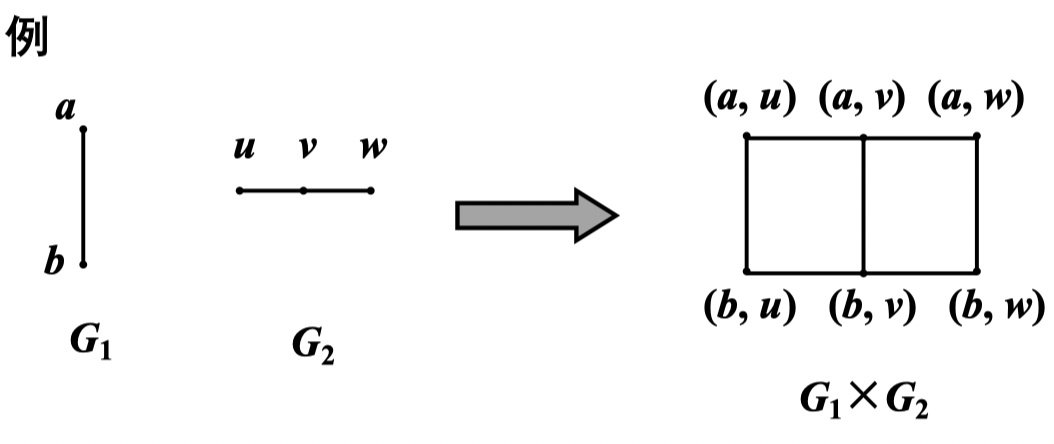
定义 14:设 ,,对点集 中的任意两个点 和 ,当 或 时就把 和 连接起来所得到的图 称为 和 的积图,记为 ,其中 表示 和 邻接
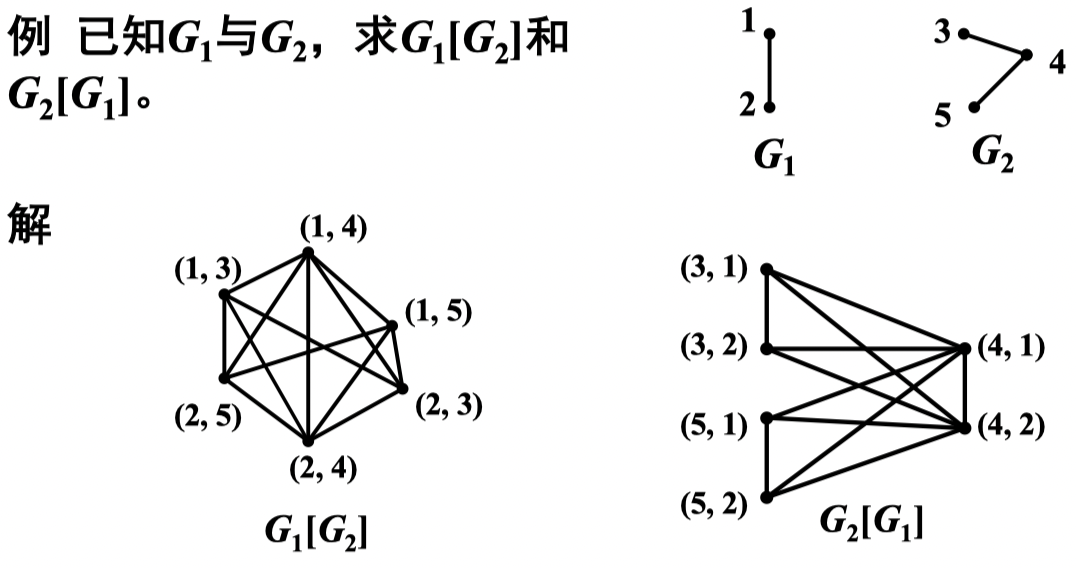
定义 15:设 ,,对点集 中的任意两个点 和 ,当 或 时就把 和 连接起来所得到的图 称为 和 的合成图,记为
汇总:若 的点数和边数为 ,,若 的点数和边数为 ,,经过联、积、合成三种运算,图的点数和边数为:
| 运算 | 点数 | 边数 |
|---|
| | |
| | |
| | |
| | |
定义 16:把 的任意一个顶点和 的任意一个顶点等同起来得到新图称为 与 的联合,记为
途径 & 迹 & 路 & 圈 & 距离 & 直径
定义 17:给定图 , 是 中点边交替组成的序列,其中 ,,若 满足 的端点为 与 ,则称 为一条从顶点 到顶点 的途径(或通道或通路),简称 途径
- 顶点和分别称为的起点和终点,其他点称为内部点,途径中的边数称为它的长度
- 在简单图中,途径可以简单地由其顶点序列来表示
定义 18:边不重复的途径称为迹;点不重复的迹称为路
定义 19:起点和终点相同的途径、迹和路分别称为闭途径(也称为环游)、闭迹(也称为回路)和圈
 注意
注意
若图中两个不同点 与 间存在途径,则 与 间必存在路 途径 路
从途径中删除重复的点和边即变成路
若过点 存在闭迹,则过点 必存在圈 闭迹 圈
从闭迹中删除重复的点即变成圈
若过点 存在闭途径,则过点 不一定存在圈 闭途径 圈
闭途径可能存在一种情况,即在重边时无环,但也为闭途径的情况
闭途径:,但是却不存在圈
闭迹刚好避免了上述的情况,所以可以 闭迹 圈
定义 20:联结 和 的长度最短的路的长度,称为 与 的距离,记为
定义 21:图 的直径定义为
 例:完全图的直径是 1
例:完全图的直径是 1
例:在图 中,取 ,,,则:
- 是长度为 2 的路
- 是长度为 4 的迹
- 是长度为 5 的途径
- 是长度为 3 的圈
- 是长度为 6 的回路
- 直径
图的连通性
定义 22:图 中点 与 称为是连通的,如果 与 间存在途径;否则称 与 不连通
定义 23:如果图 中任意两点是连通的,称 是连通图,否则称图 是非连通图。在图中,每一个极大的连通部分称为 的连通分支。 的连通分支的个数,称为 的分支数,记为
例:连通图,;非连通图,
例:证明:在 阶连通图中,(1) 至少有 条边;(2) 如果边数大于 ,则至少有一个圈
证明:(1) 对 的顶点数作数学归纳
(2) 对于简单图,结论显然成立。故假设 是简单图
任取 的一条边 ,显然 满足「边数 = 点数 - 1」
由于 是连通图,必然存在一点 ,它不在 上,但与 上的某一点相邻,不妨假设该点为
将边 添加到 上,得到一个包含 2 个点的连通子图 。显然 也满足「边数 = 点数 - 1」
如此不断下去,最终会得到一个连通的生成子图 ,其边数正好等于
但由于 的边数大于 ,因此存在两个不同的顶点 与 ,它们在 中不相邻,但在 中相邻
从而,边 以及 中连接 与 的路便构成了一个圈
例:证明:若 ,则 中必然含有圈
证明:只就连通的简单图证明即可!
设 是 中的一条最长子路
由于 ,所以 必然有相异于 的相邻顶点
又因为 是 中最长路,所以这样的点必然是 中之一
设该点为 ,则 为 中的一个圈
例:设 是具有 条边的 阶简单图,证明:若 的直径为 2 且 ,则
证明:设 ,且设 的邻接点为 , 是剩下的一个顶点
由于 且 不能和 相邻,所以 至少和 中的一个顶点邻接,否则有 (非连通图的直径定义为 )
不妨假设 和 相邻
为了保证 到各点距离不超过 2, 这些顶点的每一个必须和前面 中某点相邻,这样图中至少又有 条边
因此,总共至少有 条边
定理 7:若图 是不连通的,则其补图是连通图
证明:因图 是不连通,故 中至少有两个分支
设 是 的任意两个顶点
- 若 和 在 中不邻接,则在补图中它们邻接
- 若 和 在 中邻接,则它们属于 的同一分支,在另一个分支中取一点 ,则在补图中 和 均与 邻接,从而 是一条途径,故在补图中 和 连通
因此 的补图是连通图
定理 8:设图 为 阶简单图,若 中任意两个不相邻顶点 与 满足 ,则 是连通图且
证明:我们将证明,对 的任意两点 与 ,一定存在一条长度至多为 2 的连接 与 的路
偶图判断定理
定理 9:一个图是偶图当且仅当它不包含奇圈
证明:一个图是偶图当且仅当每个连通分支是偶图,一个圈只能属于一个连通分支,因此我们只需要对连通图证明即可
设 是具有二分类 的偶图,并且 是 的任意一个圈
不失一般性,可假定 。这样,,且
又因为 , 相邻,所以 。由此即得 是偶圈 -> 顶点是偶数,故形成边后也是偶数边
接下来证明充分性:设 是不包含奇圈的连通图
任选一个顶点 且定义 的一个分类 如下:
现在证明 是一个二分类
断言:对 中任意两点 与 ,必不相邻!! -> 如果 ,则 必为奇数
同理:对 中任意两点 与 ,必不相邻!!
所以 是 的一个二分类
赋权图
定义 24:若图 的每一条边 都附有一个实数 ,称为 的权,则 连同它边上的权称为赋权图
- 若 是一个赋权图,则 的各边权之和称为图 的权,记为
定义 25:设 是赋权图, 与 是 中两点,在连接 与 的所有路中,各边权值之和最小的路,称为 与 间的最短路,最短路的权值称为 与 的距离,仍记为
- 各边的权均为 1 的赋权图中的路长与非赋权图中的路长是一致的
最短路问题
数学模型:在一个赋权图中的两个指定顶点 和 之间找出一条最短 路
Dantzig 算法 (顶点标号法):不仅找到了最短路 路,而且还给出了 到图 的所有其他顶点的最短路
- 记 ,,,
- 若已经得到 ,且对于 ,已知 。对每一个 ,求一点:,使得:
- 设有 ,,而 使 取最小值。令:,,
- 若 ,停止;否则,记 ,转到第二步
记号说明:
- :边 的权重
- :点 的标号值,表示点 到 的最短路长度
- :已经标号的顶点集合
- : 到 的最短路上的边所在的集合
- :与点 相邻的所有点的集合,称为 的邻集
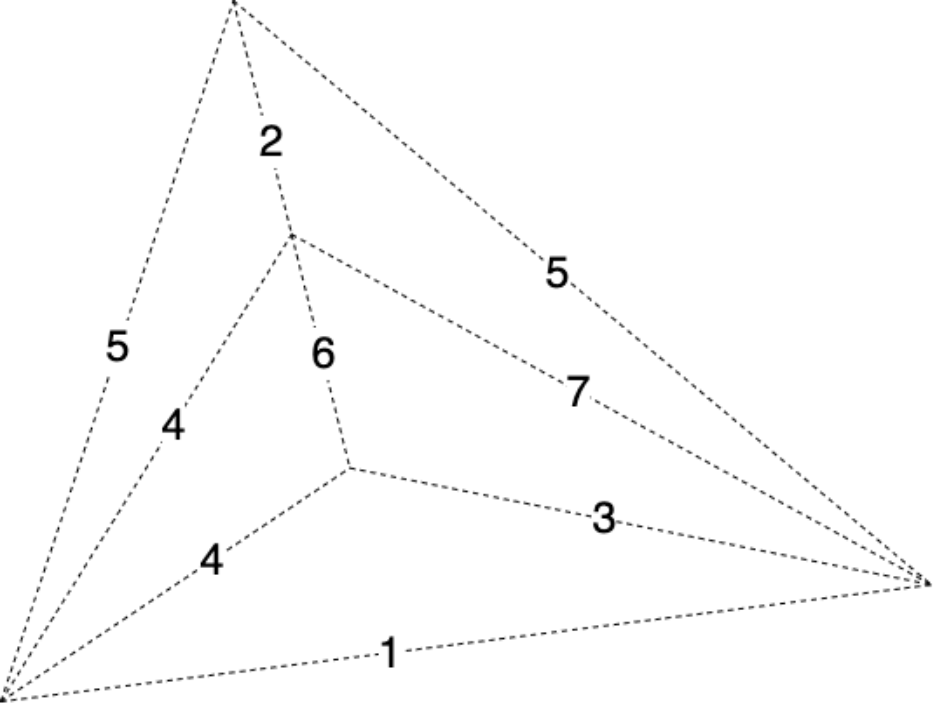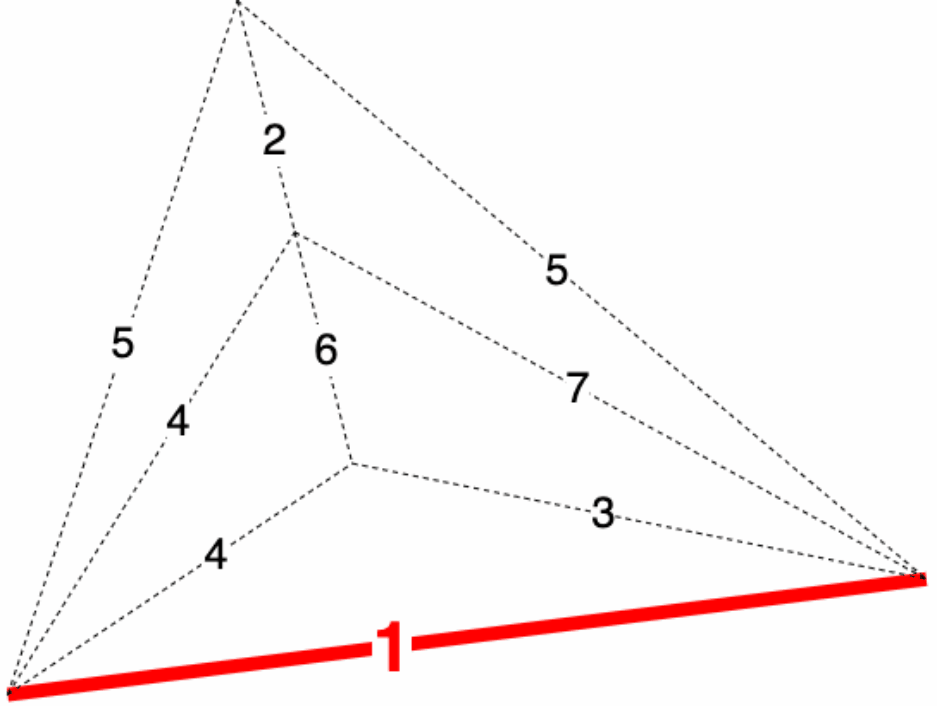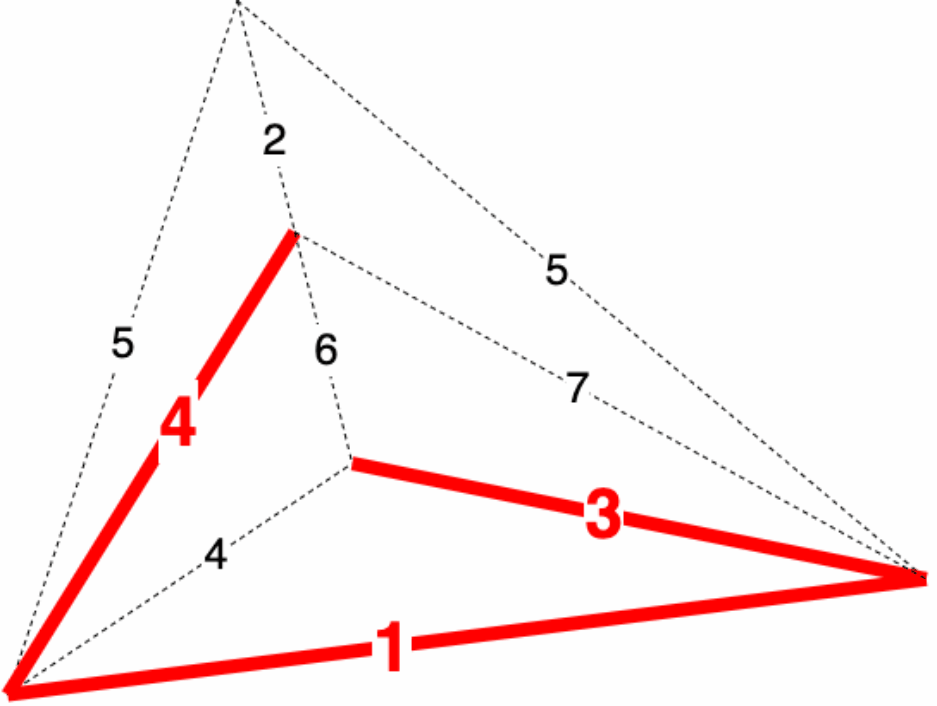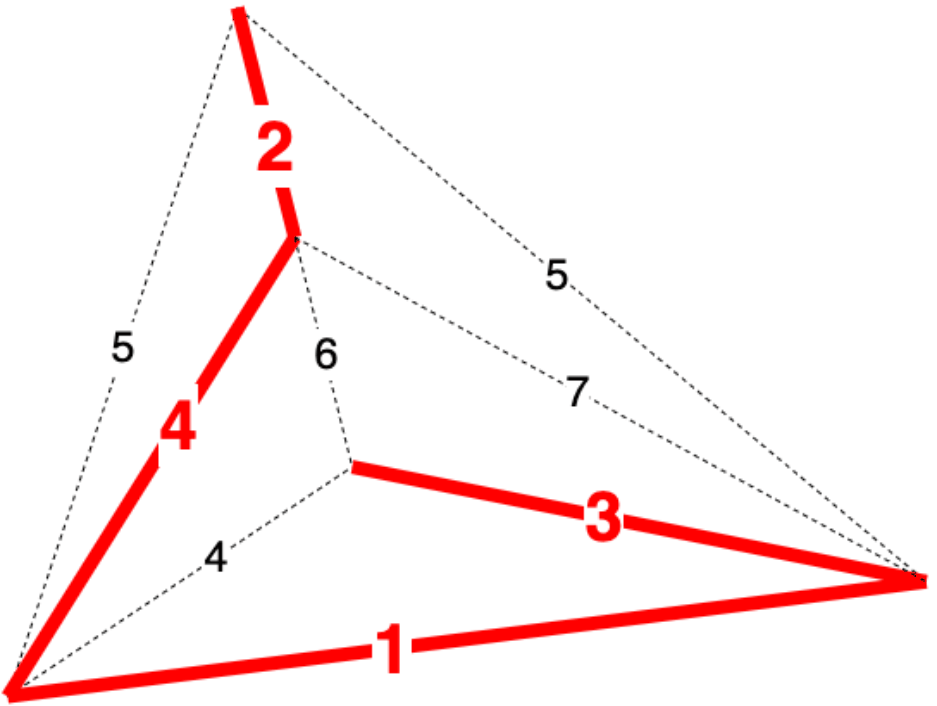
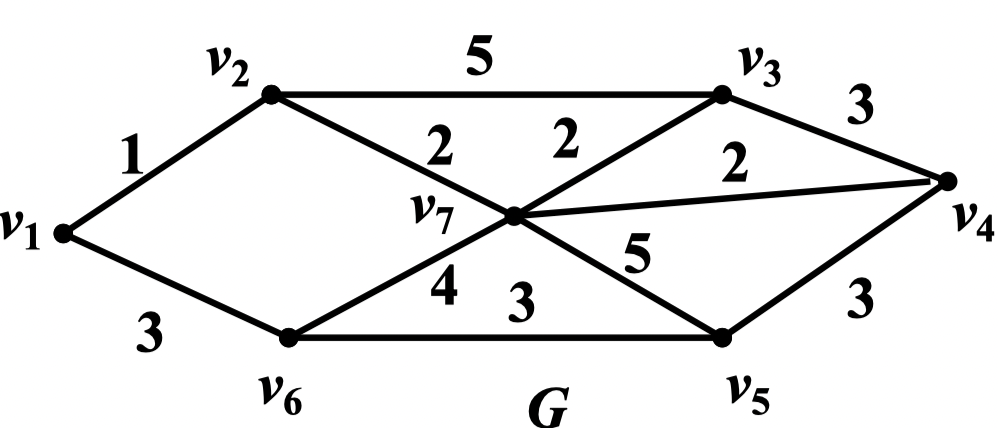
例:如图所示,求点 到点 的距离
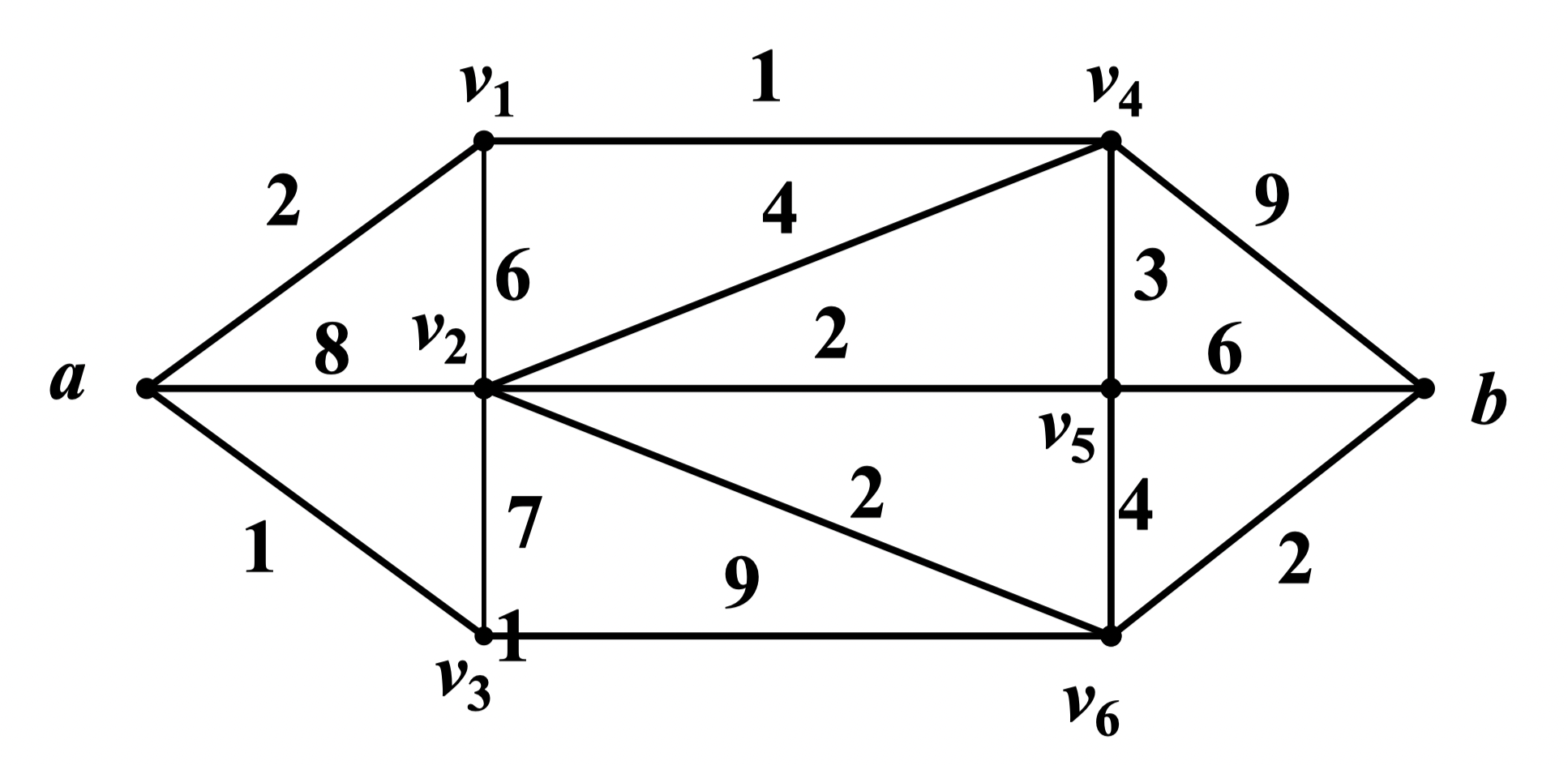
解:,,,
- 当 时,,,,
- ,,,
,
- 当 时,,,,
- 当 时,,,,
- ,,,
,
- 当 时,,,,
- 当 时,,,,
- 当 时,,,,
- ,,,
,
- 当 时,,,,
- 当 时,,,,
- 当 时,,,,
- 当 时,,,,
- ,,,
,
- ,,,,
- ,,,
,
- ,,,,,
- ,,,
,
- ,,,,,,
- ,,,
于是可知 与 的距离 ,最短路为:
邻接矩阵
定义 26:设 阶标定图 ,,则 的邻接矩阵是一个 矩阵 (简记为 ),其中若 邻接 ,则 ;否则
- 注:若 取为连接 与 的边的数目,则称 为 推广的邻接矩阵
邻接矩阵的性质
邻接矩阵是一个对称方阵
简单标定图的领结矩阵的各行(列)元素之和是该行(列)对应的点的度
若 和 是对应于同一个图的两种不同的标定的邻接矩阵,则 和 是相似的,即存在一个可逆矩阵 使得
是连通的当且仅当没有 的点的一种标定法使它的邻接矩阵有约化的形式
例:
- 到 的长为 2 的途径的数目为 1
- 到 的长为 2 的途径的数目为 0
- 到 的长为 2 的途径的数目为 2
- 到 的长为 2 的途径的数目为 0
- 到 的长为 2 的途径的数目为 5
定理 10:令 是一个有推广邻接矩阵 的 阶标定图,则 的 行 列元素 等于由 到 的长度为 的途径的数目
证明:
推论:设 为简单图 的邻接矩阵,则:
- 的元素 是 的度数。 的元素 是含 的三角形的数目的两倍
- 若 是连通的,对于 , 与 之间的距离是使 的 的最小整数
关联矩阵
定义 27:无环图 的关联矩阵 (简记为 ) 是一个 矩阵,当点 与边 关联时 ,否则
- 关联矩阵的每列和为 2;其每行的和为对应顶点的度数
邻接谱
定义 28:图 的邻接矩阵 的特征多项式:,称为图 的特征多项式
定义 29:图 的特征多项式的特征值及其重数,称为图 的邻接谱,简称谱,记为
例:求 的谱
解: 的邻接矩阵为:
计算得:
因此:
小笔记:
特征值:使 时, 的取值
重数: 不同值出现的次数
:第一行是特征值;第二行是重数
例:若两个非同构的图具有相同的谱,则称它们是同谱图。求证:下面两图是同谱图
解: 与 显然不同构
通过直接计算得:
所以 与 是同谱图
????????????????????
例:设简单图 的谱为 ,则:
证明:因 的各特征值的平方组成矩阵 的特征值,所以
又因为 的对角线元素和为
因此
例:设 是简单图 的任意特征值,则:
证明:
图的邻接代数
定义 30:设 是简单图 的邻接矩阵,容易验证 ,对于矩阵的加法和数与矩阵的乘法来说构成复数域 上的向量空间,称该空间为图 的邻接代数
- 具有 个点的路的直径显然为 ,因此 点路的邻接代数的维数为
- 点路的不同特征值的个数为 。完全图 的直径显然为 1,不同特征值的个数恰好为 2
定理 11:设 为 阶简单连通图,则
证明:
定理 12:设 为 阶简单连通图,则 的不同特征值的个数 满足不等式
证明:
图空间 (几乎不考)
具有 条边的简单标号图的生成子图的个数显然为
设 表示简单图 的全部生成子图
定理 13:集合 在对称差运算 与数乘运算 , 下,构成数域 上的一个 维向量空间
l 部图的概念与特征
定义 31:若简单图 的点集 有一个划分:,, 且所有的 非空, 内的点均不邻接,称 是一个 部图
- 如果 ,则 就是偶图
- 阶无环图必是 部图
- 若 ,则任意的 部图也是 部图
例:
定义 32:如果在一个 部图 中,,任何两点 ,,, 均邻接,则称 为完全 部图。记作
- 完全 部图也可表示为
- 完全 部图 的点数: 边数:
- 任意部的点和其他部的所有点均相连
例:
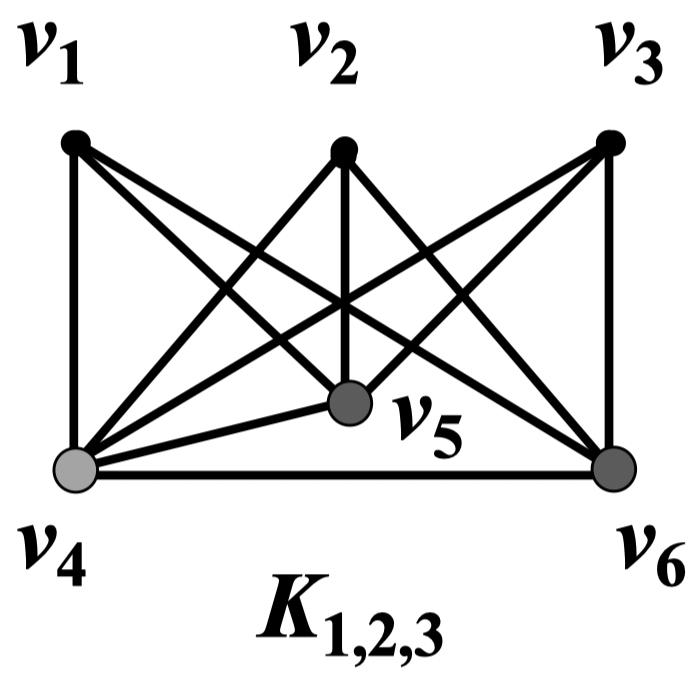
定义 33:如果在一个 阶完全 部图 中,,,则称 为 阶完全 几乎等部图,记作
- 的完全 几乎等部图称为完全 等部图
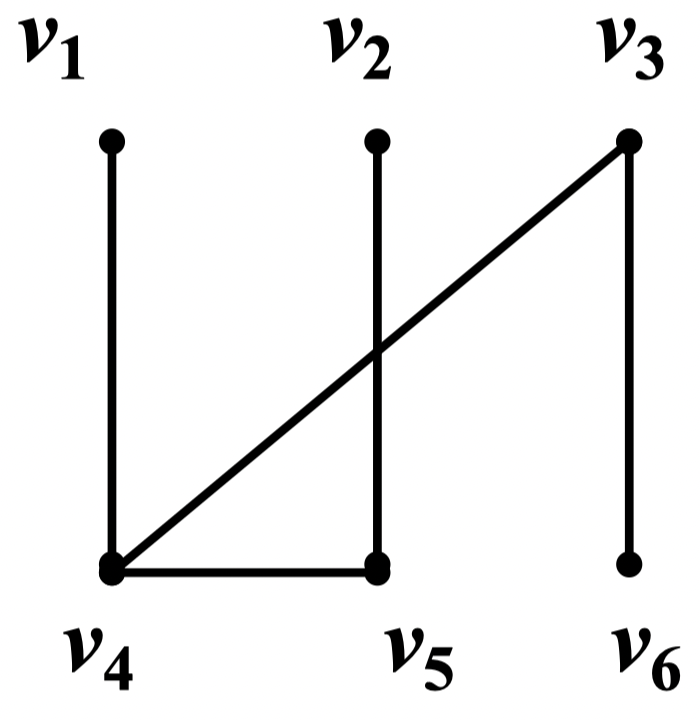
- 这是一个连通的 3 部图,点集 的划分为 ,,
- 的划分也可为 ,,
- 这也是一个 2 部图,点集的划分为 ,,且划分唯一
定理 14:连通偶图的 2 部划分是唯一的
证明:
定理 15: 阶完全偶图 的边数 ,且
证明:
定理 16: 阶 部图 有最多边数的充要条件是
证明:
Turán 定理
定义 34:设 和 是两个 阶图,称 度弱于 ,如果存在双射 ,使得对任何点 ,有
- 若 度弱于 ,一定有:。但逆命题不成立。
- 例:(1,1,2,4)与(3,3,3,3)没有度弱关系!
定理 17:若 阶简单图 不包含 ,则 度弱于某个完全 部图 ,且若 具有与 相同的度序列,则
定理 18 (Turán):若 是 阶简单图,并且不包含 ,则边数 。此外,仅当 时,
,则
例: 阶简单图 ,,则 最多有 条边
例: 9 阶简单图 ,,则 最多有 27 条边
Turán 定理应用
工兵排雷问题:一个由 个人组成的小组在一个平原地区执行一项排雷任务。对于其中任意两个人,若其距离不超过 米,则可用无线电保持联系;若发生触雷意外,地雷的杀伤半径为 米。问:在任意的两个人之间均能保持联系的条件下,若发生意外,平均伤亡人数最低的可能值为多少?
定理 19:设 为任意一个直径为 1 的平面点集,则 中距离大于 的点对的最大数目为 。并且对每个点 ,存在直径为 1 的点集 ,它恰有 个点对,其距离大于
第二章 树
树的概念
定义 35:不含圈的图称为无圈图,连通的无圈图称为树。树常用符号 表示
定义 36:无圈图称为森林
 注意
注意
- 树与森林都是简单图
- 树与森林都是偶图 -> 定理 9
- 在一棵树中,度数为 1 的顶点称为树叶,度数大于 1 的顶点称为分支点
树的性质
定理 20:每棵非平凡树至少有两片树叶
定理 21:设 是具有 个点 条边的图,则下列命题等价:
- 是树
- 无环且任意两个不同点之间存在唯一的路
- 连通,删去任一边便不连通
- 连通,且
- 无圈,且
- 无圈,添加任何一条边可得唯一的圈
 注意
注意
- 树是含有边数最少的连通图,因此树也被称为最小连通图
- 树是含有边数最多的无圈图
推论:假定 图 是由 颗树组成的森林,则
证明:设 的每棵树的点数与边数分别是 和
则 ,
因此:
例:设 是树且最大度为 ,则 至少有 片叶子
证明:若不然,设 有 个顶点, 条边且至多 片叶子
由握手定理得:
所以, 与 是树矛盾!
例:设 为具有 12 条边的树,其顶点度的取值为 1,2,5。如果 恰好有 3 个度为 2 的顶点,那么 有多少片树叶?
解:设 有 片树叶,根据树的点数与边数的关系和, 有 13 个顶点
由握手定理得:
得:,即 有 8 片树叶
练习:设树 中度数为 的顶点的个数为 ,则
证明:
例:设 是森林且恰有 个奇度顶点,则在 中有 条边不重合的路 ,使得:
证明:
例:证明:单调不增正整数序列 是一棵非平凡树的度序列当且仅当
证明:
例:设 是 阶树,证明:若简单图 满足 ,则 同构于 的某个子图
证明:对 作归纳证明
树的中心
定义 37:设 是一连通图,,令 ,则称 为顶点 的离心率;又令 ,称 为图 的半径
定义 38:若对一个点 ,,称 为 的一个中心点, 的全体中心点构成的集合称为 的中心
例:在下图所示的树中,图中每个顶点处标出的数字表示该点的离心率,图中的顶点 为该树的中心,该树的半径 ,直径 。在该图中,树的中心是点
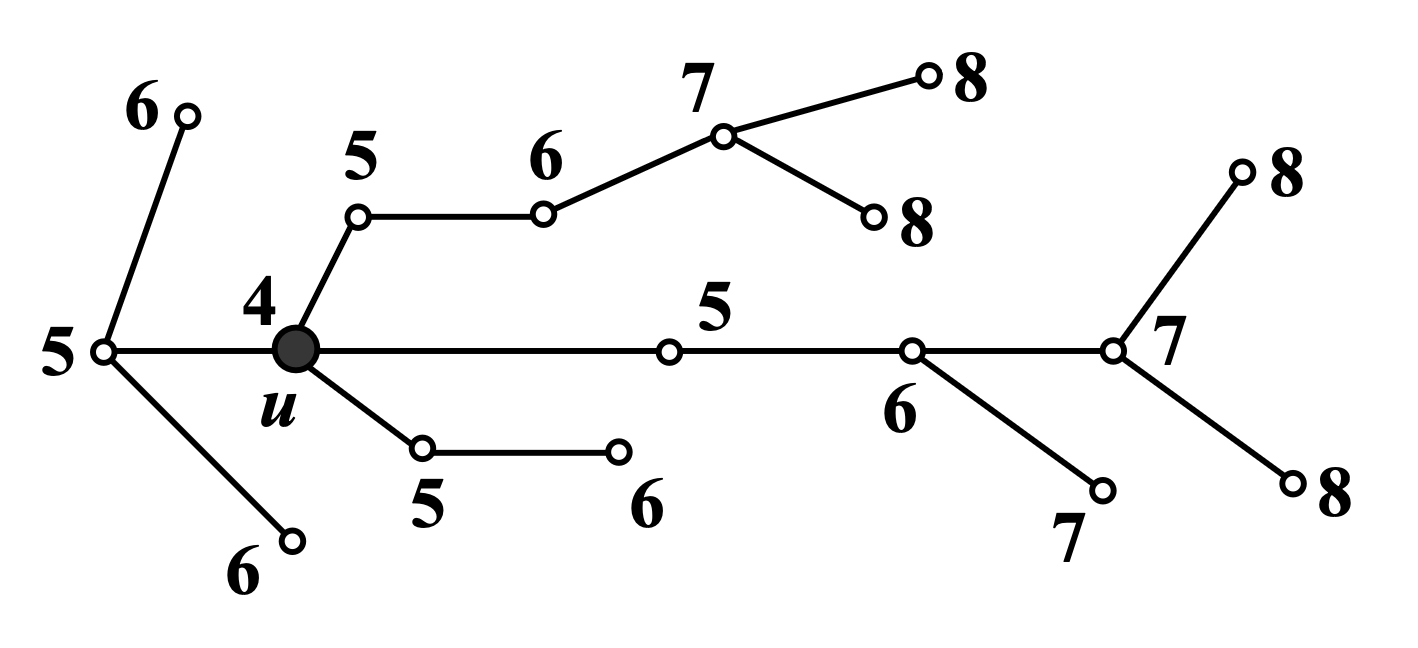
定理 22:每棵树的中心由一个点或两个相邻点组成
证明:对树 的阶数 作归纳证明
当 或 时,结论显然成立
...
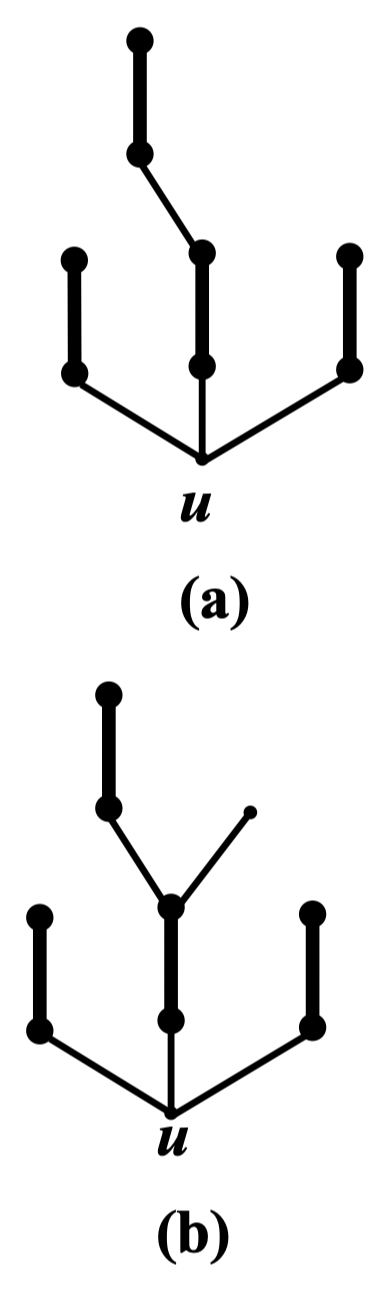
树的形心
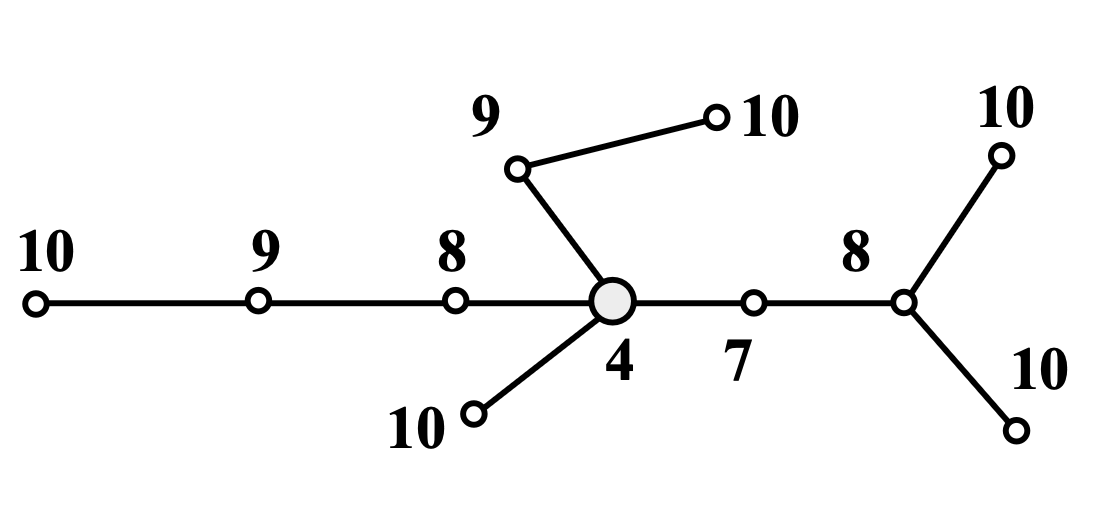
定义 39:设 是树, 是树 的任意一个顶点,树 在点 处的一个分枝是指包含 作为一个叶子点的极大子树,其分枝数为该顶点的度数;树 在点 的分枝中边的最大数目称为点 的权;树 中权值最小的点称为它的一个形心点,全体形心点的集合称为树 的形心
例:在右图树中,每个顶点处的数字表示该顶点的权值,权值为 4 的顶点为该树的形心
定理 23:
- 每棵 阶树 的形心由一个点或两个相邻点组成
- 若 只有一个形心点,则形心点的权小于
- 若 有两个形心点,则形心点的权均为
证明:
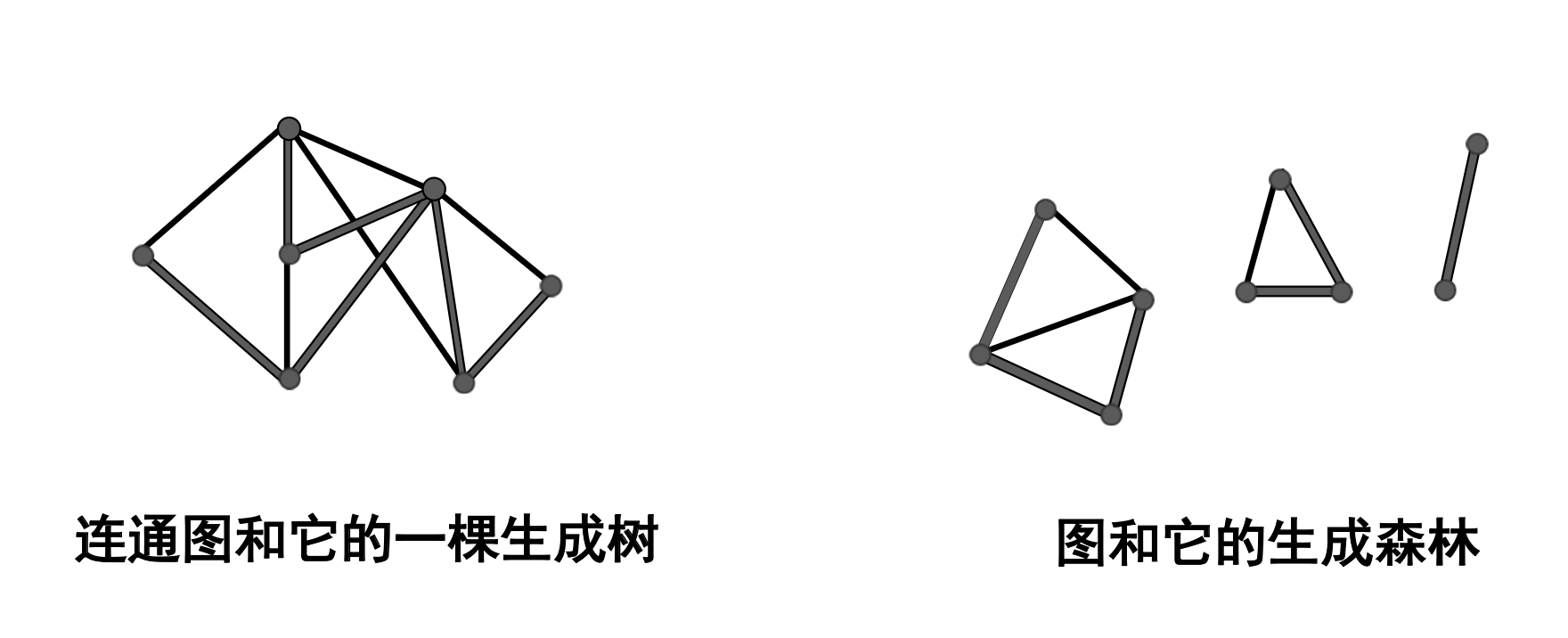
生成树的概念 & 性质
定义 40:若图 的生成子图 是树,则称 为 的生成树;若 为森林,称它是 的生成森林。生成树的边称为树枝, 中非生成树的边称为弦
例:
定理 24:每个连通图至少包含一颗生成树
推论:若 是 连通图,则
树是最小连通图,存在关系
所以如果是图的话,必满足
生成树的计数
 注:以下讨论的生成树的个数均指标定图而言。标定图的生成树的数量远大于非标定图生成树的数量。如标定图 有 棵生成树,而不同构的 6 阶树仅 6 棵
注:以下讨论的生成树的个数均指标定图而言。标定图的生成树的数量远大于非标定图生成树的数量。如标定图 有 棵生成树,而不同构的 6 阶树仅 6 棵
定义 41: 的边 称为被收缩,是指删去边 并使它的两个端点重合,如此得到的图记为
- 注: -> 团数
- 若 是树,则 也是树
例:下图 表示图 收缩边 后得到的图
用 表示 的生成树的个数
定理 25 (Cayley):若 是图 的边,则:
证明:由于 的每一棵不包含 的生成树也是 的生成树
由此推知, 就是 不包含 的生成树的个数
类似的, 就是 的包含 的生成树的个数
- 理解:因为收缩了边 ,故当经过收缩顶点时,还原到原图中,即经过了边
例:对右图 ,计算
解:
所以,
定理 26 (矩阵树定理):设无环连通图 的顶点集合为 , 是 的推广的邻接矩阵, 是 阶方阵,其中:
则 的生成树的个数为 的任意一个余子式的值
例:图 如图所示。求
解:
记 删去第 行及第 列后得到的矩阵为 ,则:
所以:
定理 27:
证明一:显然
记 删去第 行及第 列后得到的矩阵为 ,则:
所以
证明二:设 的顶点集是
由 中的元素组成的长为 的序列的个数为
接下来,我们将在 的生成树的集合与这种序列的集合之间建立一一对应
假定 是 的一棵生成树,设 是 中标号最小的叶子点,把与 相邻的顶点的标号记为
现在从 中删去 ,用 表示 中标号最小的叶子点,把与 相邻的顶点的标号记为
重复这一过程,直到得到
很容易看出,最后剩下一条边
上述逆过程:
- 中任意一顶点 在序列 中出现 次,故 中的 度顶点恰好是在该序列中未出现的那些顶点
- 每次都在 中找未在 中出现的第一个顶点,与 相连,同时分别在 和 中划掉该顶点和
- 重复上述步骤,直到确定了 条边,即 为空
- 最后连接 中剩余的两个顶点
回路系统简介
定义 42:设 是图 的一棵生成树, 和 分别是 的边数与顶点数, 为 的弦,设 是 加 产生的圈 ,称 为对应于弦 的基本回路, 称为对应于生成树 的基本回路系统
例: 为 的一棵生成树,求所有基本回路
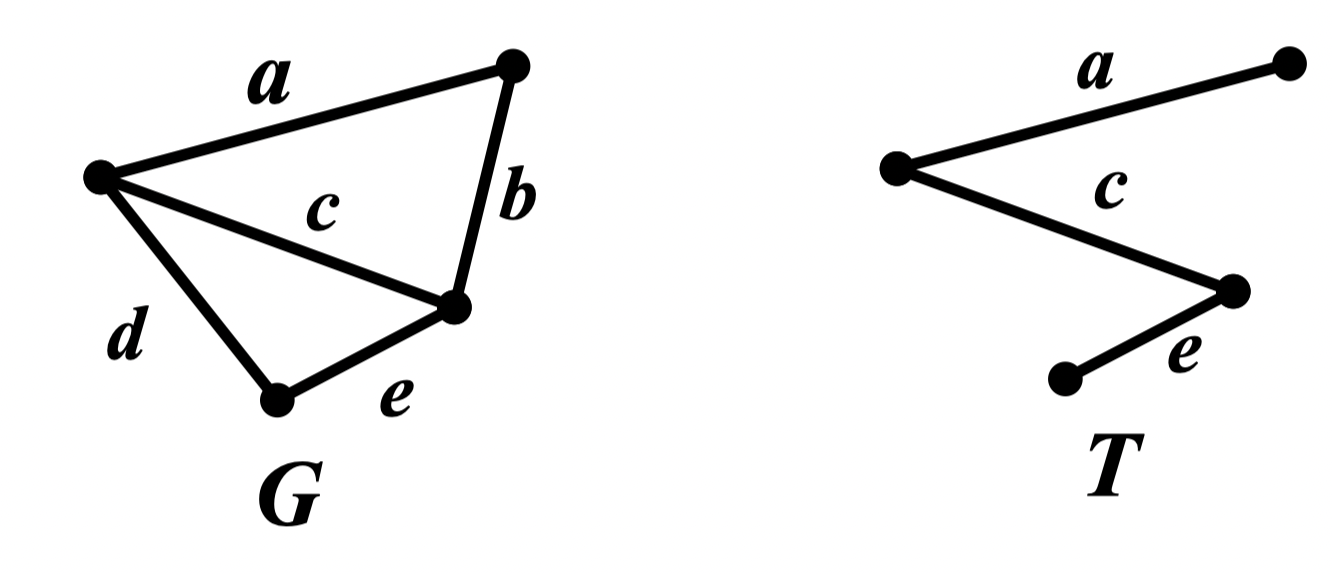
解:基本回路为:
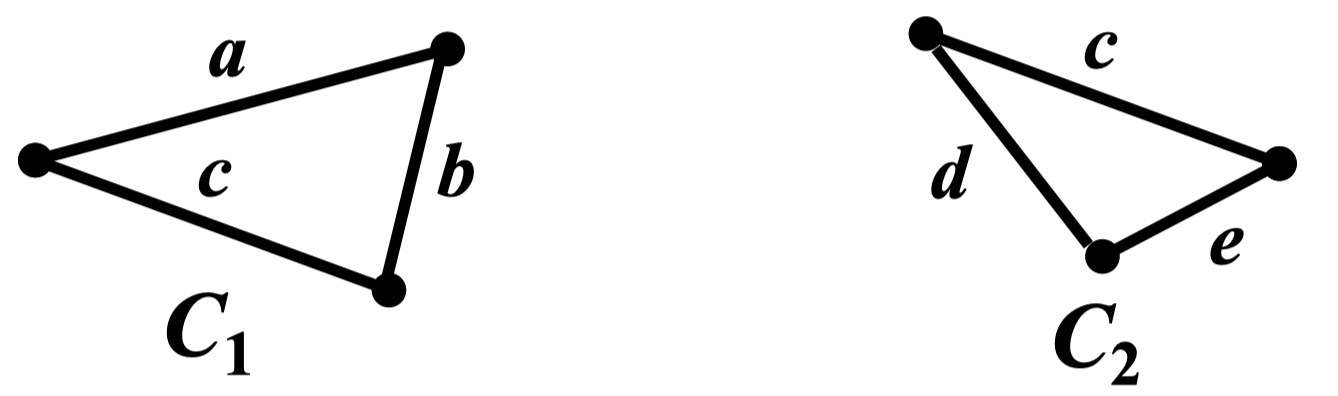
定理 28:连通图 的任一回路均可表示成若干个基本回路的对称差 -> 对称差 click
Kruskal 算法
定义 43:在连通赋权图 中,边权之和最小的生成树称为 的最小生成树
Kruskal 算法
选择边 使得其权值最小
若已经选定边 ,则从 中选择边 ,使得:
- 为无圈图
- 的权值尽可能小
当步骤 2 不能进行时,停止
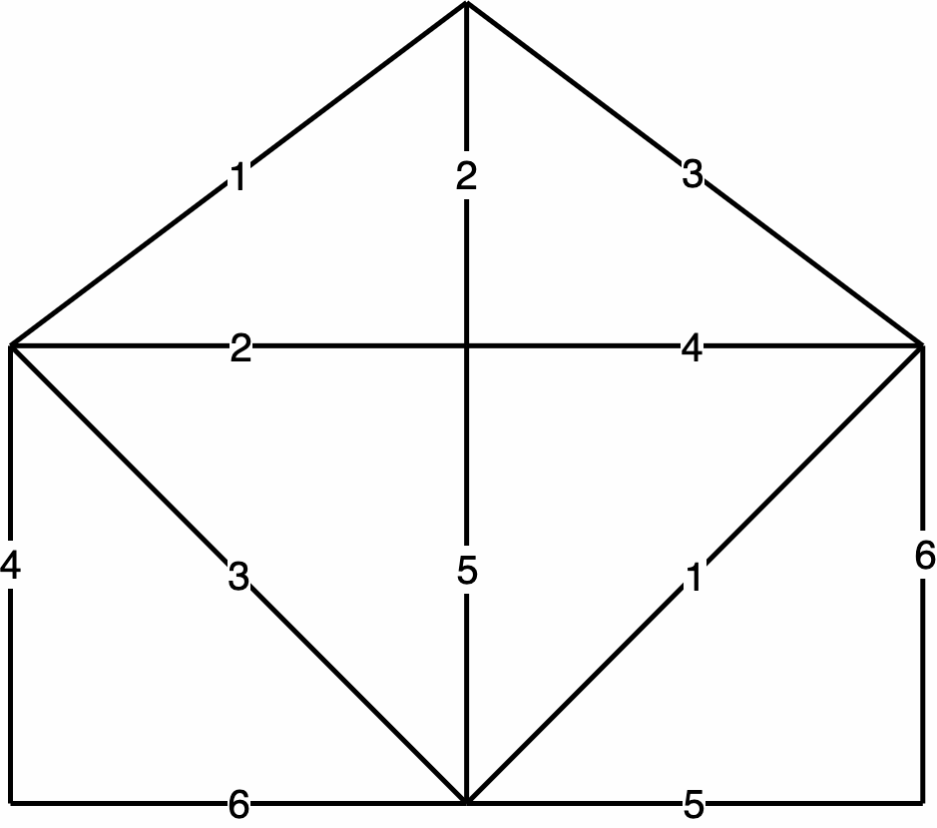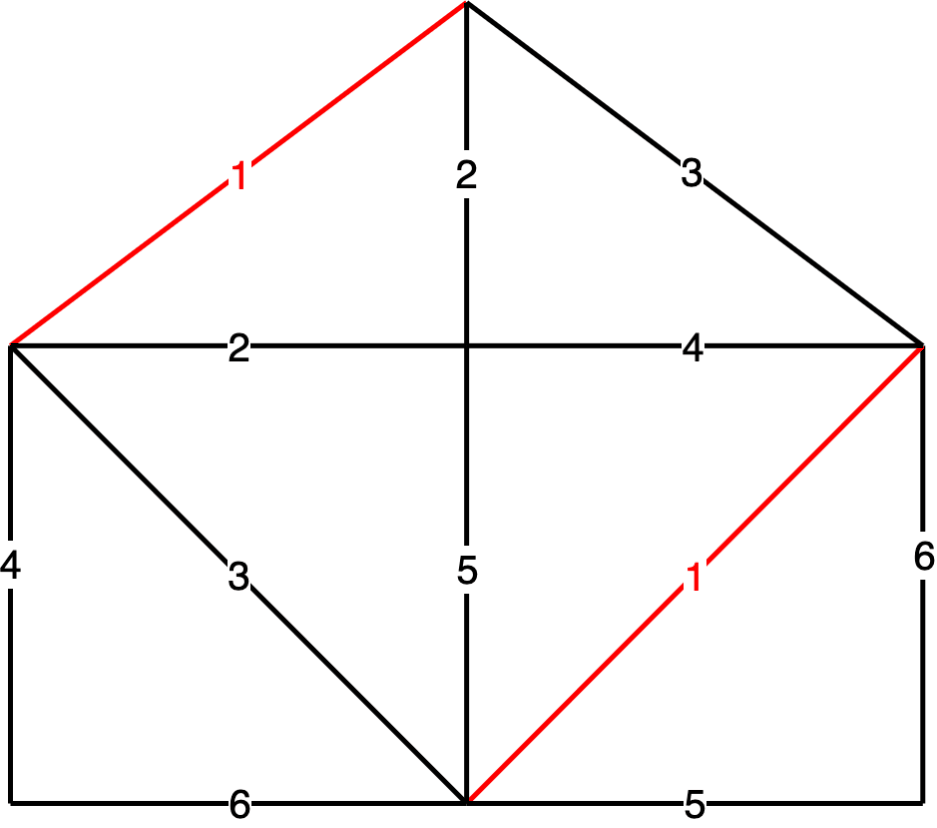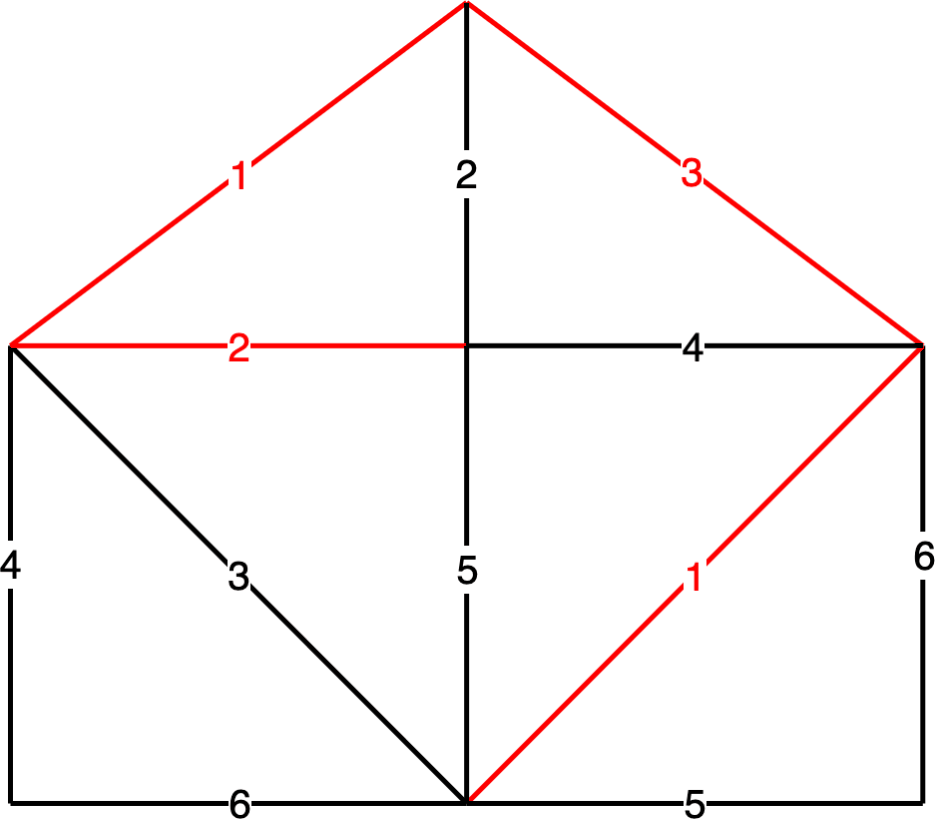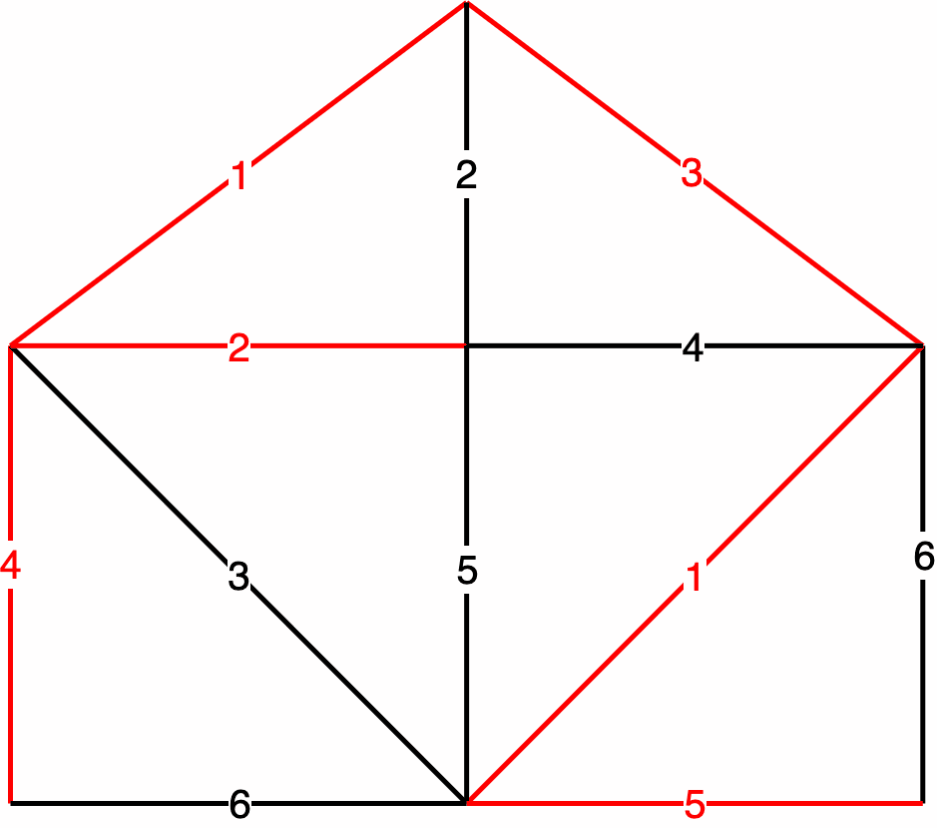
例:求 的最小生成树
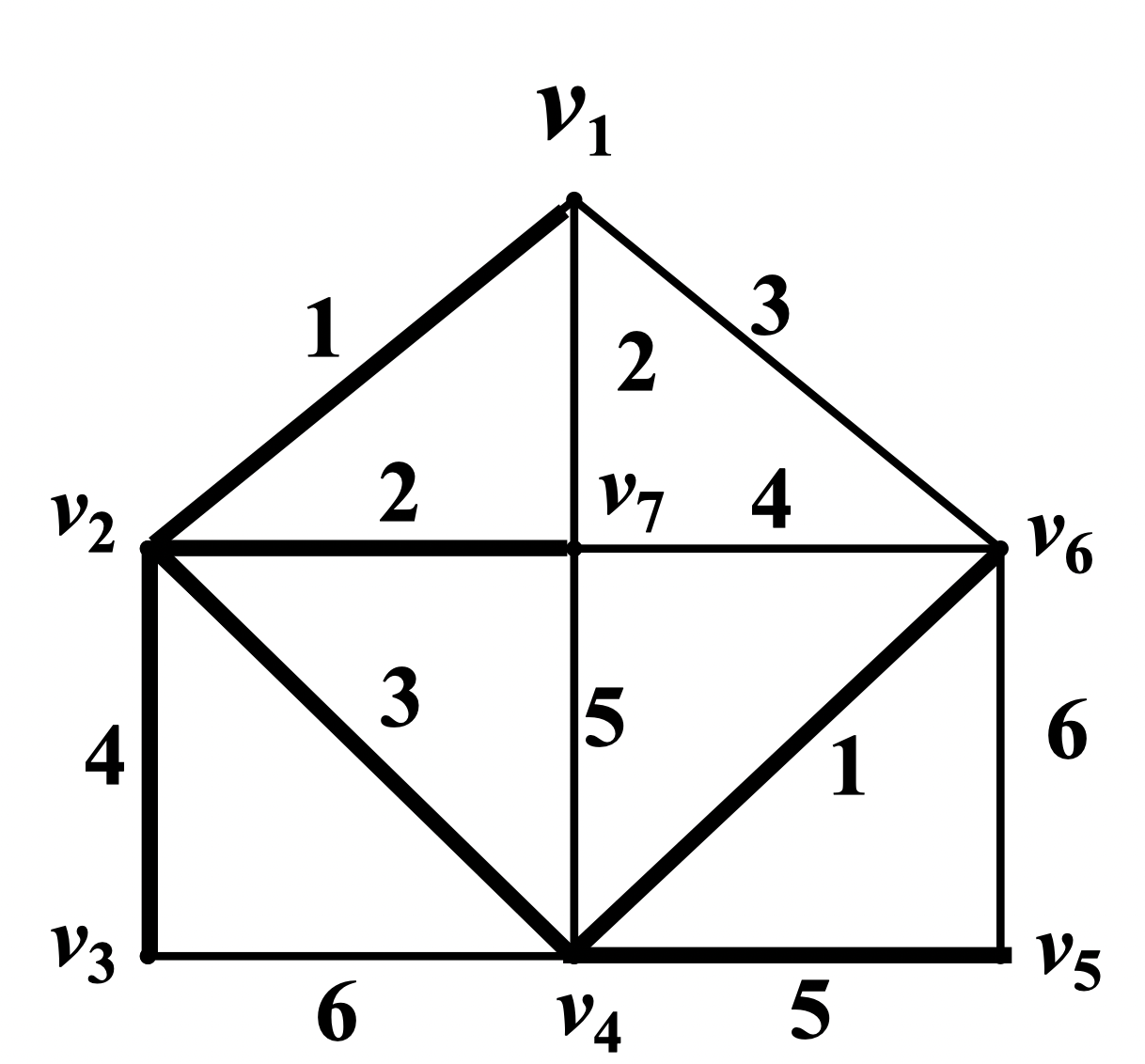
解:依据算法,粗线的边为依次被选为生成树 的边,且
破圈法
- 从赋权图 的任意圈开始,去掉该圈中权值最大的一条边,称之为破圈
- 不断破环圈,直到 中没有圈为止
- 最后剩下的 的子图为 的最小生成树
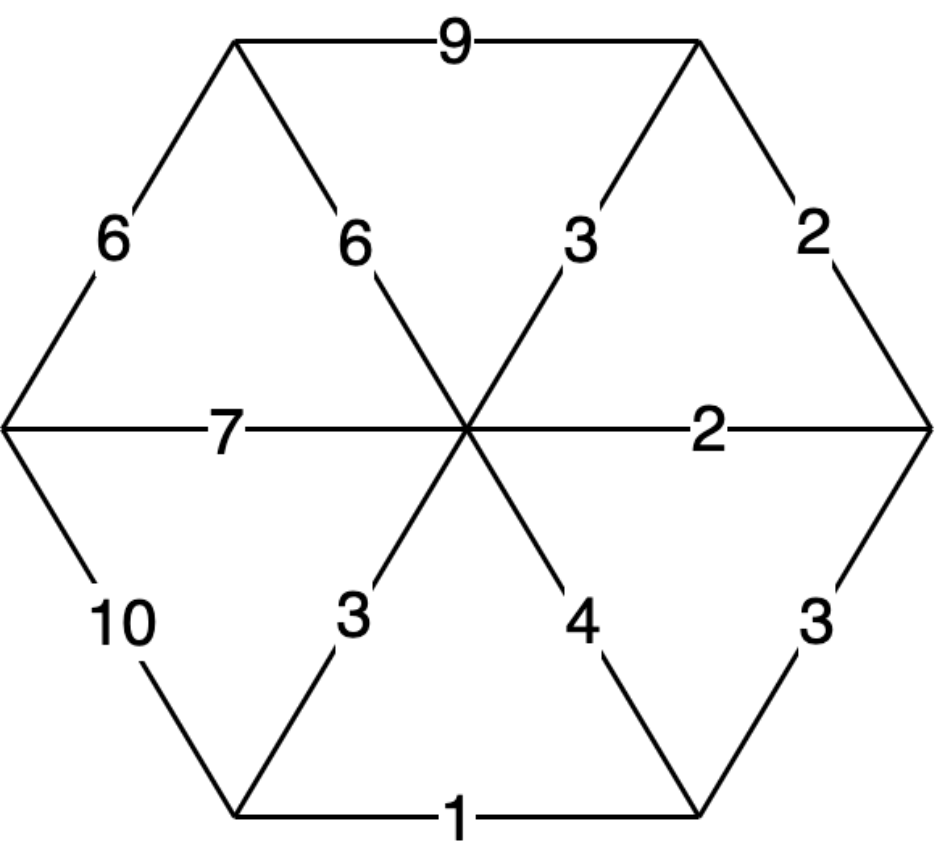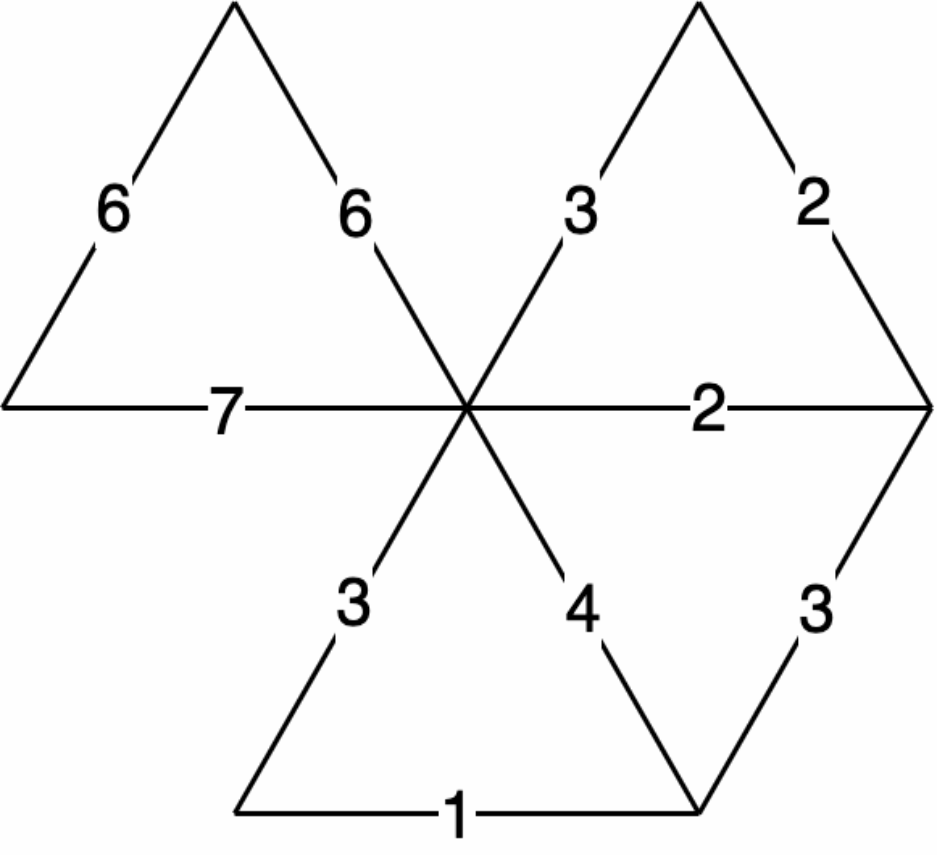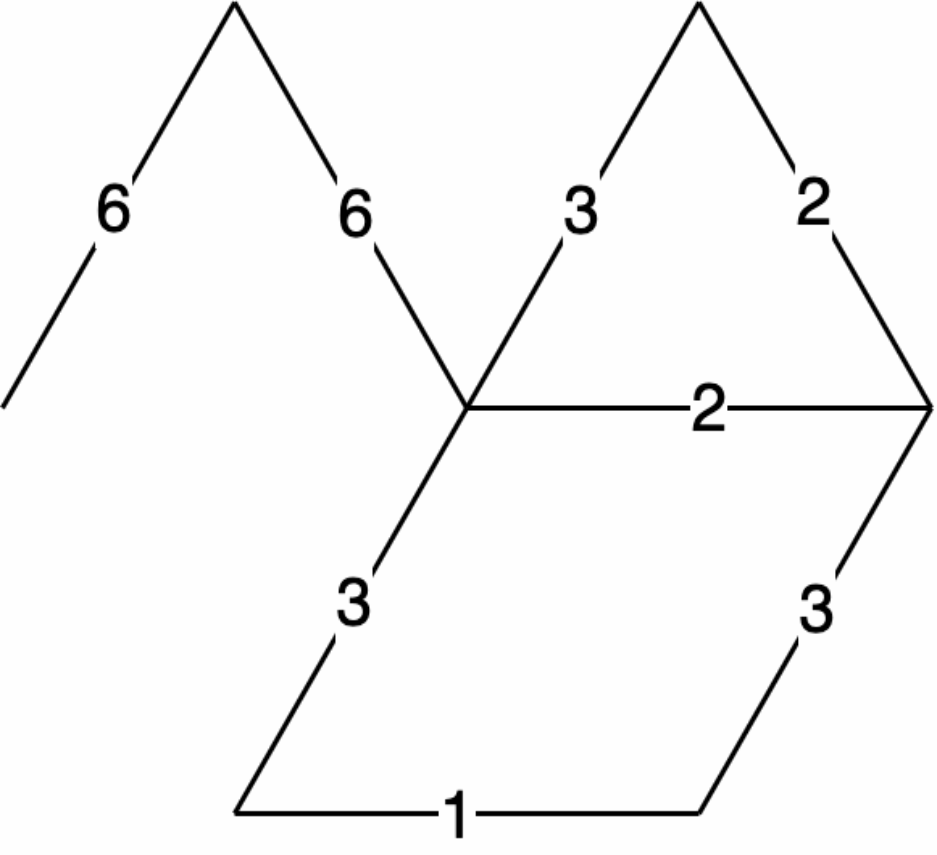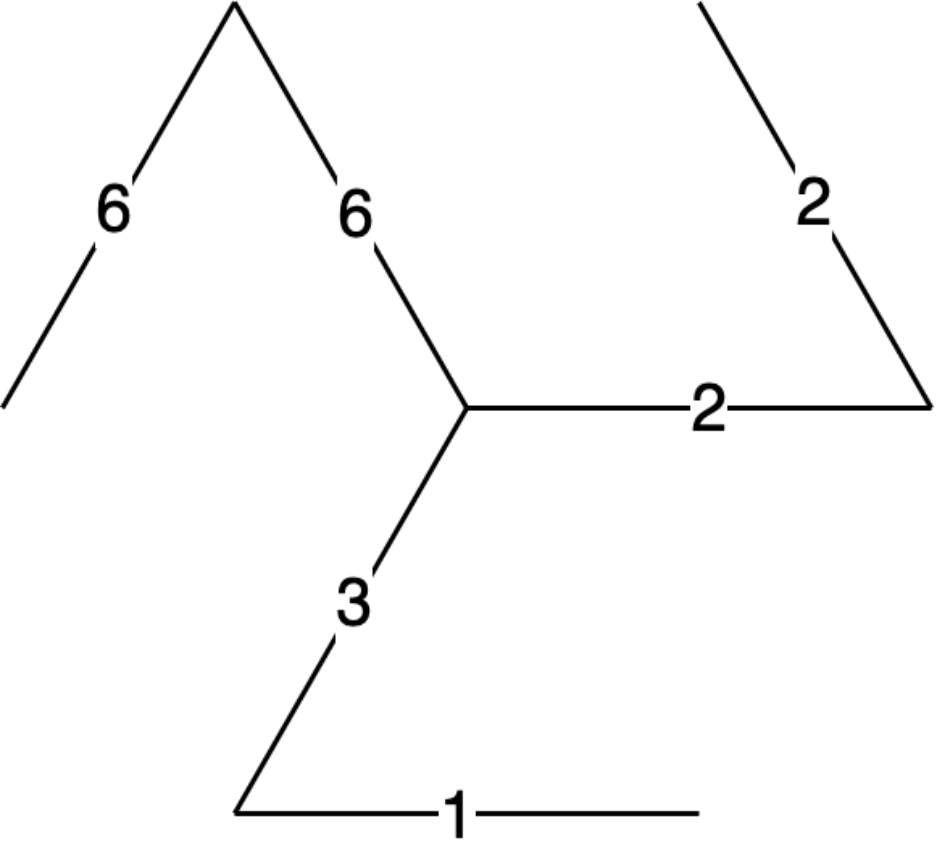
例:利用破圈法求下图 最小生成树
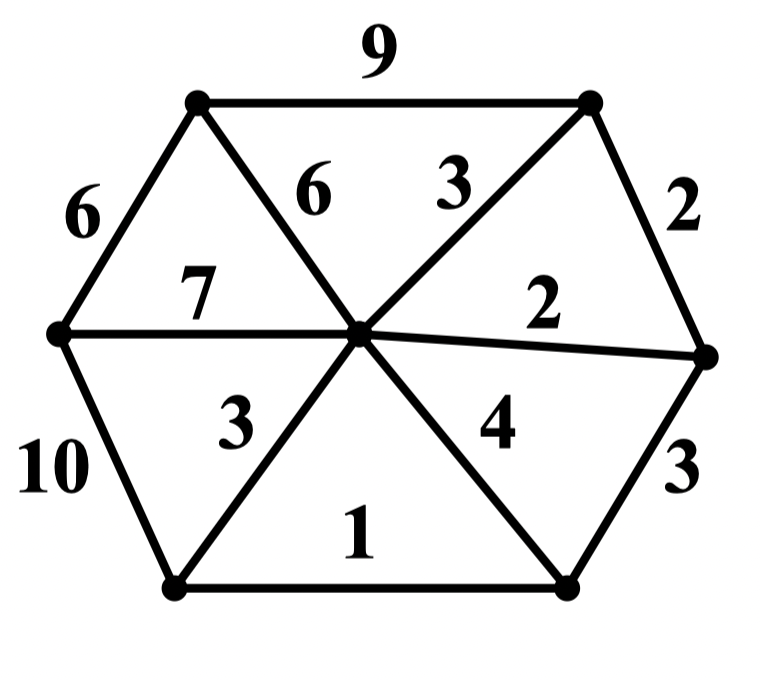
解:过程如图所示
Prim 算法
- 对于连通赋权图 的任意一个顶点 ,选择与点 关联的且权值最小的边作为最小生成树的第一条边
- 在与一条已经选取的边只有一个公共端点的所有边中,选择权值最小的边
- 重复步骤 2 直至得到一棵生成树
例:用 Pirm 算法求下图的最小生成树
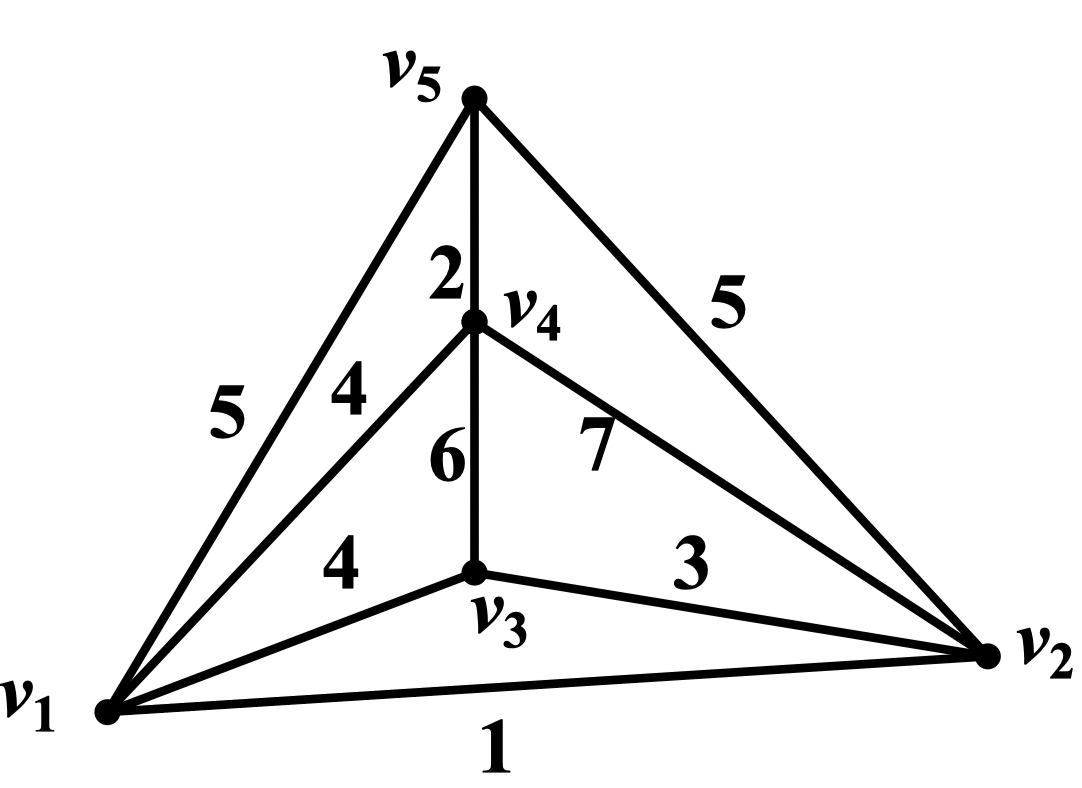
解:过程如图所示
第三章 图的连通度
割边及其性质
定义 44:设 是图的一条边,若 ,则称 为 的割边
 注:若 连通,则割边是指删去后使 不连通的边,故非平凡树的每条边均为割边
注:若 连通,则割边是指删去后使 不连通的边,故非平凡树的每条边均为割边
例:下图中,边 和 为割边,而其余边均不为割边
定理 29: 是图 的割边当且仅当 不在 的任何圈中
证明:因结论若在 的含 的连通分支中成立,则必在 中成立,所以我们不妨假定 连通
必要性:设 是图 的割边,若 含在圈 中,令 。易知 是 中一条 路
任取 中两个不同点 和 ,因 连通,故 中存在 路
- 若 不含 ,则 也是 中一条 路
- 若 含 ,用 替换 后也可得到 中一条 路,以上表明 连通,这与 是割边矛盾,所以 不在 的任何圈中
充分性:设 ,若 不是 的割边,则 仍连通,从而在 中存在 路 ,这样 便是 中含 的圈,这与假设 “ 不在 的任何圈中” 矛盾!
所以, 是 的割边
 注:以上定理表明圈中的边一定不是割边,所以删去圈中的边不会破坏图的连通性
注:以上定理表明圈中的边一定不是割边,所以删去圈中的边不会破坏图的连通性
推论:设 是连通图 的任意一条边,若 含在 的某圈中,则 仍连通
例:求证:
- 若 的每个顶点的度数均为偶数,则 没有割边
- 若 为 正则二部图 ,则 无割边
证明:(1)若不然,设 为 的割边
则 的含有顶点 的那个分支中点 的度数必为奇数,而其余点的度数为偶数,与 “度数为奇数的顶点的个数为偶数” 矛盾!
(2)若不然,设 为 的割边
假设 为 的包含顶点 的连通分支,显然 中除了点 的度数为 外,其余点的度数均为
显然 仍为偶图,设其二部划分为 和 且 ,
不妨假设 包含顶点 ,则
但是因 ,所以等式不能成立!因此, 一定不是割边
- 解释:,其中 为整数,
- 故等式不可能成立
割点及其性质
定义 45:图 的顶点 称为割点,如果 可划分为两个非空子集 和 ,使得 和 恰有一个公共顶点
 注意
注意
- 若 ,则 必为 的割点
- 若 无环,则 是 的割点当且仅当
- 若无环图 连通,则割点是指删去该点使 不连通的点
- 非平凡树一定有割边,不一定有割点()
- 没有割点 没有割边()
- 有割点 有割边(八字形的图)
- 阶数 的无环连通图,有割边 有割点
- 阶数 的无环连通图,有割点 有割边
例: 图中点 是割点,其余点均不为割点
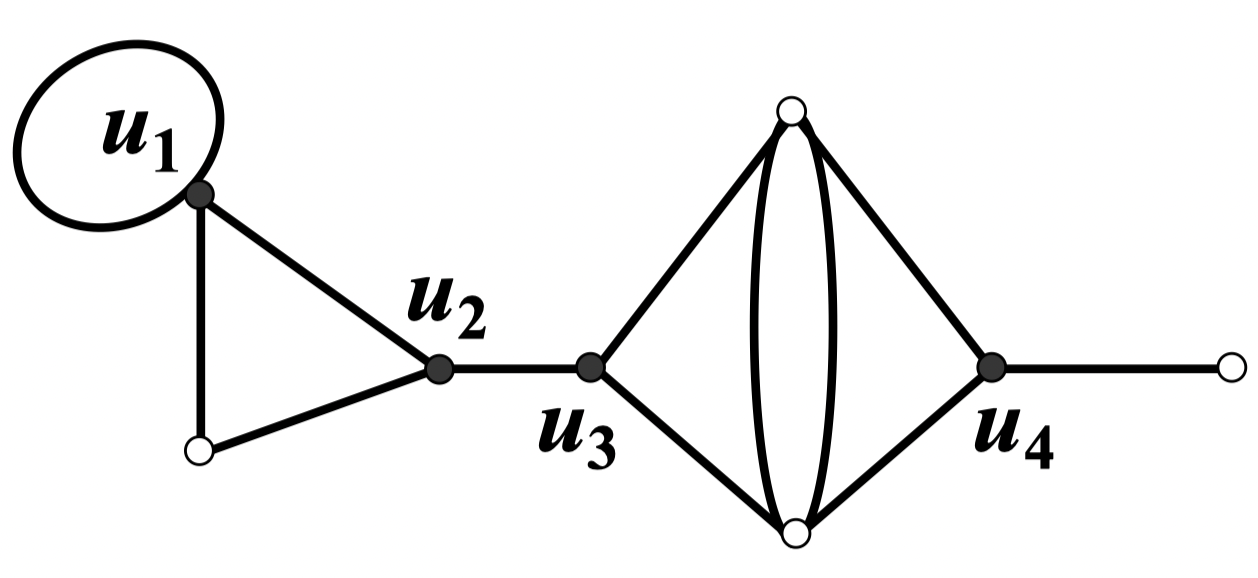
定理 30:设 是树 的顶点,则 是 的割点当且仅当
证明:必要性:若不然,有 ,即 是树叶,显然不可能是割点
充分性:设顶点 的度数大于 1
设 和 是与 相邻的两点,由树的性质知,只有唯一的路连接 和 ,所以 分离 与 。因此, 是割点
定理 31:设 是无环连通图 的一个顶点,则 是 的割点当且仅当 可划分为两个非空顶点子集 与 ,使得对任意的 ,,点 都在每一条 路上
证明:
例:求证:无环非平凡连通图至少有两个点不是割点
证明:由于 是无环非平凡连通图,所以存在非平凡生成树。
非平凡生成树至少两片树叶,它们不能为生成树的割点
显然,它们也不能为 的割点
例:求证:恰有两个非割点的连通简单图是一条路
证明:设 是 阶连通简单图 的任意一棵生成树
由于 有 个割点,所以, 有 个割点,因此 只有两片树叶,所以 是一条路
这说明, 的任意生成树为路
一个简单图的任意生成树为路,则该图为圈或路
若为圈,则 没有割点,矛盾!所以 为路
例:求证:若 是简单图 的割点,则 不是 的补图的割点
证明:容易验证,
因为 是 的割点,所以 一定不是连通图。从而 的补图是连通图
因此,在 的补图中删去顶点 不会增加图的连通分支数
所以, 不是 的补图的割点
块及其性质
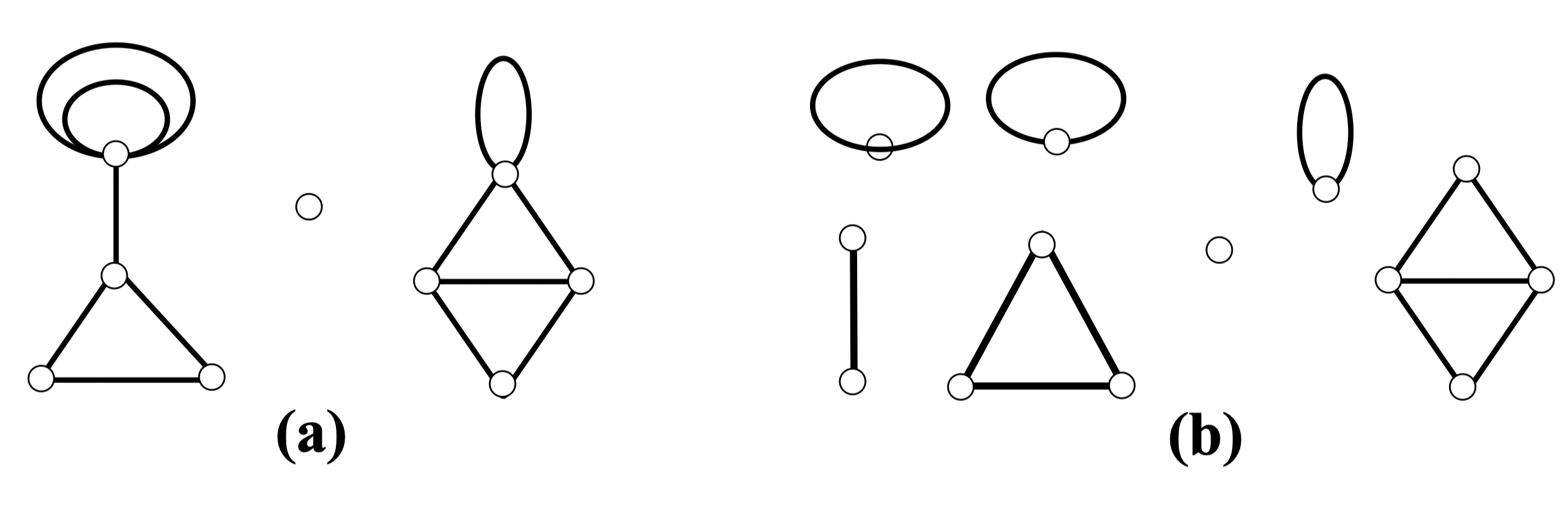
定义 46:没有割点的连通图称为块图,简称块。若图 的子图 是块,且 中没有真包含 的子图也是块,则称 是 的块
 注意
注意
- 仅有一个点的块,要么是孤立点,要么是环
- 仅有一条边的块,要么是割边,要么是环
- 至少有两个点的块无环
- 至少有三个点的块无环、无割边
例:图 如图 所示, 的所有块如图 所示
定理 32:设图 的阶至少为 ,则 是块当且仅当 无环并且任意两点都位于同一个圈上
证明:充分性:此时 显然连通
假设 是任意一点, 与 是 之外的任意两点
和 在一个圈上,说明 和 之间至少有两条不相交的路
删去 至多破坏 和 之间的一条路,说明 不是割点
又因为 无环,所以 是块
???????????????????
推论:设 的阶至少为 ,则 是块当且仅当 无孤立点且任意两条边都在同一个圈上
证明:
定理 33:点 是图 的割点当且仅当 至少属于 的两个不同的块
证明:必要性:设 是 的割点
由割点定义知 可以划分为两个边子集 与 使得 与 有唯一公共顶点
设 与 分别是 和 中包含 的块,显然它们也是 的块。因此 至少属于 的两个不同块
充分性:设点 属于 的两个不同块 和
如果 和 其中一个是环,显然 是割点
????????????????????
 注:两个不同块的公共顶点只能是割点,即块与块只能由割点相联结,因此可以通过割点搜寻块
注:两个不同块的公共顶点只能是割点,即块与块只能由割点相联结,因此可以通过割点搜寻块
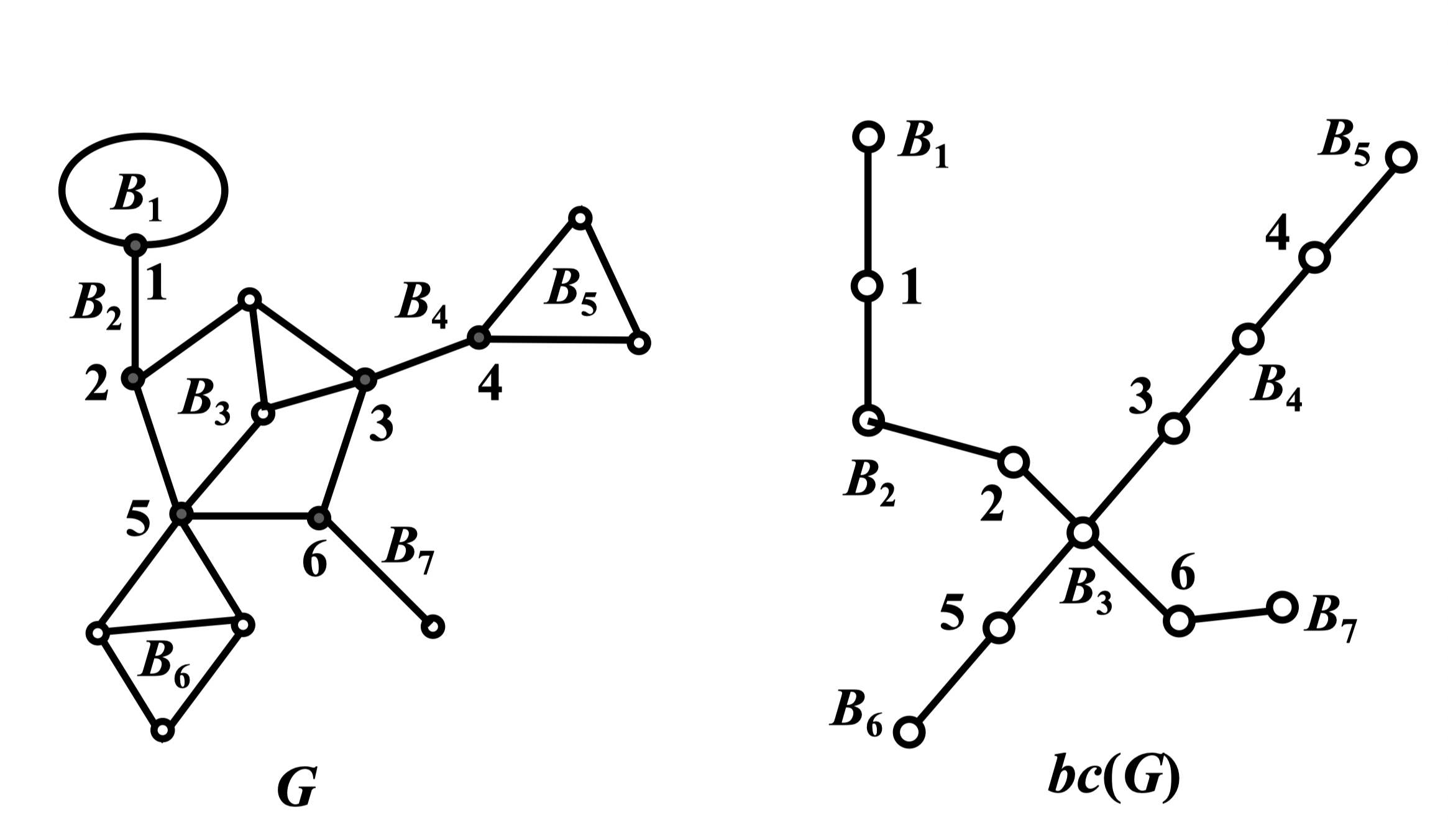
定义 47:设 是平凡连通图, 是 的全部块,而 是 的全部割点。构成 的块割点树 :它的顶点是 的块和割点, 是 的一条边当且仅当 与 中有一个是 的割点,另一个是该割点联结的块
 注意
注意
- 是一个没有圈的连通图,即为树
- 若 本身就是一个块,则 是平凡图
- 若 本身不是块,则 至少有三个点并且叶子点为 的只含一个割点的块
例:
连通度和边连通度
定义 48:给定连通图 ,设 是 的顶点子集,若 不连通,则称 为 的顶点割,含有 个顶点的顶点割称为 的 顶点割。 中点数最少的顶点割称为最小点割
 注意
注意
- 若 是非平凡连通图,则 是 的割点当且仅当 是 的 1 顶点割
- 完全图没有顶点割,实际上也只有以完全图为生成子图的图没有顶点割
例: 均为 的顶点割,其中 为 1 点割, 为 2 点割, 为 3 点割, 没有顶点割
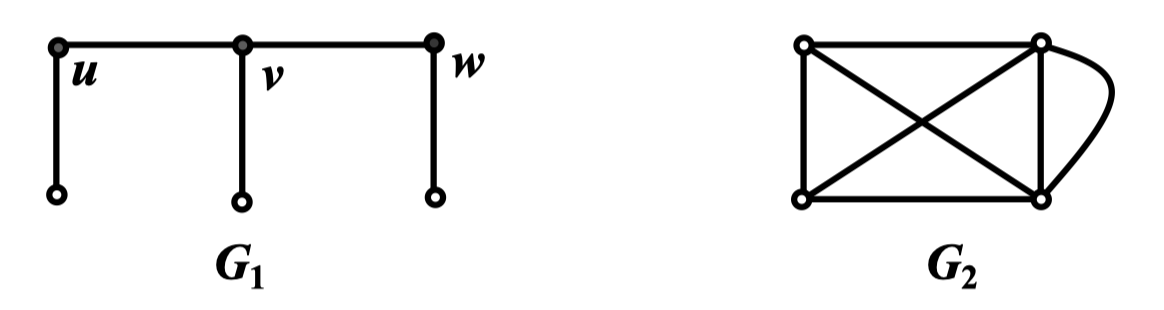
定义 49:对 阶非平凡连通图 ,若 存在顶点割,则称 的最小顶点割中的点数为 的连通度;否则称 为其连通度。 的连通度符号表示为 ,简称为 ;非连通图或平凡图的连通度定义为
 注:连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的点数”
注:连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的点数”
例:;,其中 为 圈,
例:求下列各图的连通度
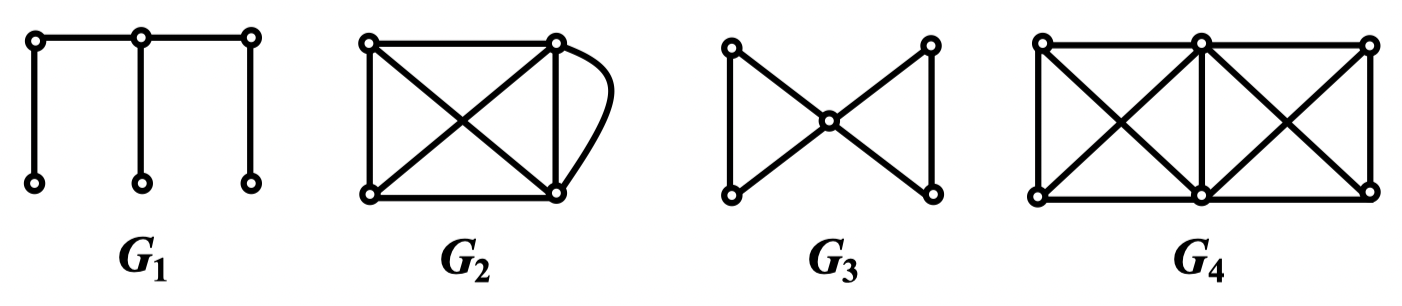
;;;
定义 50:若一个图的连通度至少为 ,则称该图是 连通的
 注意
注意
- 非平凡连通图均是 1 连通的 连通度为 1
- 图 是 2 连通的当且仅当 连通、无割点且至少含有 3 个点
- 连通、无割点,但连通度为 1
定义 51:设 为连通图,称使 不连通的 的边子集 为 的边割,含有 条边的边割称为 边割。边数最少的边割称为最小边割
 注:对连通图 ,由定义知, 是 的割边当且仅当 是 的 1 边割
注:对连通图 ,由定义知, 是 的割边当且仅当 是 的 1 边割
定义 52:设 是非平凡连通图,若 是 的最小边割,则称 为 的边连通度,记为 ,简记为 。非连通图或平凡图的边连通度定义为 0
 注:边连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的边数”
注:边连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的边数”
例:;,其中 为 圈,
例:求下列各图的边连通度
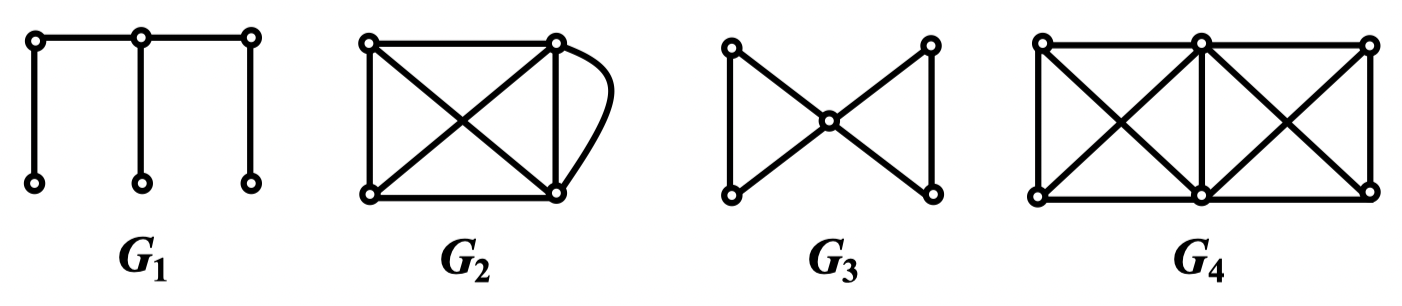
;;;
定义 53:若一个图的边连通度至少为 ,则称该图是 边连通的
 注意
注意
- 非平凡连通图均是 1 边连通的 边连通度为 1
- 图 是 2 边连通的当且仅当 连通、无割点且至少含有 2 个点 2 个点的圈
- 连通、无割点,但边连通度为 1
连通度的性质
定理 34:对任意的图 ,有
证明:若 为平凡图或不连通,则 ,显然结论成立。下设 为非平凡连通图
对任意的 ,由于全体与 相关联的边构成的集合是 的一个边割集,从而推知
下面对 用归纳法证明
当 时,
设对所有满足 的图 , 成立
假设 为边连通度等于 的任意一个图
设 是 的一个 边割,取
令 ,则 。由归纳假设知,
情况1⃣️: 含有完全图作为生成子图,则 也如此。此时
情况2⃣️: 的任意生成子图均不为完全图
设 是 的一个 顶点割,于是
若 不连通,则
若 连通,因 不连通,故 是 的割边
此时,若 恰含两个点,则
于是
若 至少含 3 个点,则 包含割点 ,于是 是 的顶点割,从而
所以总有
例:满足 的图
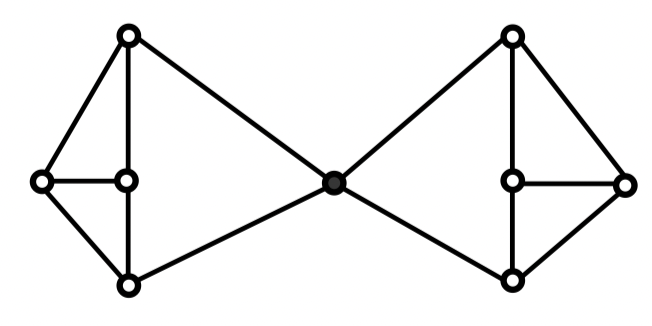
定理 35:设 是具有 条边的 阶连通图,则
证明:由握手定理
得:
例: 阶 连通图至少 条边
解释: 连通
故
引理:设 是 阶简单图,若 ,则 必连通
证明:若 不连通,则 至少有两个连通分支,从而必有一个分支 满足
因 是简单图,从而
于是
这与已知矛盾,所以 必连通
定理 36:设 是 阶简单图,对于正整数 ,若 ,则 是 连通的
证明:任意删去 中 个点,记所得之图为 ,则
因 是整数,故
而 是 的点数,由引理知 是连通的
所以 是 连通的
定理 37:设 是 阶简单图,若 ,则
证明:显然 是连通的
若 ,则
此时 中存在边割 ,满足 ,同时 是由两个不相交的子图 和 所构成
。。。。。。。。。。。。。。。。。
Menger 定理
定义 54:图中两条 路称为内部不相交或独立的,如果此两条路仅 和 是其公共点
定义 55:设 与 是图 中两个不同点,称一组点(边)分离 与 ,是指 中删去这组点(边)后不再有 路
例:点集 分离点 与 边集 分离点 与
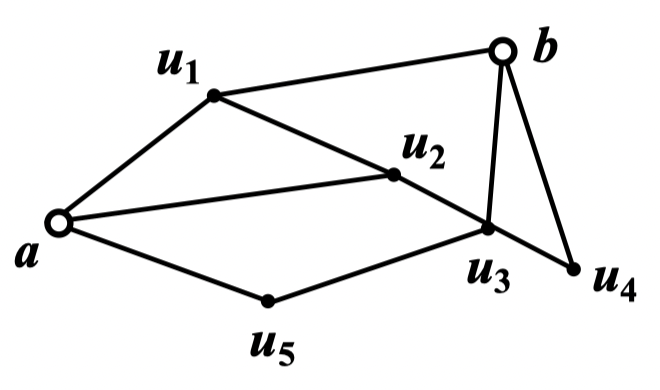
定理 38:
- 设 和 是图 中的两个不相邻点,则 中分离 和 的最少点数等于独立的 路的最大数目
- 设 和 是图 中的两个不同点,则 中分离 和 的最少边数等于边不重的 路的最大数目
例:在该图中,独立的 路的最大条数是 2,分离点 与 的最小点集是 ,包含 2 个顶点
在该图中,边不重的 路的最大条数是 3,分离点 与 的最小边集是 ,包含 3 条边
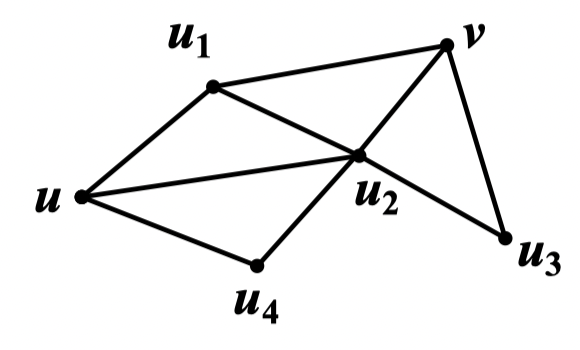
定理 39:
- 一个非平凡图 是 连通的当且仅当 的任意两个不同顶点间至少存在 条独立的路
- 一个非平凡图 是 边连通的当且仅当 的任意两个不同顶点间至少存在 条边不重的路
 注:「任意两个不相邻的顶点之间存在 条独立的路」 「任意两个相邻的顶点之间也存在 条独立的路」
注:「任意两个不相邻的顶点之间存在 条独立的路」 「任意两个相邻的顶点之间也存在 条独立的路」
例:设 是 连通图, 是由 中任意 个顶点构成的集合,若图 是由 通过添加一个新点 以及连接 到 中所有顶点得到的新图,求证: 是 连通的
证明:首先,分离属于 的两个不相邻顶点至少需要 个点
其次,分离 与 的不属于 的顶点至少需要 个点
因此,分离 中任意两个不相邻的顶点至少需要 个点,从而, 中任意两个不相邻的顶点间至少存在 条独立的路
所以, 中任意两个不同顶点间至少存在 条独立的路,因此 是 连通的
推论:设 是阶树至少为 3 的图,则以下三个命题等价
- 是 2 连通的无环图
- 无环且任意两点都位于同一个圈上
- 无孤立点且任意两条边都在同一个圈上
证明:
是 2 连通的无环图 无环且任意两点都位于同一个圈上
因为 是 2 连通的,则 的任意两个顶点间存在两条独立的路 和 ,显然 与 构成包含这两个顶点的一个圈
无环且任意两点都位于同一个圈上 无孤立点且任意两条边都在同一个圈上
中显然没有孤立点
设 与 是 的任意两条边,在 与 上分别添加两点 与 得图 ,不难证明 是 2 连通图
因此, 的任意两个顶点在同一个圈上,即 与 在 的同一个圈上,从而 与 在 的一个圈上
无孤立点且任意两条边都在同一个圈上 是 2 连通的无环图
显然无环,因为环和任意一条边不在同一个圈上。
设 与 是图 的任意两个不相邻顶点,由于 无孤立点,所以可设 分别与 相关联
因为 在同一个圈上,所以 与 在同一个圈上,因此分离 与 至少要删去两个点,即 是 2 连通的
应用
问题:如何构造出在给定可靠性的条件下使成本尽量低的系统?
图论模型:对一个赋权图 ,试确定 的一个具有最小权的 连通生成子图
 注意
注意
- 对于 ,此问题即为求最小生成树的问题
- 对于 ,这是一个还未解决的困难问题
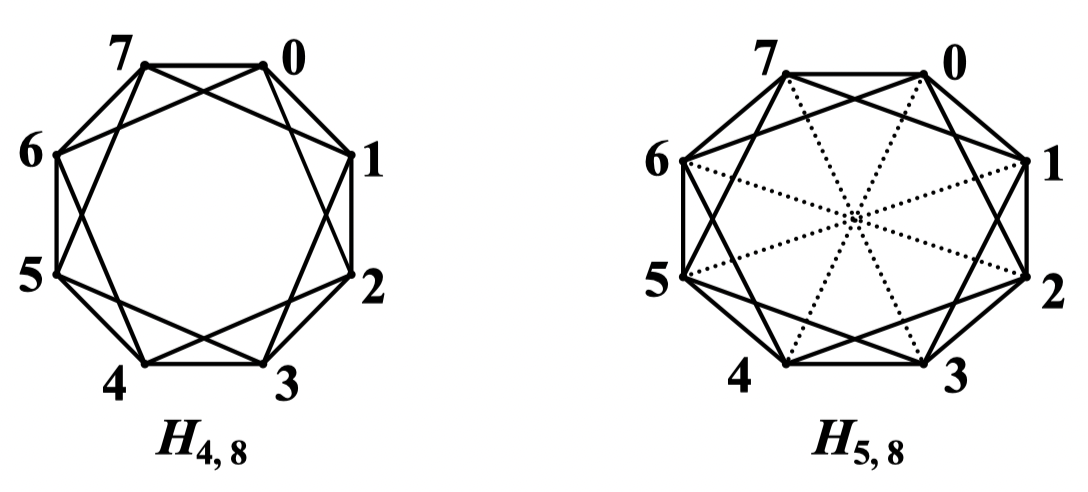
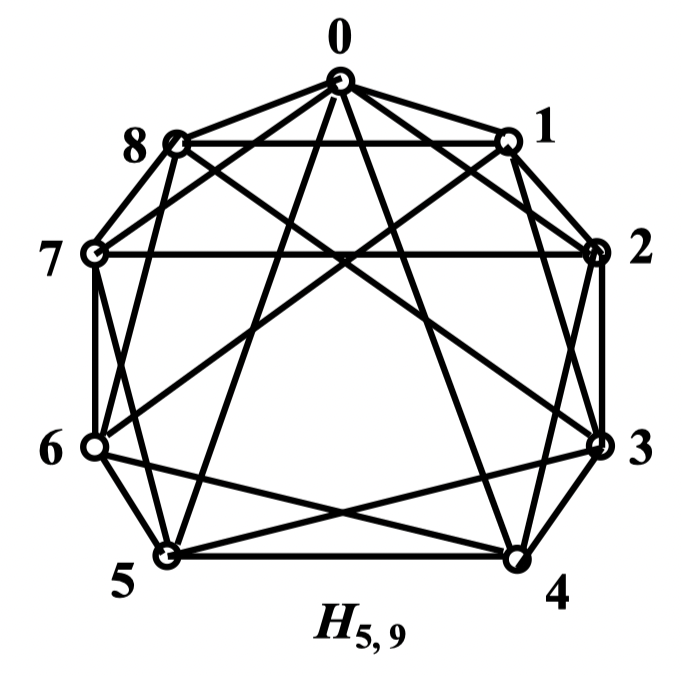
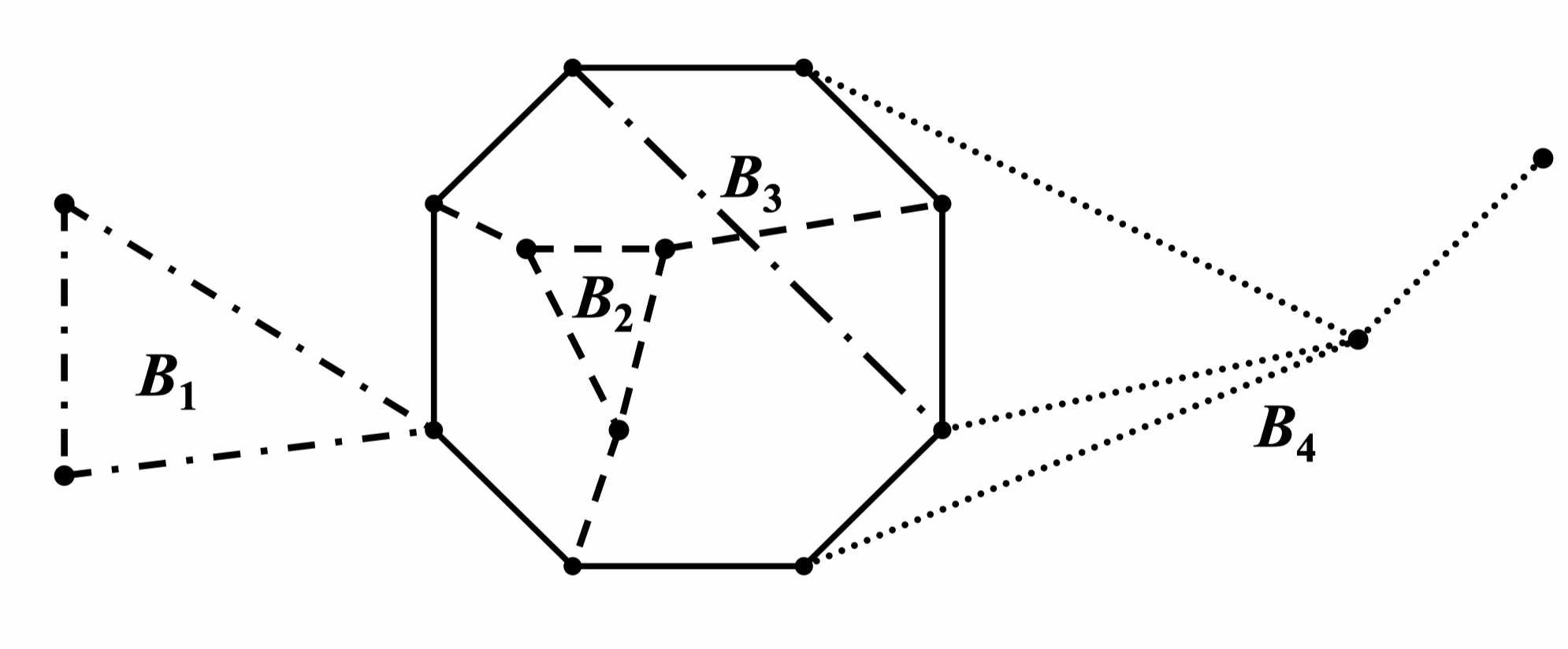
当 是完全图,各边的权均为 1 的特殊情况,问题是有解的。此时即求边数最少的具有 个顶点的 连通图 -> click
的构造:设
- 情况一: 为偶,设 。此时 与 连线; 与 连线;; 与 连线。如下图中的 所示
- 情况二:, 为偶,先作 ,再在 与 间添加边 。如下图中的 所示
- 情况三:, 为奇,先作 ,再在 与 , 以及 和 间添加边。如下图中的 所示
图的宽距离和宽直径
问题背景:
分析评价互联网络的性能指标有多个指标,其中包括传输延迟
传输延迟,又称时间延迟,是指信息从信息源传到目的地所需要的时间
如果度量网络的传输延迟??
- 信息从信息源到目的地需要经过若干中间站存储和转发
- 因此,信息传输延迟可以用图的顶点间距离来度量。每条边的长度可以定义为 1
- 网络的最大通信延迟可以通过图的直径来度量
宽直径:
定义 56:设 与 是图 中两个不同点, 表示 中 条独立的 路构成的路族,称之为 容器,简称容器; 称为该容器的宽度。容器 中最长路的路长定义为该容器的长度,记为
例:在该图中, 的一个宽度为 3 的 容器为:;该容器的长度为:
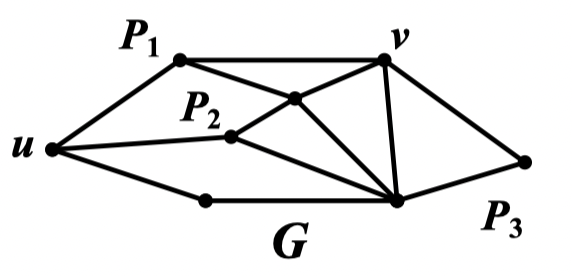
定义 57:设 ,定义 与 间所有宽度为 的容器的长度的最小值为 与 的 宽距离,记为 。即:
例:在该图中, 与 的 3 宽距离为:

定义 58:设 是 连通的, 的所有点对间的 宽距离的最大值,称为 的 宽直径,记为 。即:
 注意
注意
- 1 宽距离就是普通距离,1 宽直径就是普通直径
- 若图 是 连通的, 中任意两点见均存在 条内部不相交的路,所以 连通图的 宽直径, 宽直径,,1 宽直径均存在
例:求 点圈 和 阶完全图 的宽直径,其中
解:
- 显然
因为 中任意点对间只有一个唯一的宽度为 2 的容器,点对间的 2 宽距离就是该点对的唯一容器的长度。当 与 相邻时,容器的长度最长为 ,所以,宽度直径得:
- 显然
对于任意的 ,任意点对间的 宽距离为 2
所以有
定理 40:对于任意连通图 ,若图 的宽直径存在,则
定理 41:设 是 阶 连通图 ,则 ,而且上界和下界都能达到
第四章 Euler 图 & Hamilton 图
欧拉图
定义 59:经过 的每条边的(闭)迹被称为 (闭)迹,存在 闭迹的图称为 图,简称 图。 闭迹又称为 回路
 注意
注意
- 闭迹的起点和终点必须相同
- 若能遍历完所有的边但是没法回到起始点,称为非欧拉图但是有 迹
例: 是欧拉图, 不是欧拉图,但又欧拉迹, 不是欧拉图,也无欧拉迹
定理 42:假定 是一个连通图,则下列命题等价:
- 是欧拉图
- 的每个点的度数是偶数
- 的边集能划分为边不重的圈的并
证明:
是欧拉图 的每个点的度数是偶数
令 是 中的一条 闭迹
中任何一个给定的点在 中出现一次恰好关联两条边,因为 的每条边在 中仅出现一次,所以该点的度应为该点在 中出现的次数的两倍,所以是一个偶数
的每个点的度数是偶数 的边集能划分为边不重的圈的并
对 的边数归纳证明。
当 的边数为 1 时,此时 只能是自环,结论显然成立
假设 的边数大于 1,从任意一点出发,寻找一条通道直到某一个顶点再次遇到,假设为
则 到 的通路构成一个圈
从 中移去得到的圈,则得到的每个连通分支是一个满足条件,边数较少的图
由归纳假设知,结论显然成立
的边集能划分为边不重的圈的并 是欧拉图
令 是这个划分的一个圈,若 仅由这个圈组成,则 显然是欧拉图
否则,由另外一个圈 ,且 与 有一个公共点
从 开始并且由 与 相连组成的通道是含有这两个圈中各条边的一条闭迹
继续这个过程,我们可以构成一条含有 的所有边的闭迹,从而 是欧拉图
推论:连通图 有 迹当且仅当 最多有两个奇点( 仅是有 迹,而非 图)
仅是有 迹,而非 图)
证明:显然, 有 闭迹当且仅当 有零个奇点
若 有 非闭迹 ,并设点 和 分别是 的起点和终点
记在 中添加一条连接 和 的边 后所得到的图为
显然, 是一条 闭迹,则由已证结论知, 有零个奇点,从而 ,即 仅有两个奇点
反之,设 是恰有两个奇点 和 的连通图
在 和 间添加新边 得图 ,则 没有奇点
由已证结论, 有 闭迹,从而 有 迹
综上,结论成立
一笔画问题:画一个图形,在笔不离纸,每条边只画一次而不允许重复的情况下,画完该图
 注意
注意
- 一笔画问题本质就是一个图是否存在 迹 的问题
- 如果图 为欧拉图,则能够一笔画完该图,并且又回到出发点
- 如果图 只存在非封闭的欧拉迹,则能够一笔画完该图,但回不到出发点
例:在平台内,右图是否可以在三笔之内画成?
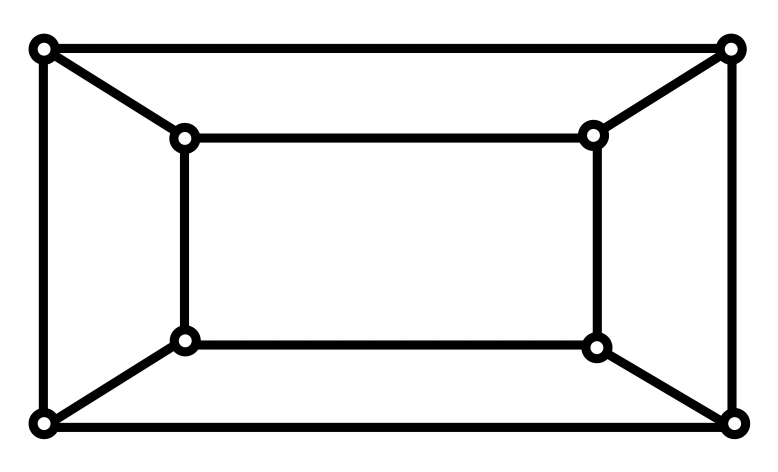
解:假设可以三笔画成,不妨用下图表示:
也就是说,在原图上添加三条边,可使其变成欧拉图
但原图有 8 个度数为奇数的顶点,添加三条边最多可以使 6 个顶点的度数变为偶数
因此,原图不能三笔画成
例:证明:若 有 个奇度顶点,则存在 条边不重的迹 ,使得:
证明:不失一般性,只就 是连通图进行证明
令 是 的所有奇度点
在 与 间连新边 得图 ,则 是欧拉图
因此,图 存在欧拉回路
在 中删去 ,得 条边不重的迹 :
思考题:
- 当 满足什么条件时,完全图 是欧拉图? 为奇数
- 当 满足什么条件时,完全图 方体 是欧拉图? 为偶数
- 若完全二部图 为欧拉图, 和 需满足什么条件? 均为偶数
思考题:假设图 恰好有两个连通分支,并且每个连通分支都是欧拉图,若要将 变为欧拉图,最少需要添加几条边? 最少需要添加 2 条边
思考题:欧拉图是否存在割边? 不存在
例:能否将一副多米诺骨牌排成一行,使得对于任意相邻的两块牌,他们的接触面具有相同的点数?

解:存在满足条件的排列方式
每块骨牌可以用唯一的一对数字 来表示,其中 ;比如, 表示骨牌
以数字 为顶点,先构造完全图 ,然后在每个顶点处再添加一个自环,所得图用 来表示
图 的每条边对应一块骨牌,比如顶点 处的自环表示骨牌
问题转化为判断图 是否为欧拉图
图 的每个顶点的度数为 8。因此, 是欧拉图
Fleury 算法
算法思想: 从任一点出发按以下方法来描画一条边不重复的迹,使在每一步中未描画的子图的割边仅当没有别的边可选择时才被描画
Fleury 算法
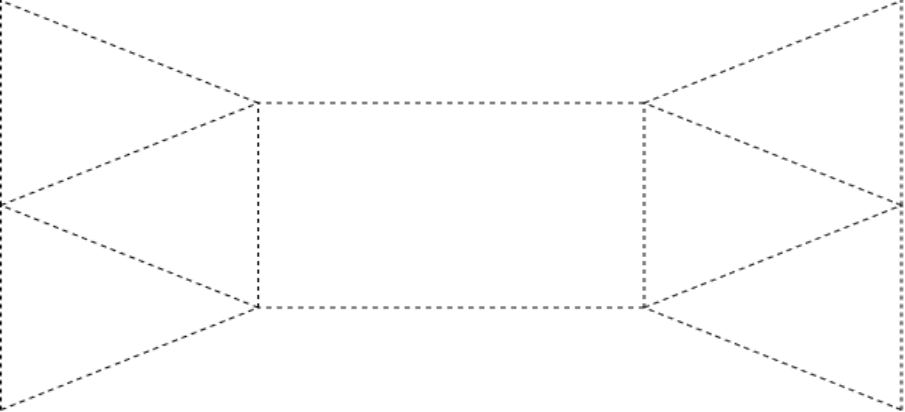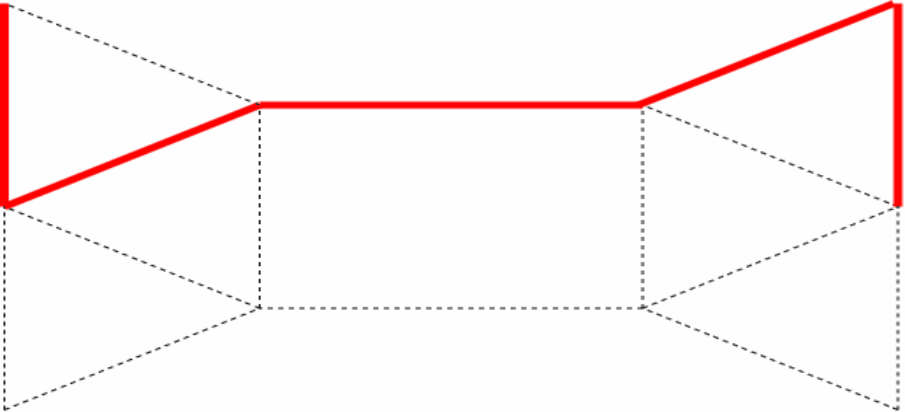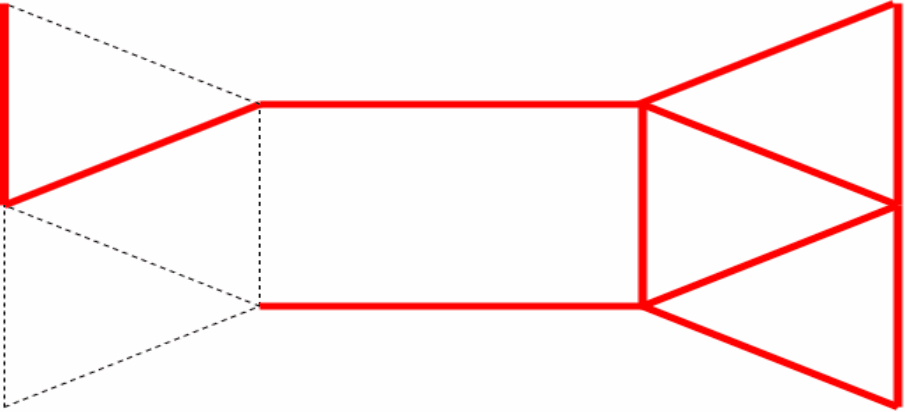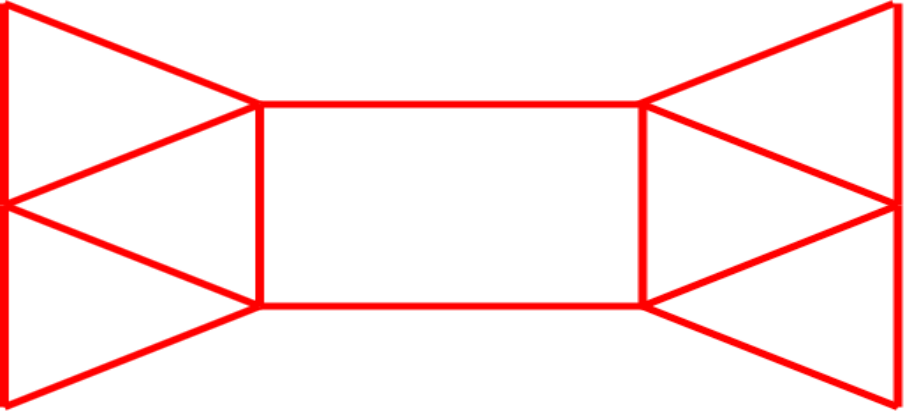
例:某博物馆的一层布置如下图,其中边代表走廊,结点 是入口,结点 是礼品店,通过 我们可以离开博物馆。请找出从博物馆 进入,经过每个走廊恰好一次,最后从 处离开的路线
解:图中只有两个奇度顶点 和 ,因此存在起点为 ,终点为 的欧拉迹
为了在 中求出一条起点为 ,终点为 的欧拉迹,在 和 间添加一条平行边 ,如图所示
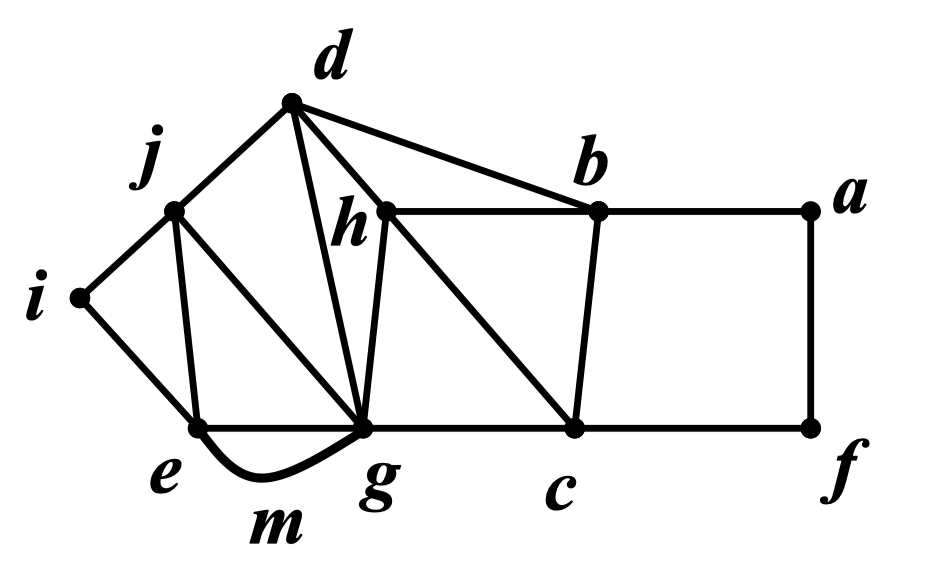
用 Fleury 算法求出欧拉回路为:
所以要求的路线为
中国邮递员问题
问题描述:邮递员从邮局出发,递送邮件,然后返回邮局,要求辖区每条街至少走一遍且走过的总路程最短,应如何选择路线?
图论模型:在一个连通具有非负权的赋权图 中找到一条包含每条边(允许重复)且边权之和最小的闭途径,称之为最优环游
 注意
注意
- 若图 是一个欧拉图,则找出 的欧拉回路即可
- 对一般图,其解法为:添加重复边以使 称为欧拉图 ,并使添加的重复边的边权之和为最小,再求 的欧拉回路
定理 43:假定 是在图 中添加一些重复边得到的欧拉图,则 具有最小权值的充要条件是:
- 的每一条边最多被添加一次
- 对于 的每个圈来说,该圈新添加的边的总权值不超过该圈总权值的一半
证明:必要性
若 中某条边在 中被添加的次数超过 1,则去掉其中两条重复的边,我们将得到一个总权值更小,且以 为生成子图的欧拉图
上述与 “ 总权值最小” 相矛盾,因此每条边最多被添加一次
假定在 中存在某个圈使得该圈新添加的边的总权值大于该圈权值的一半,不妨设为
那么在 中,将 上新添加的边全部去掉,然后将原圈未添加新边的边都添加一条重复边
这样的操作使得该圈所有点的度数不变或改变 2,相应的图仍然是欧拉图,但是权值更小,这与 “ 总权值最小” 相矛盾
充分性:我们将证明「满足条件的任何两个图都具有相同的总权值」
设 和 分别表示 与 中添加的边的集合
要比较 与 总权值,我们只需考虑集合 与集合 的权值
令:
考察由边集 导出的子图
断言 1: 的每个顶点的度数必然为偶数
对于 中任意点 ,如果 是奇数,那么 中与 中与 关联的边数均为奇数
如果 是偶数,则 与 中与 关联的边数均为偶数
其次,设 与 中与 关联的边数分别为 与 ,其中相同的边数为 ,那么, 中与 关联的边数为:
所以, 中与 关联的边数为偶数,说明 的每个顶点的度数必然为偶数
由于 的每个顶点的度数为偶数,所以它的每个分支是欧拉图。因此, 可以作圈分解
设
断言 2:对每个 ,均成立
事实上,因为:
又因为:
所以,对每个 ,成立
因此
由断言 2 可知, 和 具有相同的权值
非 图求最优环游的方法:
- 用每条边最多添一次的方法任意添一些重复边使图 成为一个欧拉多重图
- 考查 的圈,若存在圈 ,其中重复边的总权值大于该圈权值的一半,则在圈 上交换重复边和不重复边得到一个新的欧拉多重图。重复这个过程,直到得到一个图 ,使得图 中每个圈上重复边的总权值不大于该圈权值的一半
- 用 Fleury 算法求 的 回路
例:图 如图 (a) 所示(各边权值为 1),它有 10 个奇度点。任意添一些边得到一个欧拉多重图 (b)
(b) 中有色圈中重复边的数目为 5,大于圈长 8 的一半,在这个圈上交换重复边和不重复边,得到 (c)
(c) 中每一个圈中重复边的数目均不大于圈长的一半。从而,由 (c) 中每条欧拉回路对应原图一条闭通道,它含有所有的边且具有最短的长度
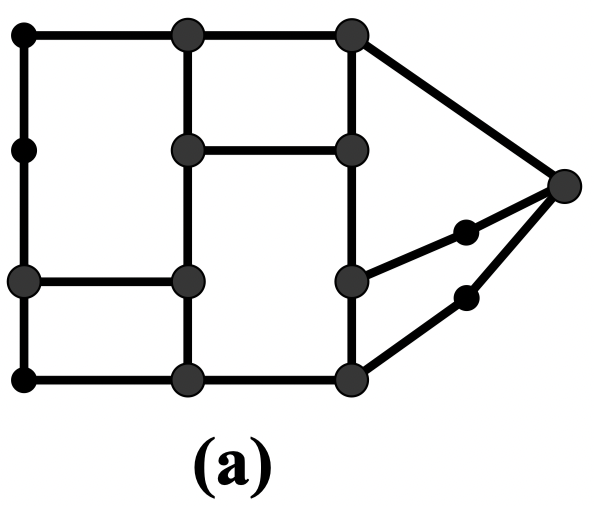
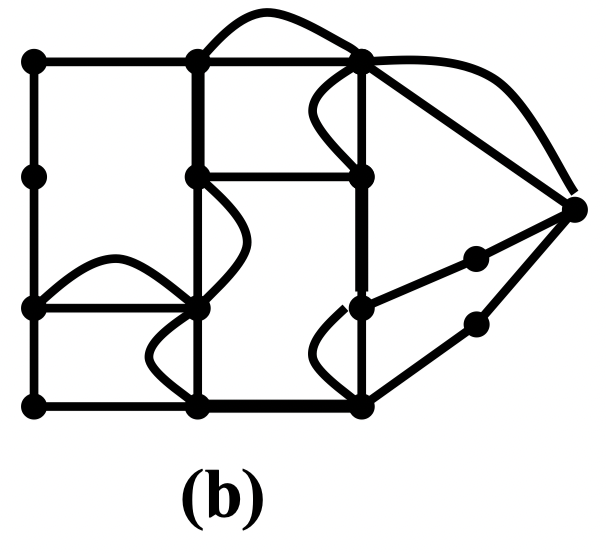
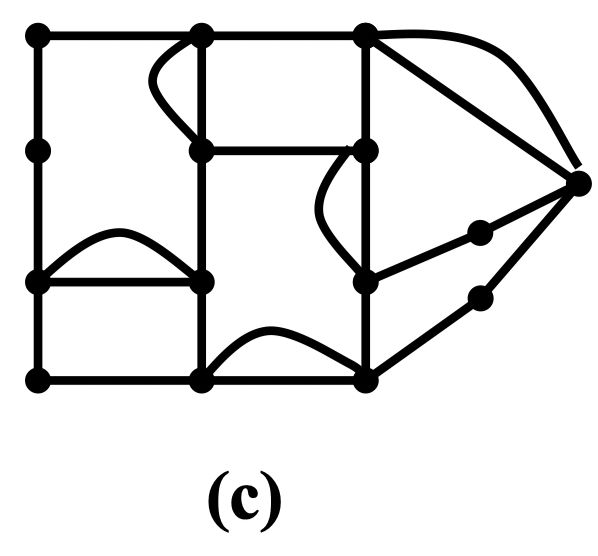
例:求图 的一个最优欧拉环游
解:
例:设图 是具有 个奇度顶点,则在 中最少添加 条边才能使 具有欧拉回路
例:如果一个赋权图 中只有两个奇度顶点 与 ,设计一个求其最优欧拉环游的算法
解:
- 在 与 间求出一条最短路 ;(最短路算法)
- 在最短路 上,给每条边添加一条平行边得到 的欧拉多重图
- 在欧拉多重图 中用 Fleury 算法求出一条欧拉回路
证明算法的合理性
设 与 是 的两个奇度点, 是 的任意一个欧拉多重图
考虑 ,显然它只有两个奇度顶点 与 ,当然它们必须在 的同一个分支中,因此,存在 路
所以
例:求出下图的一条最优欧拉环游
最优欧拉环游:
权值:37
哈密尔顿图
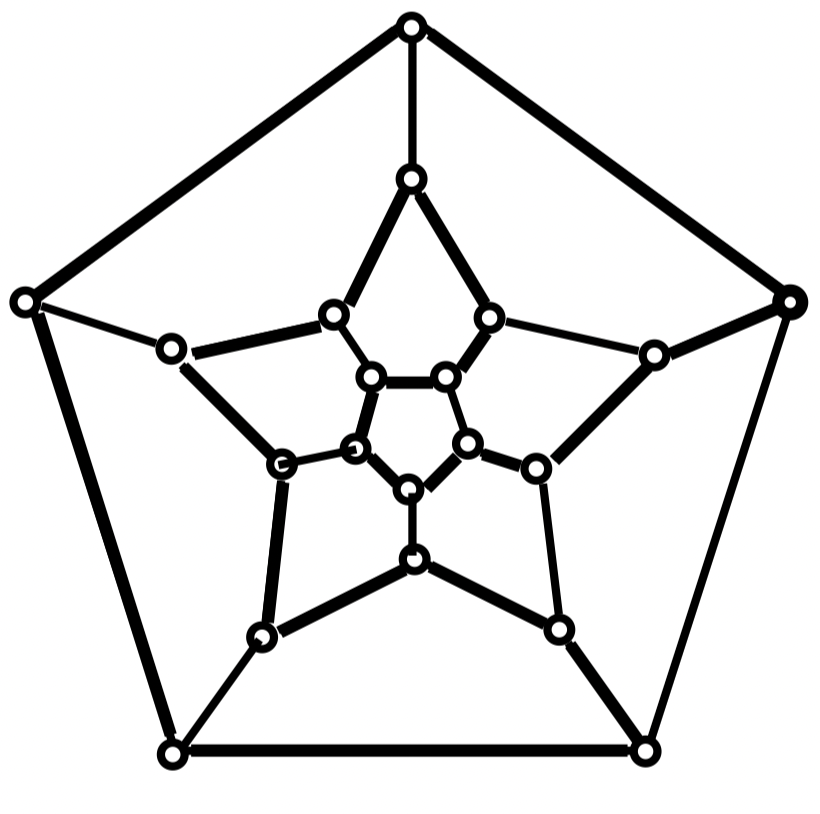
1857 年,哈密尔顿发明了一个游戏 (Icosian Game)。它是由一个木制的正十二面体构成,在它的每个棱角处标有当时很有名的城市。游戏目的是“环球旅行”。为了容易记住被旅游过的城市,在每个棱角上放上一个钉子,再用一根线绕在那些旅游过的城市上 (钉子),由此可以获得旅程的直观表示
该游戏促使人们思考点线连接的图的结构特征。这就是图论历史上著名的哈密尔顿问题
定义 60:经过图中每个点的路称为 Hamilton 路,简称 路
定义 61:经过图中每个点的圈称为 Hamilton 圈,简称 圈
定义 62:存在 Hamilton 圈的图称为 Hamilton 图,简称 图
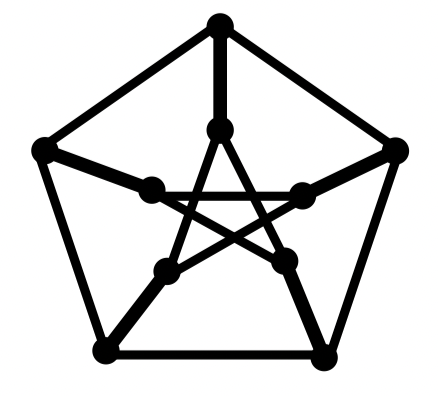
例:正十二面体图是 Hamilton 图
思考
- 当 时,完全图 是否为哈密尔顿图? 是
- 当 时, 方体 是否为哈密尔顿图? 是
- 若完全二部图 为哈密尔顿图, 和 需满足什么条件?
思考:是否存在一个具有奇数个顶点的连通图,它既是二部图,也是哈密尔顿图? 不存在,否则二部图中出现了奇圈 定理 9
思考:若二部图 是哈密尔顿图,则它的二部划分 满足什么条件?
定理 44:若 是 图,则对于 的每个非空真子集 ,均有
证明:设 是 的 圈
对 的任意非空子集 ,容易知道
所以
 注:上述定理只是必要条件,而非充分条件
注:上述定理只是必要条件,而非充分条件
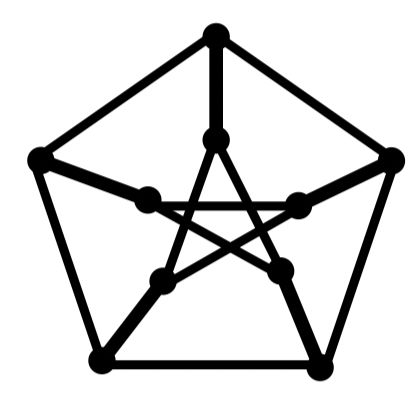
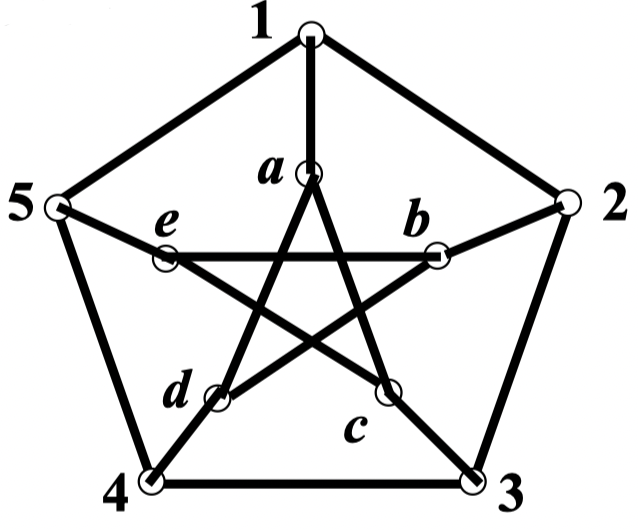
例:证明:彼得森图不是 图,但满足定理中的条件
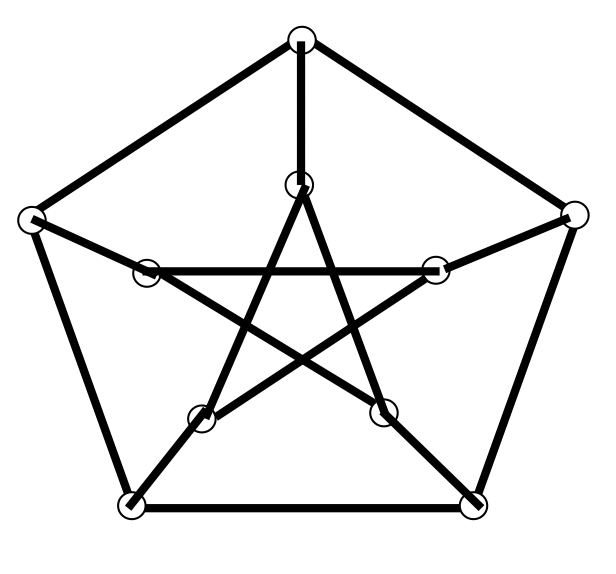
证明:可以直接验证彼得森图满足定理中的条件
接下来证明彼得森图不是 图
假定彼得森图是 图,对其顶点进行标号,如下图所示
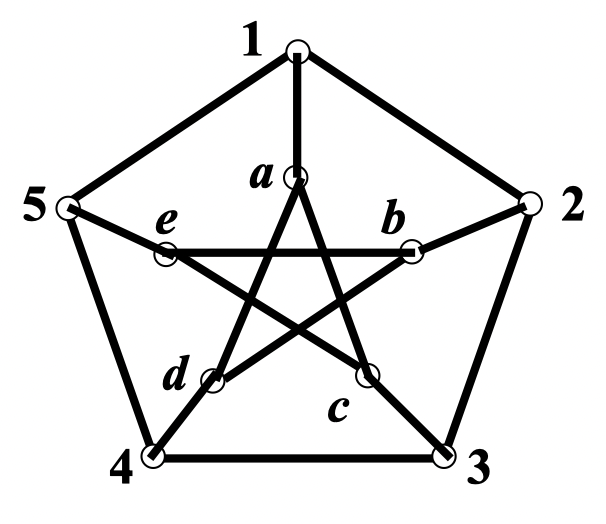
哈密尔顿圈 必然从外面的圈 123451 沿着一条辐轴边 进入里面的圈 ,然后再沿着另一条辐轴边回到外面的圈 123451
因此, 必然经过 2 条或者 4 条辐轴边
情况 1:
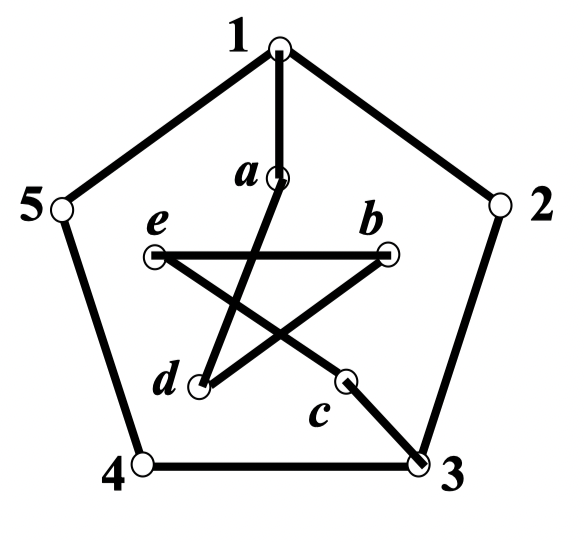
经过 2 条辐轴边
不妨假设经过了辐轴边
对于边 和 ,有且仅有 1 条在圈 上,不妨假设为
因为边 不在圈 上,则辐轴边 一定在圈 上
从而,辐轴边 一定不在圈 上
此时,顶点 2 和顶点 4 的度数均为 2。因此,边 23 和 43 一定在圈 上
我们推出:顶点 3 关联的 3 条边都在圈 上,矛盾!
情况 2:

经过 4 条辐轴边
不妨假设未经过市轴边
因为边 15 和 都在圈 上,所以边 12 一定不在圈 上,从而边 23 一定在圈 上
显然,边 和 一定在圈 上
此时,边 23,,, 和 已经构成一个圈,矛盾
利用定理可以说明某些图不是哈密尔顿图
例:判断图 是否为哈密尔顿图?
解:取 ,则
因此, 不是哈密尔顿图
例:若连通图 不是 2- 连通的,则 不是哈密尔顿图
证明:因为连通图 不是 2- 连通的,则 存在割点
显然,
因此, 不是哈密尔顿图
哈密尔顿简单图中一定不存在割点
例:若图 包含哈密尔顿路,则对 的每个真子集 ,
证明:设 为图 的哈密尔顿路
显然,
定理 45 (Dirac 1952):对于 的简单图 ,如果 中有:,那么 是 图
证明:
定理 46 (Ore 1962):对于 的简单图 ,如果 中的任意两个不相邻顶点 与 ,有:,那么 是 图
例:设 是由 的一个顶点和另一个 的一个顶点重合得到的图,那么对于 的任意两个不相邻顶点 和 ,显然有 ,但 不是 Hamilton 图
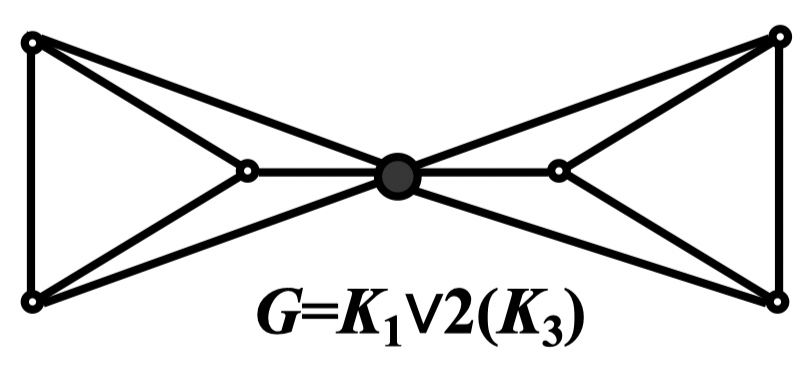
定义 63:在 阶简单图 中,若对 的任何一对点 和 都是相邻的,则称 是闭图
定理 47:若 和 是同一个点集 的两个闭图,则 是闭图
证明:因对任何 ,有 ,
故由 ,可得 ,
由 和 是闭图, 和 在 和 中都邻接,故 和 在 中也邻接,从而 是闭图
 注:闭图的并图并 () 不一定是闭图
注:闭图的并图并 () 不一定是闭图
例:尽管 与 是闭图,但其并不是闭图!!
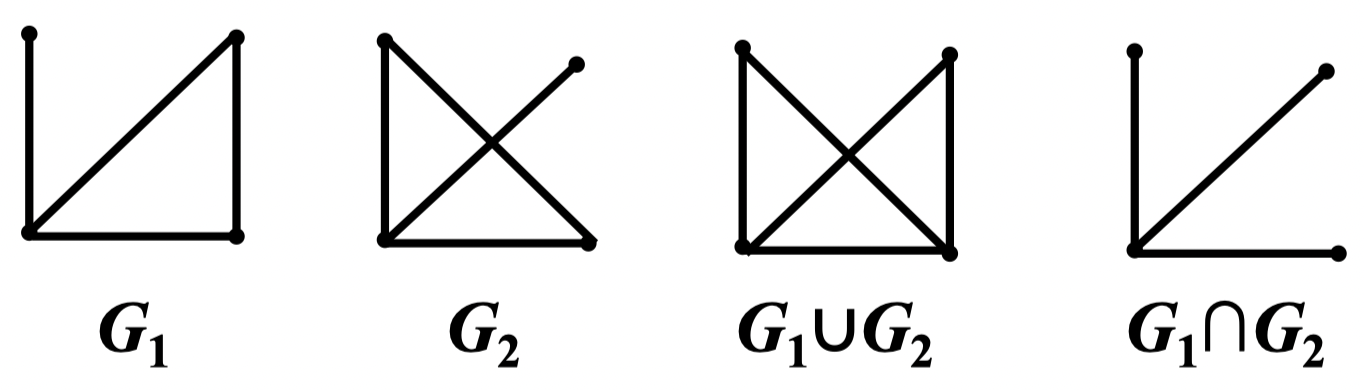
定义 64:若一个与 有相同点集的闭图 ,使 ,且对异于 的任何图 ,若有 ,则 不是闭图,则称 是 的闭包
 注: 的闭包是包含 的极小闭图
注: 的闭包是包含 的极小闭图
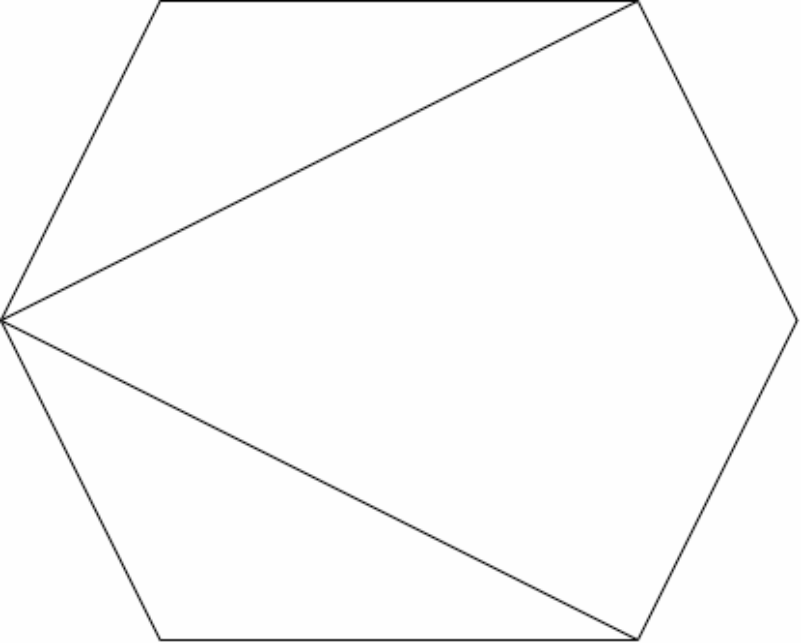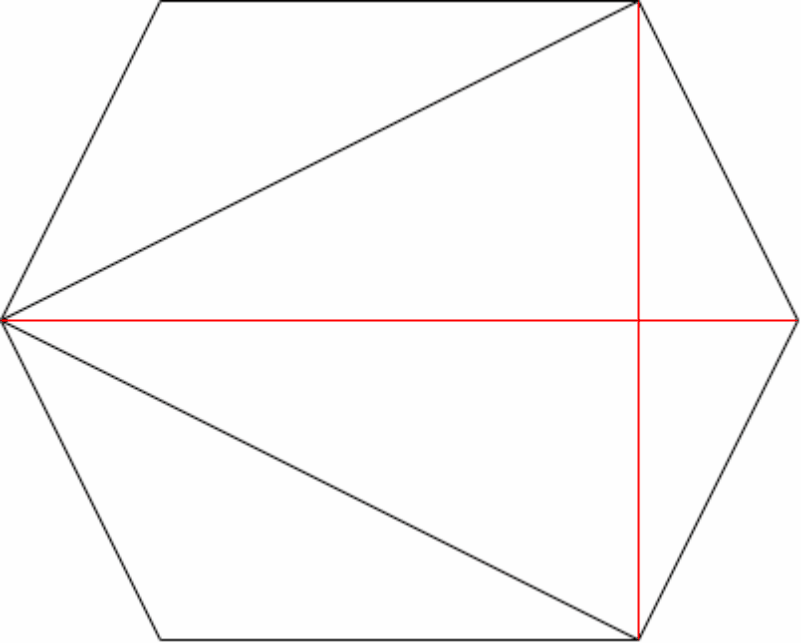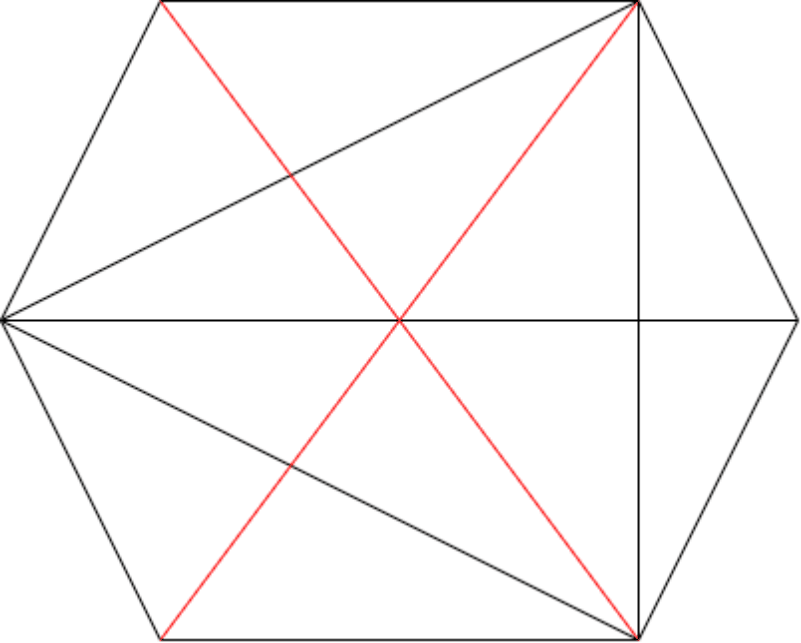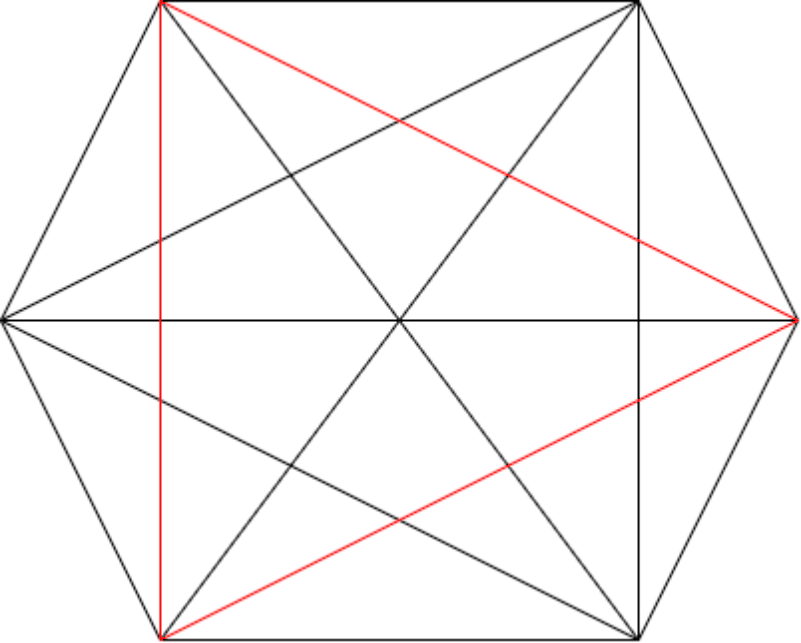
图的闭包的构造方法:将图中度数之和至少是图的顶点个数的非邻接顶点对递归地连接起来,直到不再有这样的顶点对存在为止
例:下图给出了 6 个顶点的图的闭包的构造过程
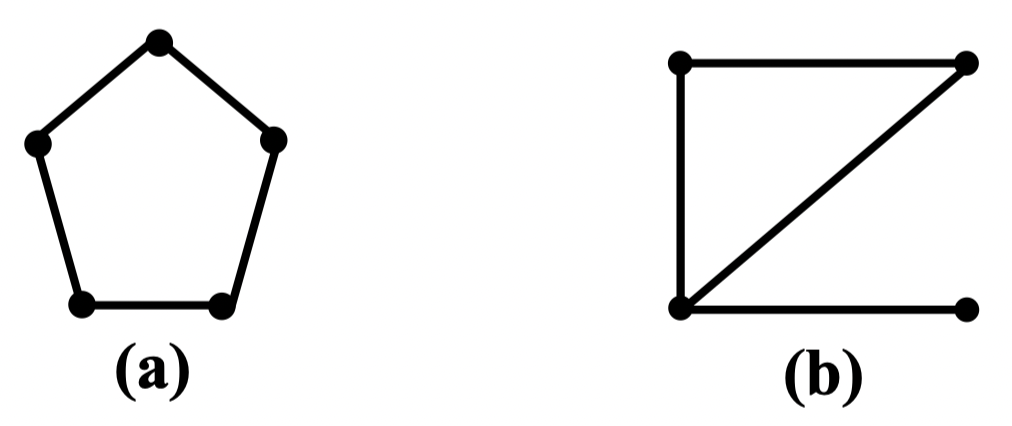
 注:一个图的闭包不一定是完全图。比如下图中 (a)、(b) 两个均不是完全图,但它们却是自己的闭包
注:一个图的闭包不一定是完全图。比如下图中 (a)、(b) 两个均不是完全图,但它们却是自己的闭包
定理 48:任意图 的闭包是唯一的
证明:设 和 是 的闭包,则显然由 ,
因此
又因为 是闭图 (前提: 和 是闭图;定理 47),且 ,
故由闭包的定义知 ?????
因此, 的闭包是唯一的
引理:设 是 阶简单图, 和 是 中不相邻的顶点,且满足 ,则 是 图的充要条件是 为 图
证明:
必要性:若 是 图,则显然 也是 图
充分性:设 是 图, 是一个 圈
如果圈 不含边 ,则由 知 中有一个 圈
如果圈 中含有 边,不妨设该圈为
令 ,则 ,
故有:
断言:一定存在 使得 与 相邻, 与 相邻
..........
定理 49 (Bondy):一个简单图 是 图当且仅当它的闭包是 图
证明:若 的闭包和 相同,结论显然成立
若 的闭包和 不同,设 是为构造 的闭包而依次添加的所有边
是 图当且仅当 是 图, 是 图当且仅当 是 图,,反复下去,可以得到定理结论
推论:设 是 的简单图,若 的闭包是完全图,则 是 图
推论:设 是 的简单图
- 若 中每个点的度 ,则 是 图
- 若 中任何两个不邻接的点 和 均有 ,则 是 图
定理 50 (度序列判定法):设简单图 的度序列是 ,这里, 并且 。若对任意的 ,或有 ,或有 ,则 是 图
证明:
断言: 的闭包必是 ,从而 是 图
..........
例:求证图 是 图
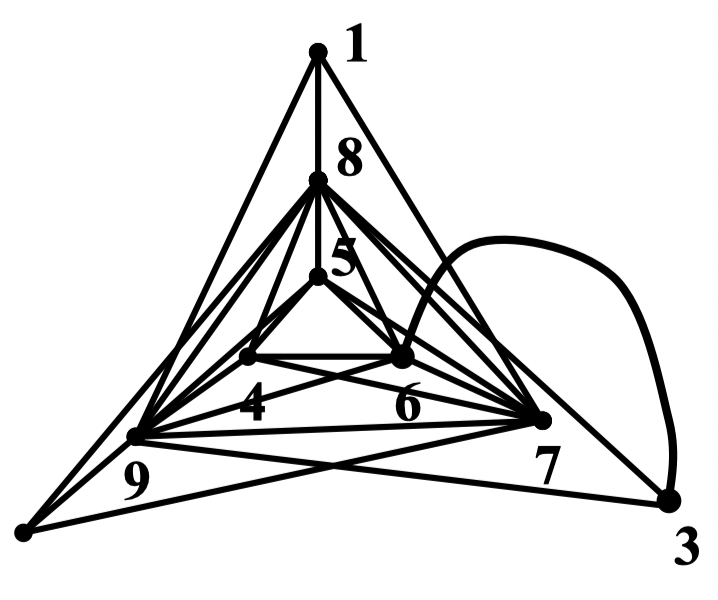
证明:在 中有 ,,,,
因 ,,,, 满足度序列判定定理的条件,因此是 图
例:设 是度序列为 的非平凡简单图,且满足 。证明:若不存在小于 的正整数 ,使得: 且 ,则 有 路
证明:在 之外上一个新点 ,把它和 的所有顶点连接得图
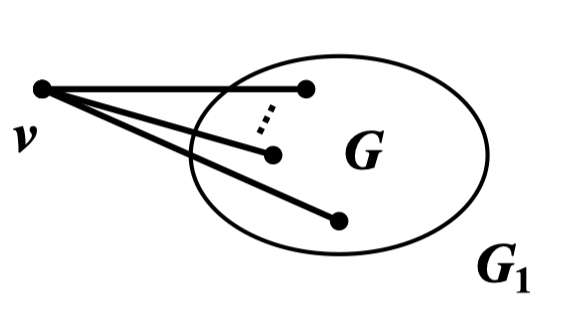
显然, 的度序列为:
由条件知:不存在小于 的正整数 ,使得 ,且
于是由度序列判定定理知: 是 图,得 有 路
例:设 是具有 个点的 正则图,其中 且 。证明:图 的补图是 图
证明:显然,图 的补图是 正则图,度序列为
因为 ,所以
对任意的 ,分两种情况讨论
- 若 ,则
- 若 ,则
综上,图 的补图满足度序列判定定理。因此,图 的补图是哈密尔顿图
应用
例:一只老鼠吃 立方体乳酪。其方法是借助于打洞通过所有的 27 个 的子立方体。如果它从一角上开始,然后依次走向未吃的立方体,问吃完时是否可以到达中心点
解:如果把每个子立方体模型为图的顶点,且两个顶点连线当且仅当两个子立方体有共同面。那么问题转化为问该图中是否存在一条由角点到中心点的 路
例:今有 七个人围圆桌开会,已知: 会讲英语, 会讲英语和汉语, 会讲英语、意大利语和俄语, 会讲日语和汉语, 会讲德语和意大利语, 会讲法语、日语和俄语, 会讲法语和德语。是否存在一种排座方法,使每个人能够和他身边的人交流?并说明理由
解:以每个人作为图的顶点,且两个顶点连线当且仅当两个人会讲同一种语言,得到图 如下
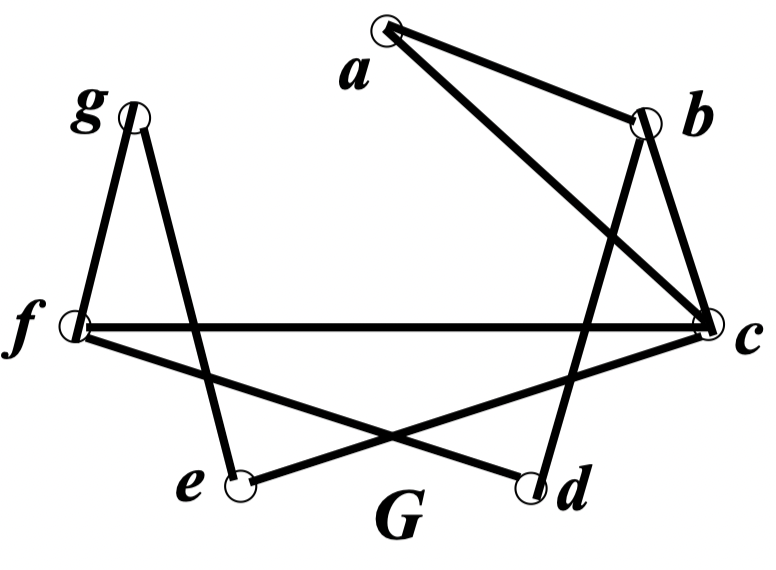
那么,问题转化为判断图 是否为哈密尔顿图
显然,是在 中可以找到一个 圈
因此,按照 的方式就座可以使每个人都可以和身边的人互相交流
度极大的非 Hamilton 图
定义 65:图 称为度极大非 图,若它的度不弱于其他非 图
定义 66:对于 , 图定义为:
例: 与 如图
引理:对于 的图 不是 图
证明:取 ,则 ,所以,由 图的性质知, 不是 图
定理 51 (Chvátal 1972):若 是 的非 简单图,则 度弱于某个 图
证明:设 是度序列为 的非 简单图,且
由度序列判定法:存在 ,使得 ,且
于是, 的度序列必弱于如下序列:
而上面序列正好是图 的度序列
 注意
注意
- 定理刻画了非 简单图的特征: 图族中每个图都是某个 阶非 简单图的极图
- 如果 阶简单图 度优于所有的 图族,则 一定是 图
- 定理的条件是必要条件而非充分条件
例: 阶圈 的度序列是 ,它度弱于 的度序列 ,但 是 图
例:判定图 是否为 图
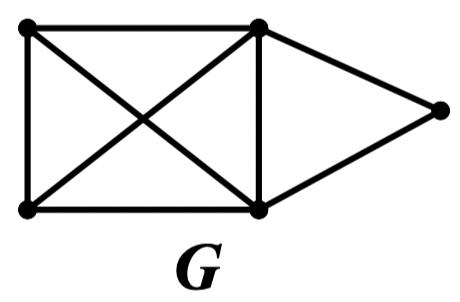
解: 的度序列是 ,优于 的度序列 和 的度序列 。所以可以判定 是 图
推论:设 是 阶简单图。若 且
则 是 图;并且,具有 个顶点, 条边的非 图只有 以及
证明:
 注:推论的条件是充分而非必要的。例如
注:推论的条件是充分而非必要的。例如
例:设 是 阶简单图。若 且
则 的闭包是完全图
证明:
旅行售货员问题
E 图和 H 图的联系
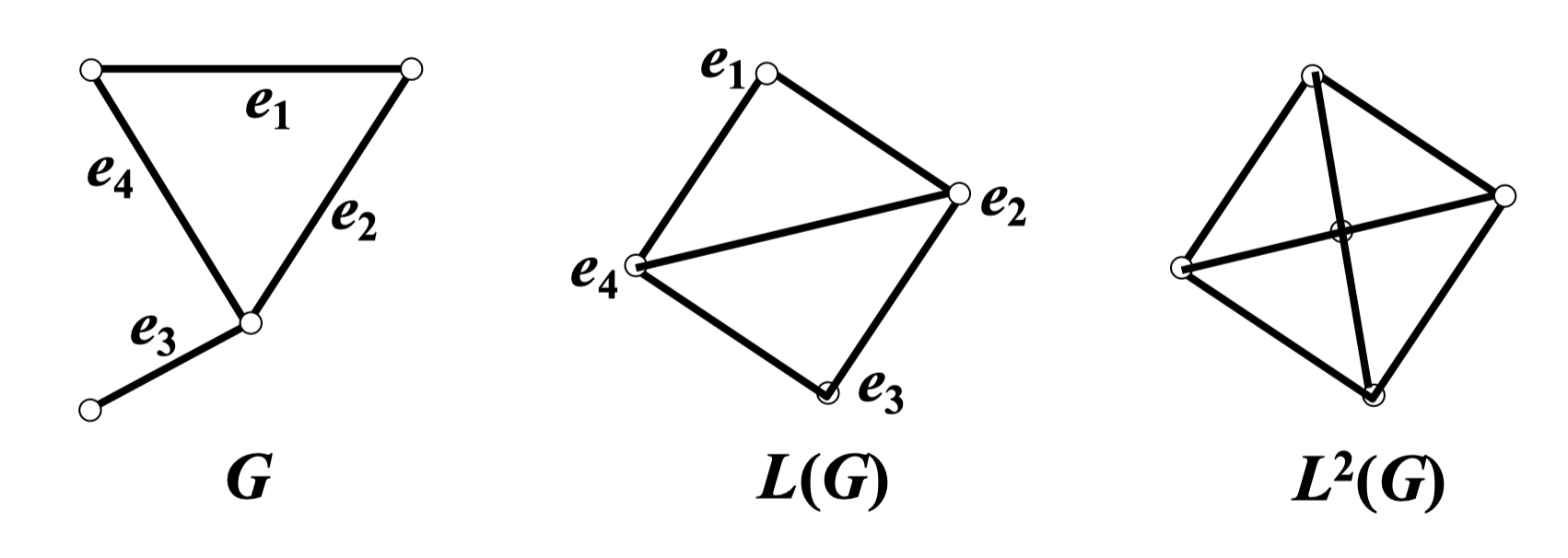
定义 67:图 的线图 定义为
- 当且仅当 与 中相邻
特别地, 的 次迭线图 定义为
例:
定理 52:
- 线图 顶点数等于 的边数
- 若 是 的边,则 作为 的顶点,度数为
定理 53:若 具有 个点, 条边,则线图 的边数为
证明:由定义知, 有 个顶点
对于 中任一顶点 ,关联于该顶点的 条边在 中产生的边数为
因此, 的边数为:
定理 54:一个图同构于它的线图当且仅当它是圈
定理 55:若图 和 有同构的线图,则除了一个是 而另一个是 外, 和 同构
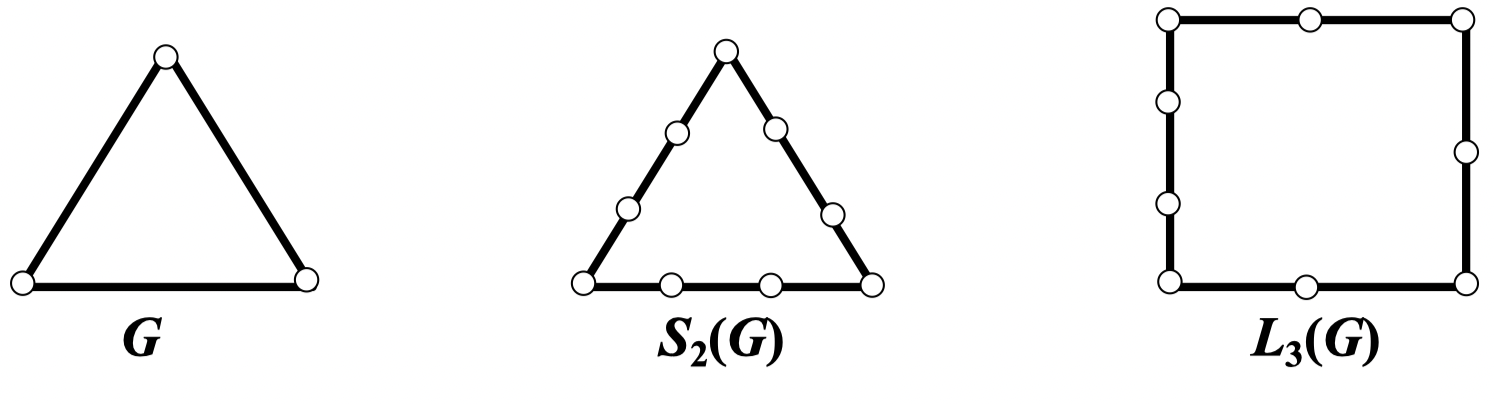
定义 68:称 是图 的 次细分图,是指将 的每条边中都插入 个 度顶点
例:

定义 69:
 注:一般地,
注:一般地,
定理 56:
- 若 是 图,则 既是 图又是 图
- 若 是 图,则 是 图
 注:该定理的逆命题不成立
注:该定理的逆命题不成立
定理 57:一个图 是 图的充要条件是 为 图
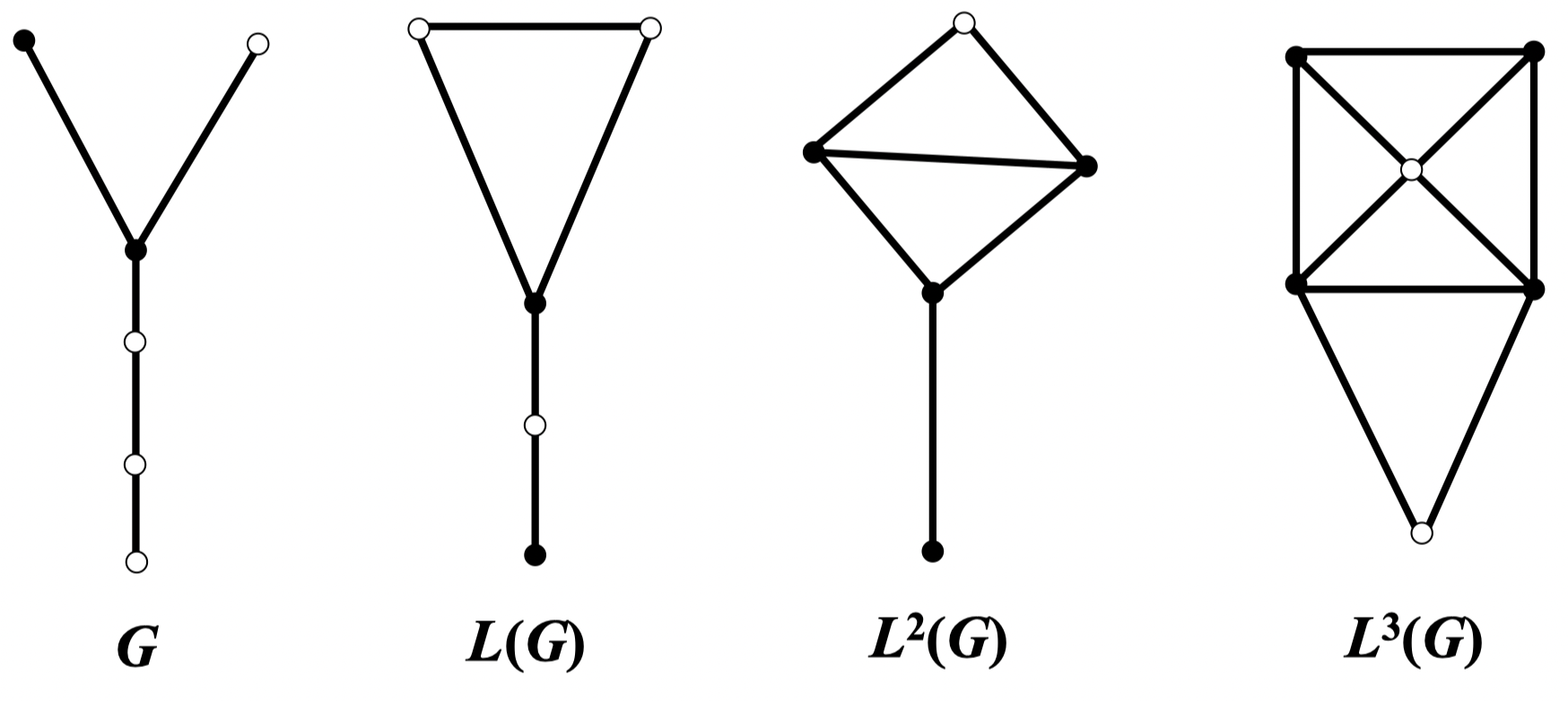
例:
定理 58:若 是具有 个点的非平凡连通图且不是一条路,则当 时,图 是 图
例:
第五章 匹配与因子分解
图的匹配
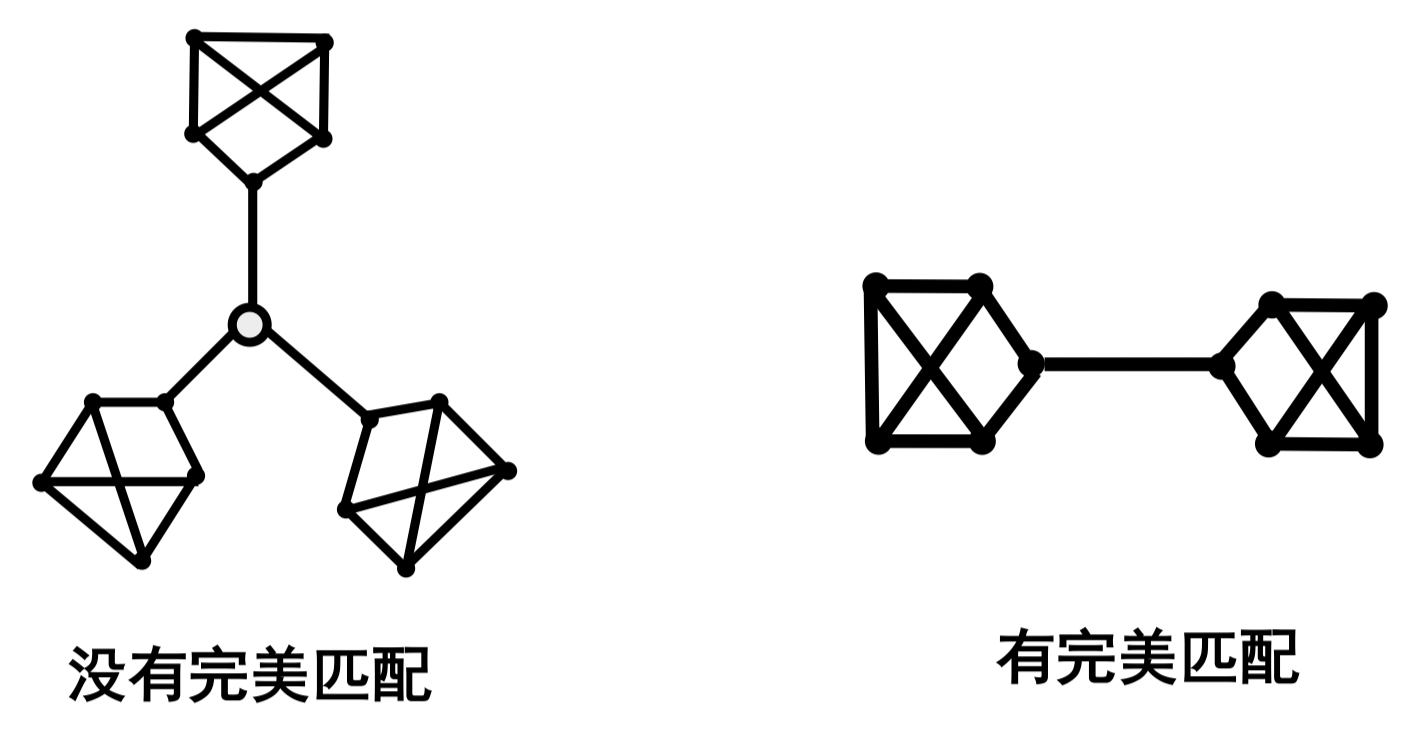
定义 70:设 是图 的边子集,若任意的 , 都不是环,且属于 的边互不相邻,则称 为 的一个匹配。设 为 的一个匹配,对 ,若 是 中某边的一个端点,则称 为 饱和点,否则称为 非饱和点
定义 71:如果 的每个顶点均为 饱和点,则称 为 的完美匹配
定义 72:如果 是图 的包含边数最多的匹配,则称 为 的最大匹配
 注意
注意
- 完美匹配必是最大匹配,而最大匹配不一定是完美匹配
- 最大匹配必存在,但完美匹配不一定存在
- 图 存在完美匹配的一个必要条件是 的点数必然是偶数
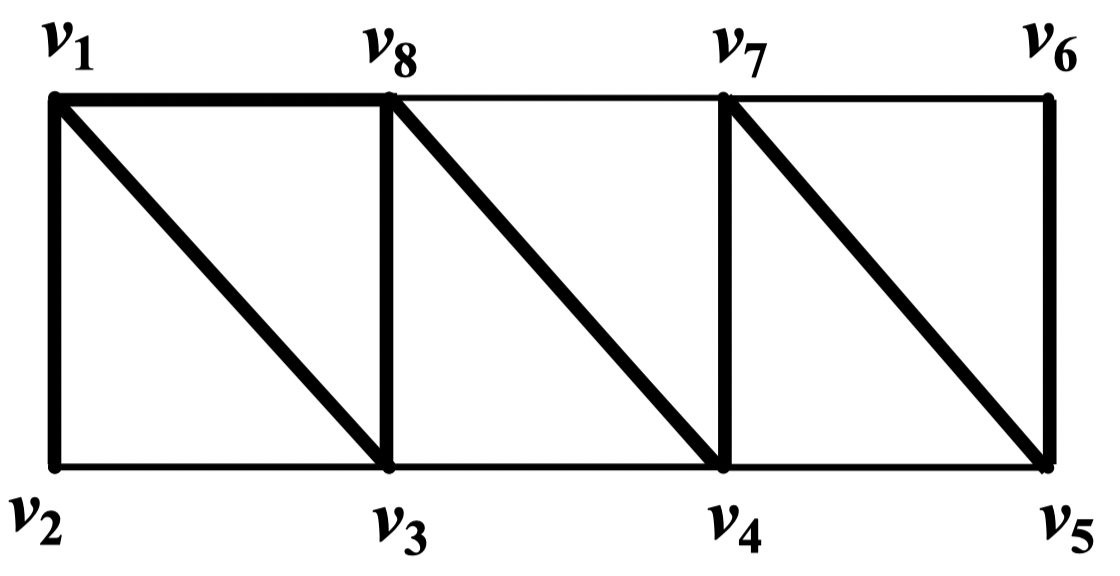
例:设图 如下图所示。 的匹配有:
对 ,点 是饱和点,点 是非饱和点
对 ,点 与 均是饱和点
和 既不是完美匹配,也不是最大匹配;而 是最大匹配,也是完美匹配
定义 73:设 为图 的一个匹配, 的 交错路是指 中由 中的边与非 中的边交替组成的路。 可扩路是指其起点与终点均为 非饱和点的 交错路
例:设匹配 ,则路 与 都是 交错路。其中 是 可扩路
Berge 定理
定理 59 (Berge 1957):图 的匹配 是最大匹配当且仅当 中不含 可扩路
证明:设 是 的最大匹配,并假设 包含 可扩路
定义 为
则 是 的匹配,且 ,因而 就不是最大匹配
反之。。。。。。。。。。
偶图的匹配与覆盖问题的提出
问题的提出
在日常生活、工程技术中,常常遇到求偶图的匹配问题。例如:
有 7 名研究生 A,B,C,D,E,F,G 毕业寻找工作。就业处提供的公开职位是:会计师(a),咨询师(b),编辑(c),程序员(d),记者(e),秘书(f)和教师(g)。每名学生申请的职位如下:
A: b,c B: a,b,d,f,g C: b,e D: b,c,d E: a,c,d,f F: c,e G: d,e,f,g
问:学生能找到理想工作吗?
如果令 , 中的顶点与 中的顶点连线当且仅当学生申请了该工作
于是,得到反映学生和职位之间的状态图:
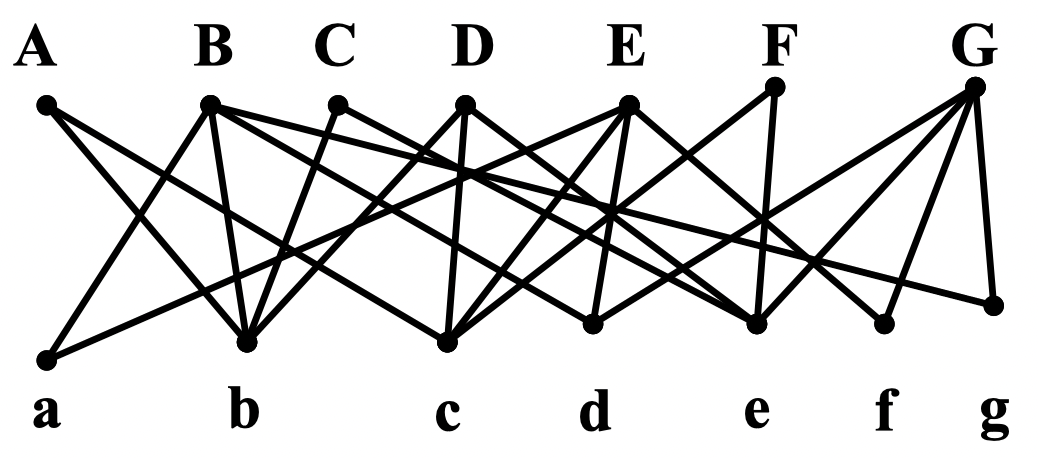
问题转化为求饱和 中每个顶点的一个匹配!!!
需要解决的问题是:
偶图的匹配存在性判定定理
定义 74:取图 的一个顶点子集 ,令 ,称 为 的邻集
例:在下图中,取 ,则
定理 60 (Hall 1935):设 为具有二分类 的偶图,则 包含饱和 的每个顶点的匹配当且仅当 对所有 成立
证明:
 注意
注意
- 存在饱和 每个顶点的匹配也常说成存在由 到 的匹配
- Hall 定理也称为婚姻定理:在一个由 个女生和 个男生构成的人群中 ,熟识的男女之间可能出现 对婚姻的充分必要条件是:对每个整数 ,任意 个女生共认识至少 个男生
- Hall 定理是在偶图中求最大匹配算法的理论基础,即匈牙利算法基础
推论:若 是 正则偶图 ,则 有完美匹配
证明: 是具有而分类 的 正则偶图
由于 是 正则的,所以 ,所以
任取 的一个子集 ,令
- 并且与的顶点关联
- 并且与的顶点关联
因与 中的顶点关联的边必与 中的顶点关联,所以我们可以推出
因此,,由此可知
根据 Hall 定理,可知 有一个饱和 的每个顶点的匹配 ,由于 ,所以 是完美匹配
例:
- 证明:每个 方体都有完美匹配
- 求 和 中不同的完美匹配的个数
证明:由 方体的构造知: 方体有 个顶点,每个顶点可以用长度为 的二进制码来表示,两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同
如果我们划分 方体的 个顶点,把坐标之和为偶数的顶点归入 ,否则归入
中顶点互不邻接, 中顶点也如此。所以 方体是偶图
很容易验证 方体的每个顶点度数为 ,所以 方体是 正则偶图
因此, 方体存在完美匹配
证明:我们用归纳法求 和 中不同的完美匹配的个数
的任意一个顶点有 种不同的方法被匹配
所以 的不同完美匹配个数等于 ,如此推下去,可以归纳出 的不同完美匹配个数为:
同样的方法可归纳出 的不同完美匹配个数为:
例:证明:非平凡树至多存在一个完美匹配
证明:若不然,设 与 是树 的两个不同的完美匹配,那么
容易知道: 的每个顶点度数为 2,即它存在圈,于是推出 中有圈,矛盾!
点覆盖与 König 定理
定义 75:图 的一个覆盖是指 的一个子集 ,使得 的每条边都至少有一个端点在 中
定义 76: 中点数最少的覆盖称为 的最小覆盖
例:
设 是 的覆盖, 是 的匹配,由于 中边互不相邻,若要覆盖 中的边,至少需要 个顶点,所以
特别地,若 是最大匹配,且 是最小覆盖,则
定理 61:设 是匹配, 的覆盖,若 ,则 是最大匹配,且 是最小覆盖
证明:设 是最大匹配, 是最小覆盖,则
由于 ,所以 ,
定理 62 (König 1931):在偶图中,最大匹配中的边数等于最小覆盖中的点数
证明:
例:矩阵的一行或一列统称为一条线。证明:包含一个 矩阵中所有 1 的线的最小条数,等于具有性质「任意两个 1 都不在同一条线上」的 1 的最大个数
证明:
Tutte 定理与完美匹配
图的分支根据它有奇数个或偶数个顶点而分别称为奇分支或偶分支,我们用 表示图 的奇分支的个数
定理 63 (Tutte):偶数阶图 有完美匹配当且仅当 ,对所有 成立
推论 (Peterson):每个没有割边的 3 正则图都有完美匹配
证明:
例:彼得森图满足推论的条件(即没有割边的 3 正则图),故它有完美匹配
 注:有割边的 3 正则图不一定就没有完美匹配
注:有割边的 3 正则图不一定就没有完美匹配
例:证明:树 有完美匹配当且仅当对所有顶点 ,
证明:必要性
因为 有完美匹配,由 Tutte 定理知
显然, 是偶数阶的图,于是
因此,
充分性
对于 的任意顶点 ,假设 是 的仅有的奇分支,且 与 之间的边为
显然
对于顶点 ,连接 与 的边也是
因此,对于任意的顶点 ,按照上述方式可以找到唯一的一个顶点与之配对
因为 , 具有偶数个顶点
从而, 的所有顶点都可以两两配对
因子分解
定义 77:图 的一个因子是指至少包含 的一条边的生成子图,即非空的生成子图就是一个因子
定义 78: 的一个因子分解是指将 分解成若干个边不重的因子之并
 注意
注意
- 每个因子必须包含图 的所有顶点 (生成子图)
- 因子分解的所有因子的并要等于图
定义 79:因子是指 正则的因子
解释:因子是指所有因子均是 正则图
例:
- 1-因子的边构成一个完美匹配
- 2-因子的连通分支为一个圈
定义 80:因子分解:每个因子均为 因子的因子分解,此时称 本身是 可因子化的
1-因子分解
若 有一个 1-因子 (其边集称为完美匹配),则显然 的阶数是偶数。所以,奇数阶图不能 1-因子分解
定理 64:完全图 是 1-可因子化的
证明:可由下法来确定 的 1-因子分解
把 的 个顶点编号为 。按照右图进行排列
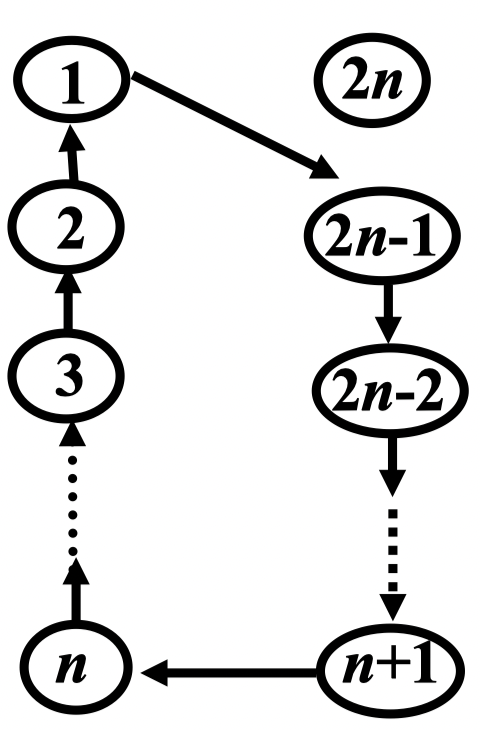
除 外,它们中的每一个数,按箭头方向移动一个位置;在每个位置中,同一行的两点邻接就得到一个 1-因子,共有 个不同的位置就产生了 个不同的 1-因子,从而完成了 的 1-因子分解
例:求 的 1-因子分解

定理 65: 正则偶图 是 1-可因子化的
证明:因正则偶图存在完美匹配,即 1-因子,从不断减去完美匹配的方式就可得到正则偶图的 1-因子分解
例:将 作 1-因子分解
解:将 中的点用数字 标记,而 中的点用 来标记,用排列 来表示 中的点与 的点之间的匹配关系,即
则:
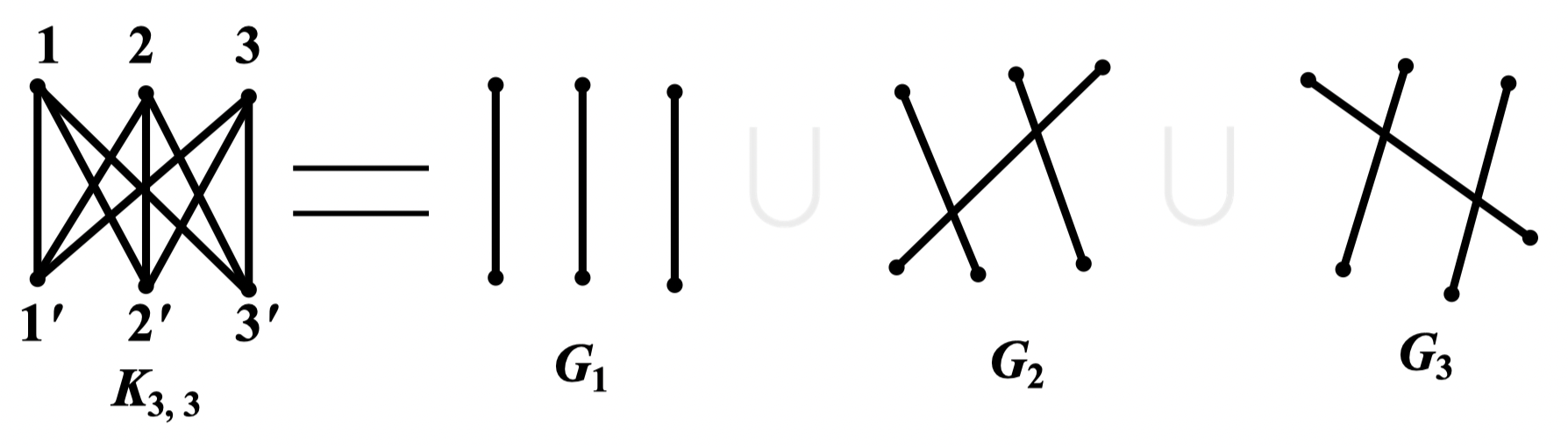
定理 66:具有 Hamilton 圈的 3 正则图是 1-可因子化的
证明:因为 是 3 正则图,故 的阶数是偶数
具有偶数个顶点的圈可以分解为两个 1-因子的并,得证
 注:1-可因子分解的 3 正则图不一定有 Hamilton 圈 (即:定理 66 返过来不一定成立)
注:1-可因子分解的 3 正则图不一定有 Hamilton 圈 (即:定理 66 返过来不一定成立)
例:下图是 3 正则图且可以 1-因子分解,但不存在 Hamilton 圈
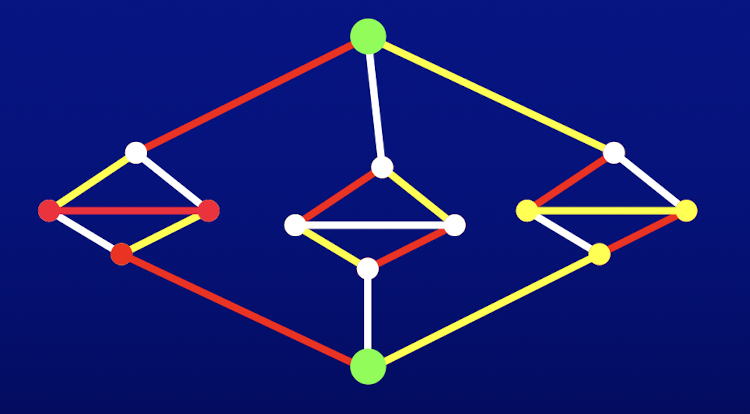
定理 67:若 3 正则图有割边,则不可 1-因子分解
证明:若 3 正则图 可以 1-因子分解,因去掉 的不含割边的 1-因子后,途中每个点均为 2 度,从而每条边均在圈中,特别地割边也在圈中,矛盾!!
 注:无割边的 3 正则图可能也没有 1-因子分解
注:无割边的 3 正则图可能也没有 1-因子分解
例:假设彼得森图可以分解成三个 1-因子 的并
证明:假设彼得森图可以分解成 3 个 1-因子 的并
和 一定均包含圈 ,否则存在两条相邻的边出现在同一个 1-因子中
假设边 ,则 和 一定不属于
因为 不属于 ,则 和 中的某一条必然属于
同理, 和 中某一条必然属于
因此, 恰好包含圈 上的两条边
类似的, 和 也恰好包含圈 上的两条边。矛盾!!!
例:证明: 有唯一的 1-因子分解
证明:因为 只有 3 个不同的完美匹配,而 的每个 1-因子分解包含 3 个不同的完美匹配,所以,其 1-因子分解唯一
| | | | | |
|---|
| 1 | 1 | 6 | 6240 | 1225566720 | 252282619805368320 |
的 1-因子分解的数目为
例:对任意的 ,构造一个没有 1-因子的 正则图
解:
2-因子分解
由定义有:
- 每个 2-因子是边不重圈的并
- 若一个 2-因子是连通的,则它是一个 圈
- 2-可因子化的图的所有点的度一定是偶数,所以完全图 不是 2-可因子化的
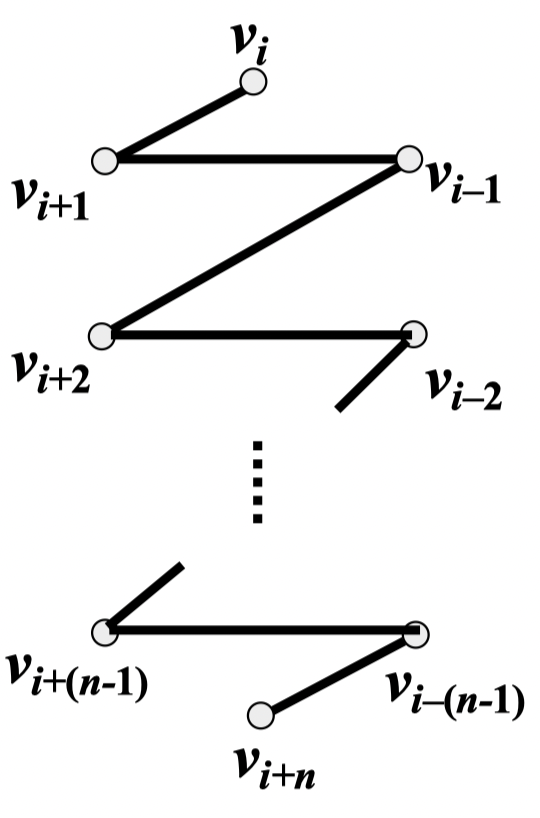
定理 68:图 是 个 圈的并
证明:为了在 中构造 个边不重的 圈,先标定它的点
然后,在点 上构造 条路 如下:
并且所有下标取为整数
Hamilton 圈 是由 联接于 的两个端点构成
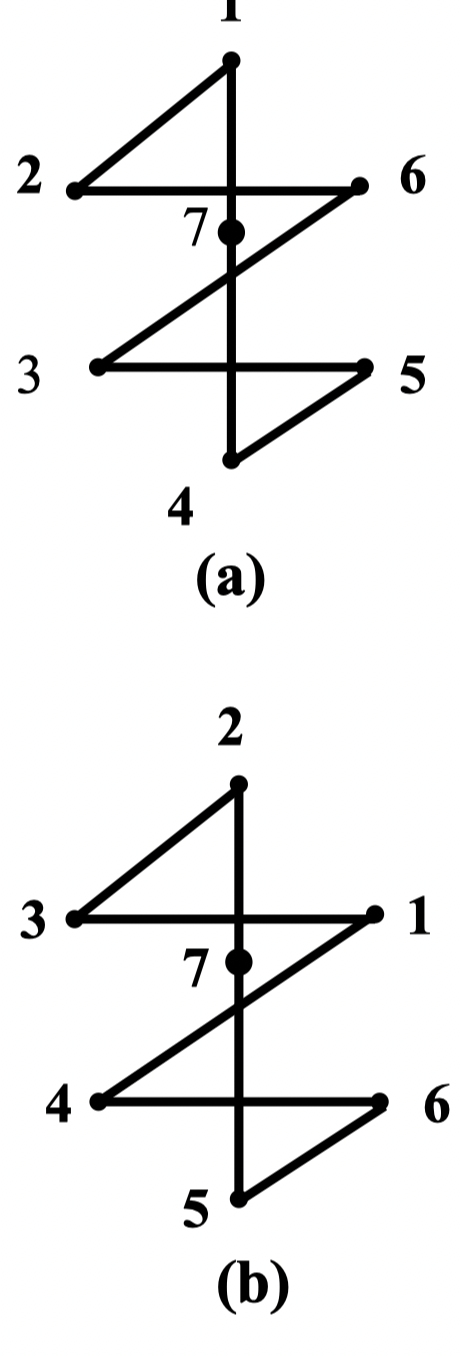
例:将 分解成 3 个 圈的并
解:将 的顶点用数字 表示,而 为正六边行的顶点, 是中心
图 (a) 中,实线部分就是一个 2-因子,它是一个 圈:
若将 绕中心按顺时针方向移动一个位置,见图 (b),则得另一个 圈:
第三个 圈必然是
则
定理 69:完全图 是一个 1-因子和 个 圈的并
证明:设
作 条路:
并且所有下标取为整数
然后把 和 的两个端点联接,得到 个 圈
去掉 个 圈后,剩下的边构成一个 1-因子
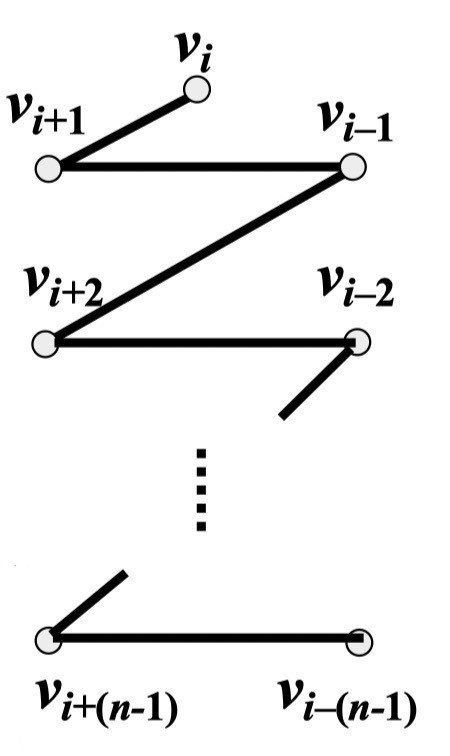
例:将 分解为一个 1-因子和 2 个 圈的并
解:
则 可分解为
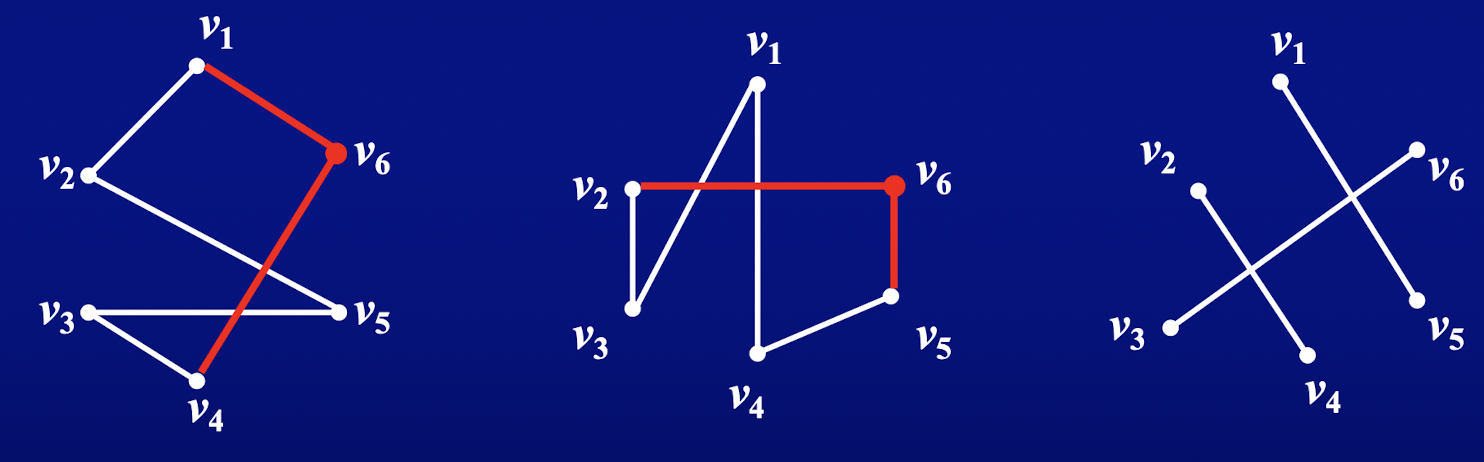
定理 70:每一个没有割边的 3-正则图是一个 1-因子和一个 2-因子的并
证明:因每个没有割边的 3-正则图存在完美匹配 ,显然, 是一个 2-因子
例:彼得森图是一个 1-因子和一个 2-因子的并
 注:若没有割边的 3-正则图中的 2-因子是一些偶圈,则该图也是 1-可因子化的
注:若没有割边的 3-正则图中的 2-因子是一些偶圈,则该图也是 1-可因子化的
定理 71:一个连通图是 2-可因子化的当且仅当它是偶数度正则图
证明:
例:给出图 的一种 2-因子分解
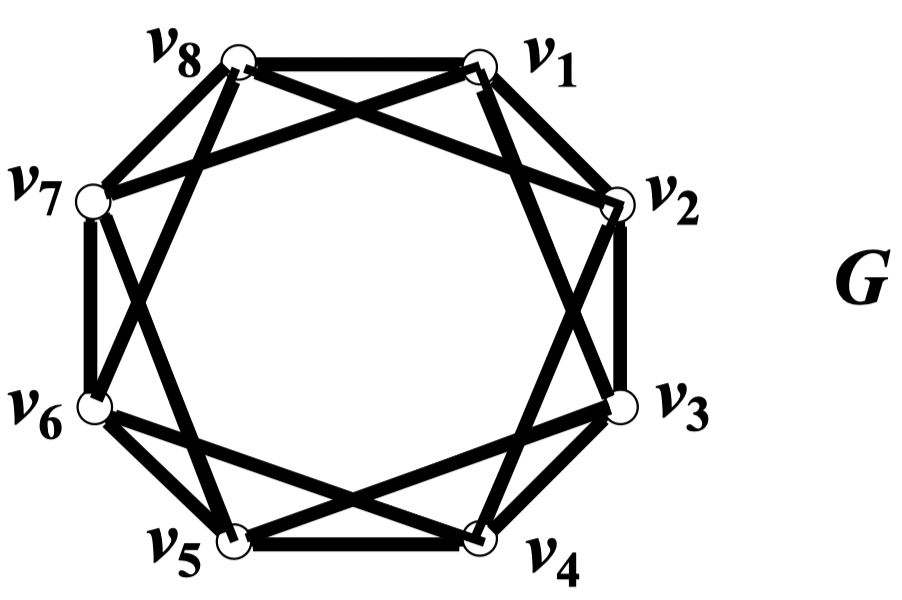
解:
森林分解
定义 81:把一个图分解为若干个边不重的森林因子的并,称为图的森林因子分解,简称森林分解
定义 82:无环图 分解为边不重的生成森林的最少数目,称为图 的荫度,记为
 注:所有森林因子的并要等于图
注:所有森林因子的并要等于图
例:
定理 72:令 是一个非平凡图,设 是 的最大的 阶子图所包含的边数,则 。对于 , 的最大值显然在 时出现,所以 。对完全偶图 , 的最大值在
推论:完全图和完全偶图的荫度为
完全图的森林分解方法
- 将 分解成 条生成路
- 在 分解得到的每条生成路上附加一个标号为 的孤立点,然后连接 与另外 个点构成一个星形图
例:分 为生成森林的最小分解如下图所示
 (考过) 例:证明:若 为偶数且 ,则 阶图 有 3-因子
(考过) 例:证明:若 为偶数且 ,则 阶图 有 3-因子
证明:因 ,由 Dirac 定理得: 阶图 有 圈
又因 为偶数,所以 为偶圈
于是由 可得到 的两个 1 因子,设其中一个为
考虑 ,则 。于是 中有 圈
作 。显然 是 的一个 3-因子
思考:若 为 阶简单图 ( 为偶数) 且 ,则 中存在 5-因子
思考:当 时,完全图 可以 4-因子分解
最优匹配 & 匈牙利算法 (几乎不考)
人员分派问题: 个工人 , 件工作 。已知 能胜任某 件工作 。问能否存在一种工作安排方案,使每个人都能分配到他所能胜任的一件工作(假定每件工作只能一人做)。若能,又如何安排?
图论模型:以工人和工作为点,当且仅当 能胜任工作 时则连线,得偶图 。于是一种符合要求的安排对应 中一个完美匹配。次问题实际上是 求偶图的完美匹配问题
若不要求人数与工作数相等,则问题是求偶图的饱和 的每个点的匹配问题,其中 是工人的集合
进一步,若问:能否存在一种安排使尽可能多的人能分到他能胜任的工作或使尽可能多的工作被分配,则问题为 求偶图的最大匹配问题
匈牙利算法 (几乎不考)
算法思想:先任取一个匹配 ,然后寻找 可扩路。若不存在 可扩路,则 为最大匹配;若存在,则将可扩路中 与非 的边互换,得到一个比 多一条边的匹配 ,再对 重复上面过程
算法是从 的每个非饱和点出发寻找 可扩路的。若从 的每个非饱和点出发都无 可扩路,则 必无可扩路,从而 是最大匹配。这是因为偶图中不可能存在两个端点均在 中的 可扩路
定义 83:设 是 中的匹配, 是 的 非饱和点,若树 满足:(1) ;(2) 对 的每个顶点 , 中唯一的 路是一条 交错路,则称树 是一棵扎根于 的 交错树
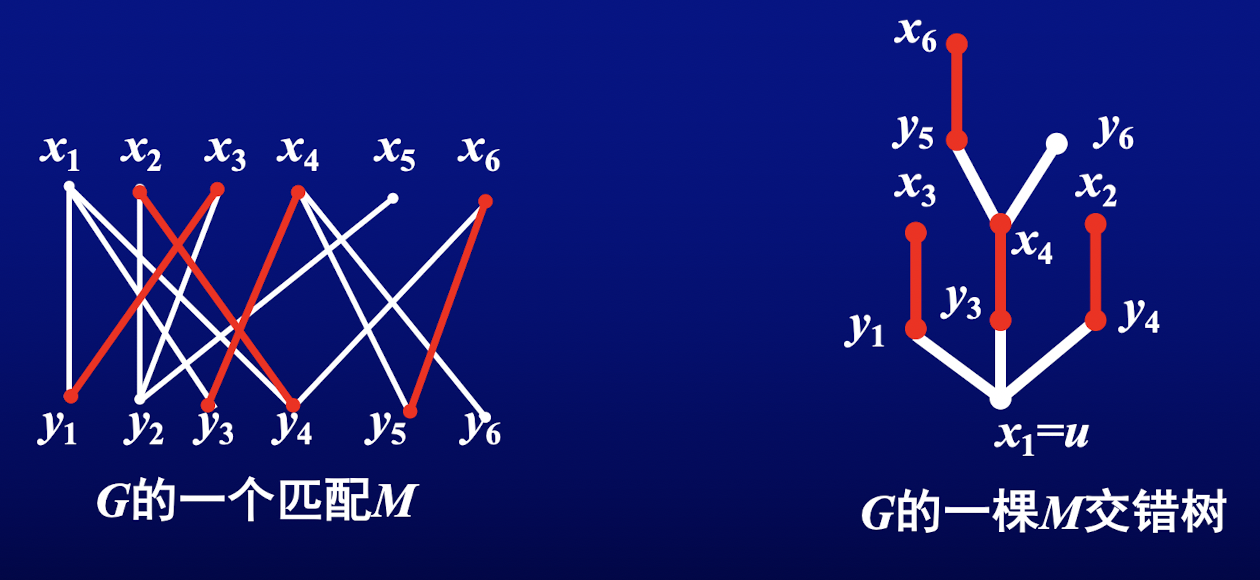
算法中,寻找以 为起点的一条 可扩路,其过程包含「生长」一棵扎根于 的 交错树
开始时, 仅由单一顶点 组成,而在以后的步骤中它都按以下方式生长:
- 除 以外的所有其他顶点都是两两配对的 饱和点,如图 (a)
- 包含不同于 的非 饱和顶点,如图 (b)
若始终是图 (a) 的情况,则无 可扩路;若出现图 (b) 的情况,则找到了 可扩路
对于情形 1,令 ,显然:
若 ,由于 中的点与 中的点配对,所以 。因此
由 Hall 定理知, 中不存在可以饱和 中所有顶点的匹配
若 ,则在 中存在点 与 中点 相邻
若 ,由于 是 非饱和点,所以 。若 ,由于 中除 之外的点均是 饱和点,所以
如果 是 饱和的,假定 ,则添加点 和 以及边 和 来生长 ,然后回到情形 1
如果 是 非饱和的,则添加点 和边 来生长 ,结果得到情形 2
匈牙利算法步骤:给定具有而分类 的偶图
- (1) 任取一个匹配
- (2) 若 中每个点均为 饱和点,则停,输出 ;否则转 (3)
- (3) 取 的饱和点 ,令
- (4) 若 ,此时由于 ,所以 ,若求饱和 中每个点的匹配,则停止 (问题无解);若求最大匹配,则将 也作为 饱和点对待,转 (2);否则取
- (5) 若 为饱和点,则转 (6);否则转 (7)
- (6) 存在 ,有 ,令 ,,转 (4)
- (7) 存在 到 的 可扩路 ,令 ,转 (2)
例:求图 (图(a)) 的最大匹配,其中
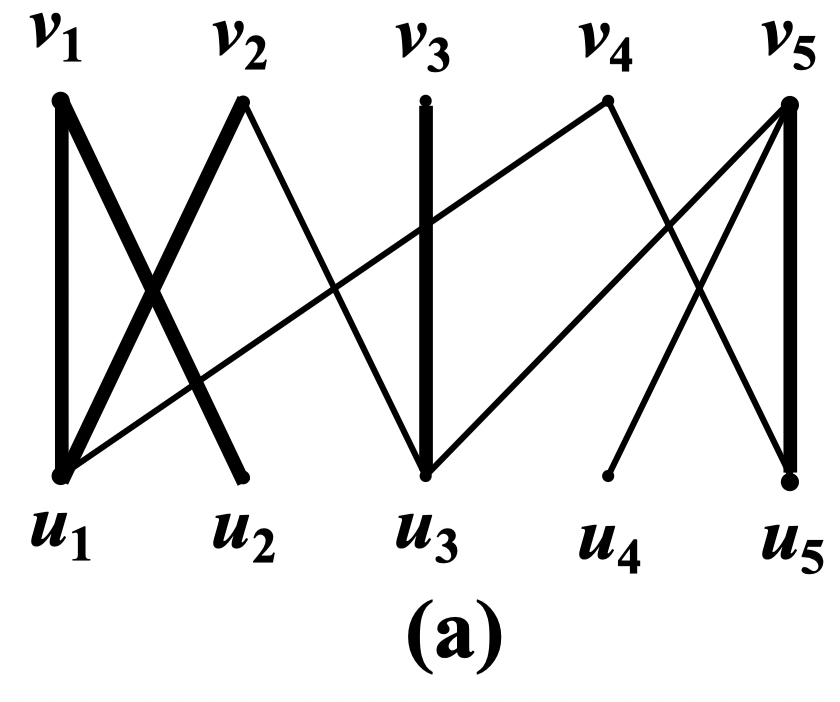
任取一个匹配 ,如图 (a) 的红色所示
中存在非饱和点,取其中一个 ,令
最优匹配 (几乎不考)
设 是一个边赋权完全偶图,其中 ,,边 的权 表示工人 做工作 时的效率。最优分派问题指的是在赋权完全偶图中寻找一个具有最大权值的完美匹配,称为最优匹配
定义 84:设 ,若在顶点集上的实值函数 满足:对任意的 均有:,称 是赋权完全偶图 的可行顶点标号
对于任意的赋权完全偶图 ,均存在 的可行顶点标号。事实上,设:
则 是 的一个可行顶点标号
定义 85:设 是赋权完全偶图 的可行顶点标号,令:,称以 为边集的 的生成子图为 的对应于 的相等子图,记为
例:设如下矩阵是赋权完全偶图 的权值矩阵并注明了一种可行顶点标号
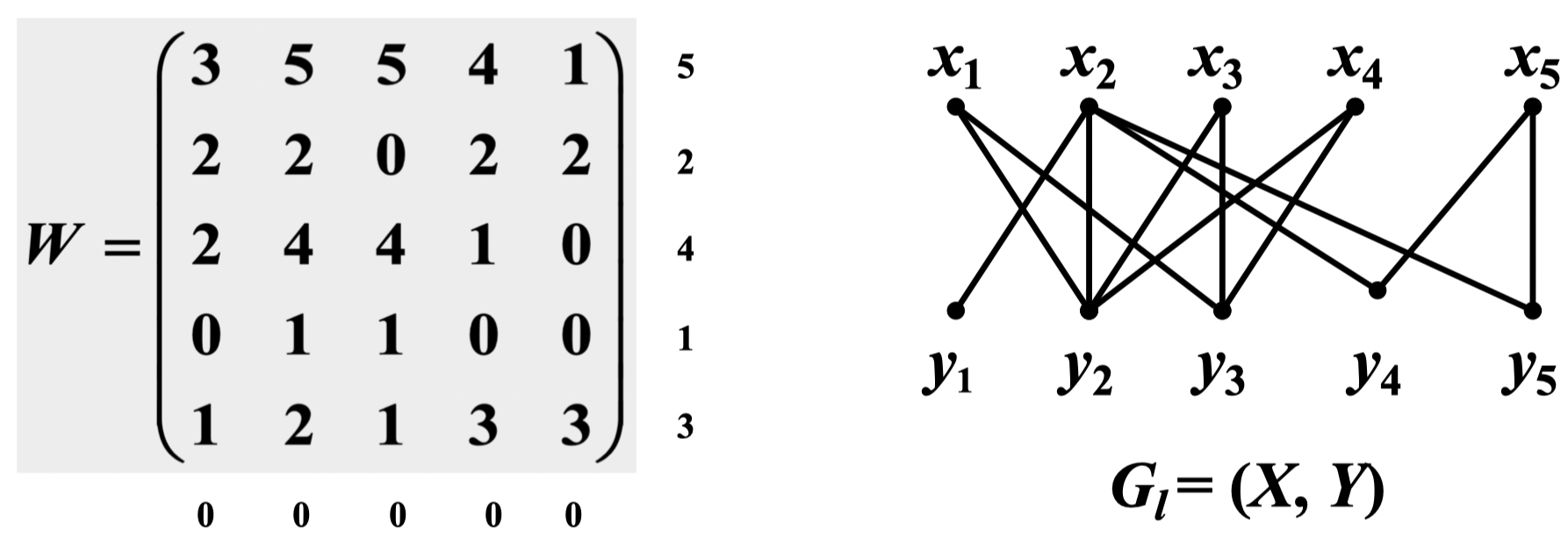
定理 73:设 是赋权完全偶图 的可行顶点标号,若相等子图 有完美匹配 ,则 是 的最优匹配
证明:设 是 的完美匹配,则:
又设 是 的任一完美匹配,则:
所以,,即 是 的最优匹配
算法基本思想:首先给出任一可行顶点标号 ,然后决定 ,在 中选取任一匹配 ,再利用匈牙利算法。若在 中已找到一个完美匹配,则该匹配就是最优匹配。否则修改可行顶点标号,直到完美匹配在某个相等子图中找到为止
Kuhn-Munkres 算法:给定一初始顶点标号 ,在 中任选一个匹配
若 是 饱和的,则 是最优匹配。否则,令 是一个 非饱和点,置
若 ,转 3。否则,计算:
根据 给出新的可行顶点标号,在新标号下重新开始
在 中选择点 。若 是 饱和的,且 ,则置 ,转 2。否则,设 是 中 可扩 路,置 ,转 1
例:给定赋权完全偶图 的权值矩阵,求其最优匹配
解:
匹配在矩阵理论中的应用
定理 74: 阶方阵 的行列式展开式中每一项均为零的充要条件是存在 ,使 有一个 阶的子矩阵,它的所有元素均为零
证明:
第六章 平面图
平面图的概念
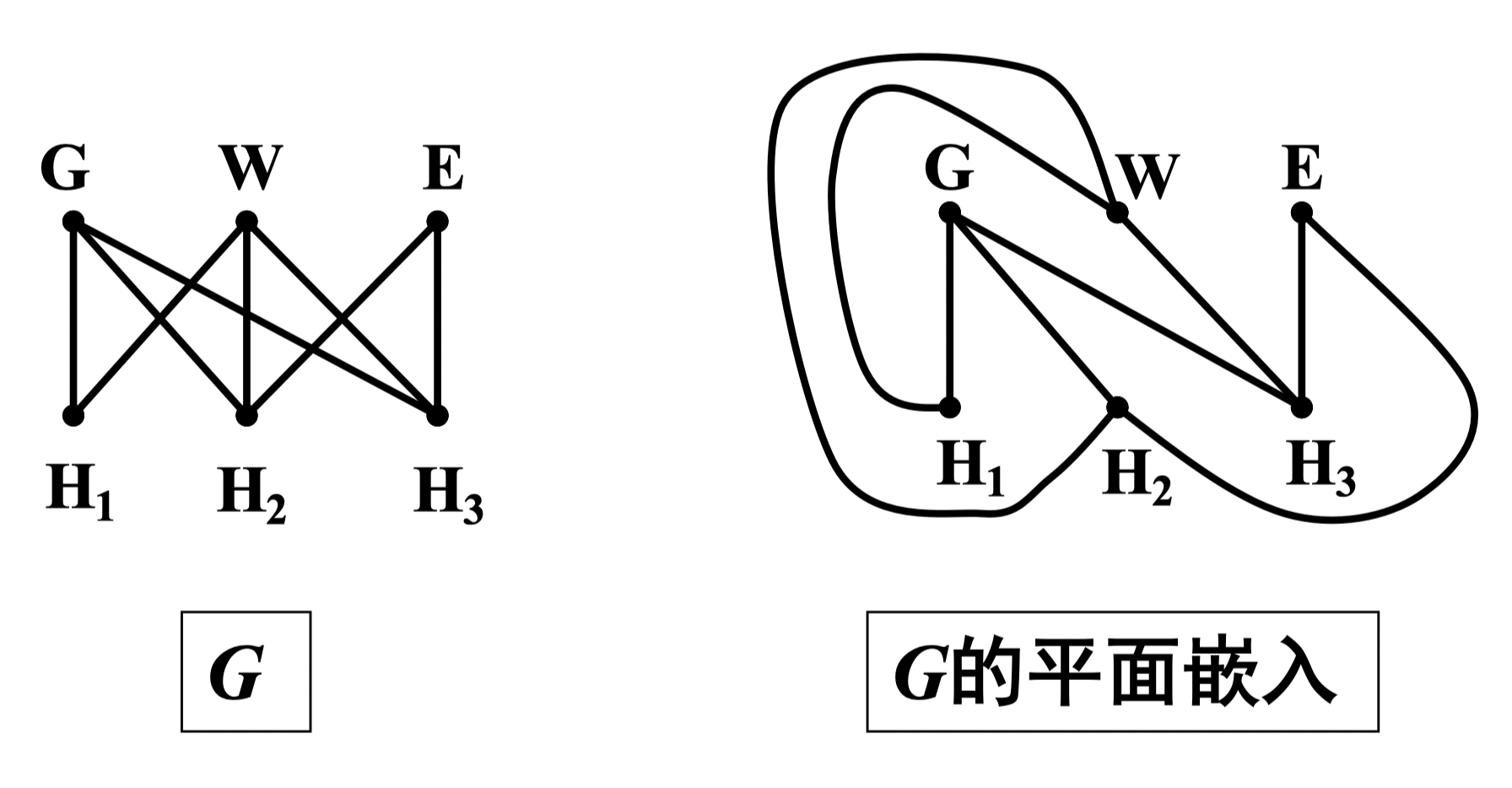
定义 86:设图 可画在一个平面上使除顶点外边不交叉,则称 可嵌入平面,或称 为可平面图。可平面图 的边不交叉的一种画法称为 的一个平面嵌入, 的平面嵌入表示的图称为平面图
 注:可平面图概念和平面图概念有时可以等同看待
注:可平面图概念和平面图概念有时可以等同看待
例:
平面图的性质
定义 87:设 是一个平面图, 将所嵌入的平面划分为若干个区域,每个区域的内部连同边界称为 的面,无界的区域称为外部面或无限面。 的面组成的集合用 表示
 注:每个平面图有且仅有一个外部面
注:每个平面图有且仅有一个外部面
例:
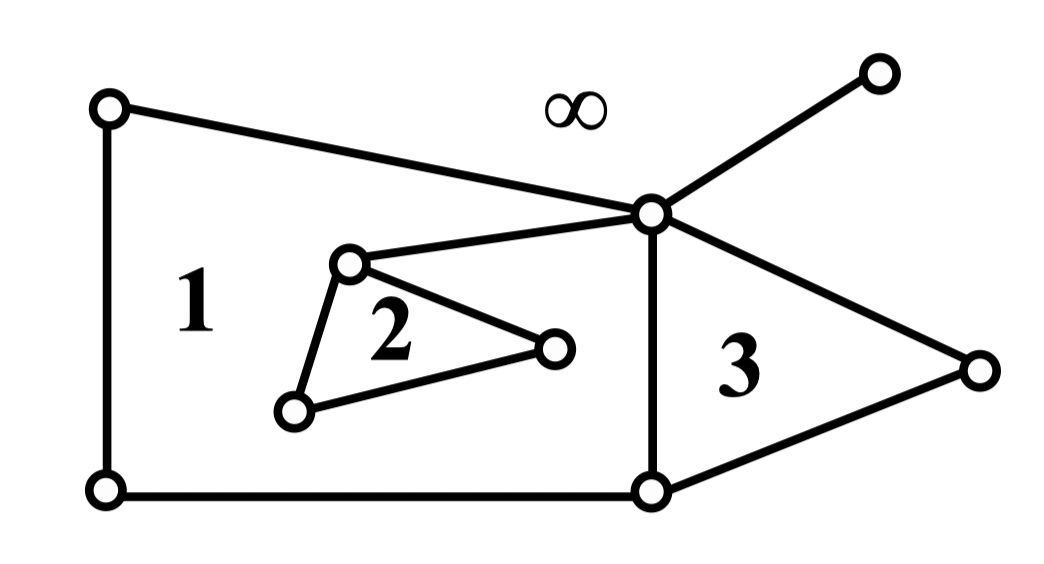
定义 88:设 是 一个面,构成 的边界的边数 (割边计算两次) 称为面 的次数,记为
例:有 5 个面:
 注意
注意
- 中存在一条割边,需要计算两次
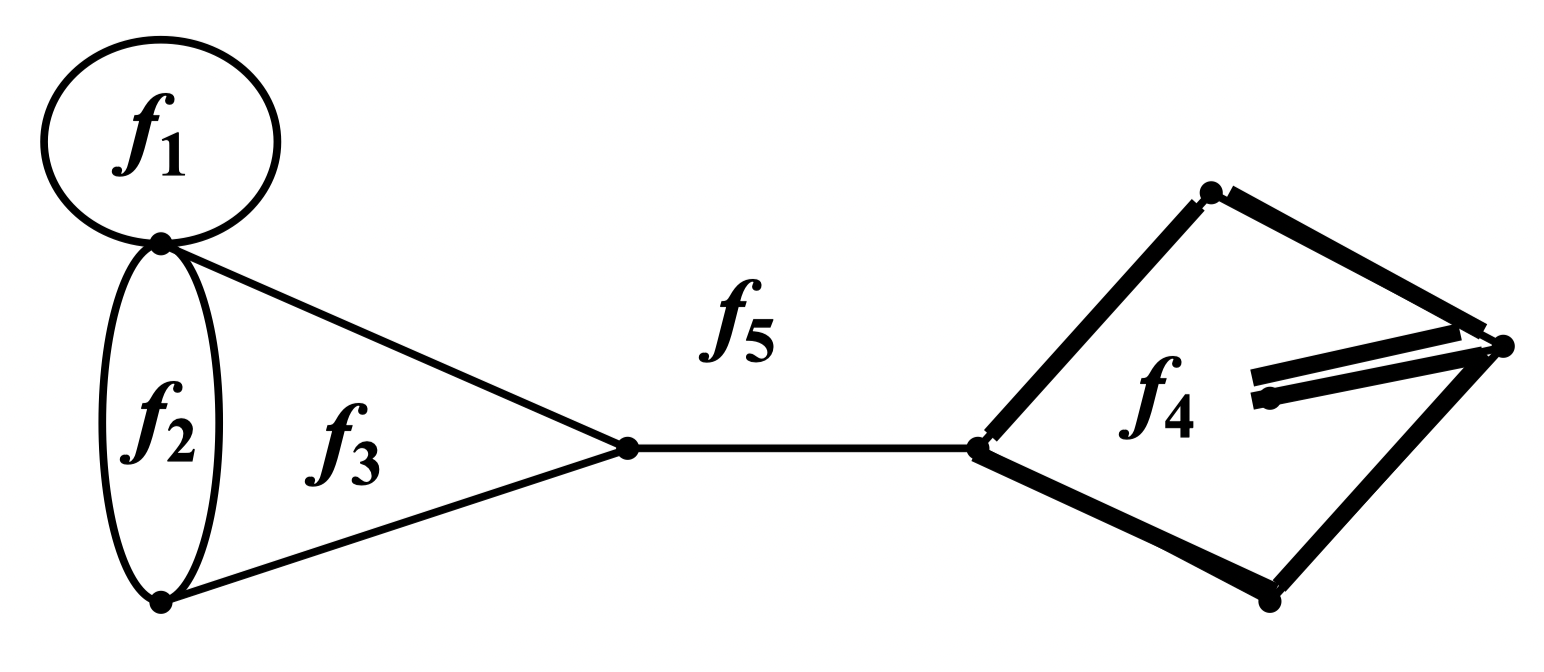
例:图不连通,其外部面的次数为 5 (存在割边)
定理 75:设 是具有 条边的平面图,则
证明:对 的任意一条边 ,如果 是某面的割边,那么由面的次数定义,该边给 的总次数贡献 2 次;如果 不是割边,那么它必然是某两个面的公共边,因此,由面的次数定义知,它也给总数贡献 2 次。于是结论成立
定理 76 (Euler 公式):设 是具有 个点, 条边, 个面的连通平面图,则有
证明:对 用归纳法
当 时, 无圈又连通,从而是树,有
于是
设 时,结论成立
当 时,此时 至少两个面,从而有封闭的面
删去 与另一个面的一条公共边,记所得之图为 。并设 的点数、边数和面数依次为 , 和 ,易知 仍连通,但只有 个面
由归纳假设知,
同时,
由关系式 可得,
推论:设 是具有 个点, 条边, 个面, 个连通分支的平面图,则
证明:设 是 个连通分支分别为 ,对每个 用欧拉公式得:,其中 分别为 的点数、边数和面数
将 个等式两边相加得:
而:
所以:
推论:设 是具有 个点, 条边, 个面, 个连通分支的平面图,如果对 的每个面 ,有 ,则
证明:一方面,
另一方面,由欧拉公式得:
所以:
整理得:
 注意
注意
- 上面的推论也可以叙述为:设 是具有 个点, 条边的连通图,如果 ,则 是非可平面图
- 推论的条件是 「 是平面图」的必要条件,不是充分条件
例:求证: 是非可平面图
证明:注意到, 是偶图,不存在奇圈,所以,每个面的次数至少是 4,即
所以
而 ,因此与 ,矛盾!
所以, 是非可平面图
推论:设 是具有 个点, 条边的简单平面图且 ,则
证明:情形 1: 连通
因为 是简单图,所以每个面的次数至少为 3。于是,
情形 2: 不连通
若 存在至少有三个点的连通分支,因为对 的这些连通分支,结论成立。将各不等式相加也得类似不等式,设为
再设 的所有少于 3 个点的连通分支的总边数为 ,总点数为
此时有 ,于是
从而有
若 没有多于两个点的连通分支。此时
因 时,,所以有
例:证明: 是非可平面图
证明: 是简单图,且 。因此 ,与结论「」相矛盾!所以 是非可平面图
推论:设 是具有 个点, 条边的简单平面图,容 中所有面均由长度为 的圈围成,则
定理 77:设 是简单平面图,则
证明:对点数 的情况,直接验证可知结论成立
设 ,若 ,则
这与「」矛盾!
定理 78:一个连通平面图 是 2 连通的当且仅当 的每个面的边界是圈
证明:由于环不影响图的连通性与平面性,故假设所讨论的图无环
「必要性」
。。。。
「充分性」
。。。。。
推论:设一个平面图是 2 连通的,则它的每条边恰在两个面的边界上
平面嵌入概念的推广
定义 89:若图 能画在曲面 上使它的边仅在端点相交,则称图 可嵌入曲面 ;图 的这样一种画法 (若存在的话) 称为 的一个 嵌入
例:下图表示 的环面嵌入,其中矩形的两对对边相等同
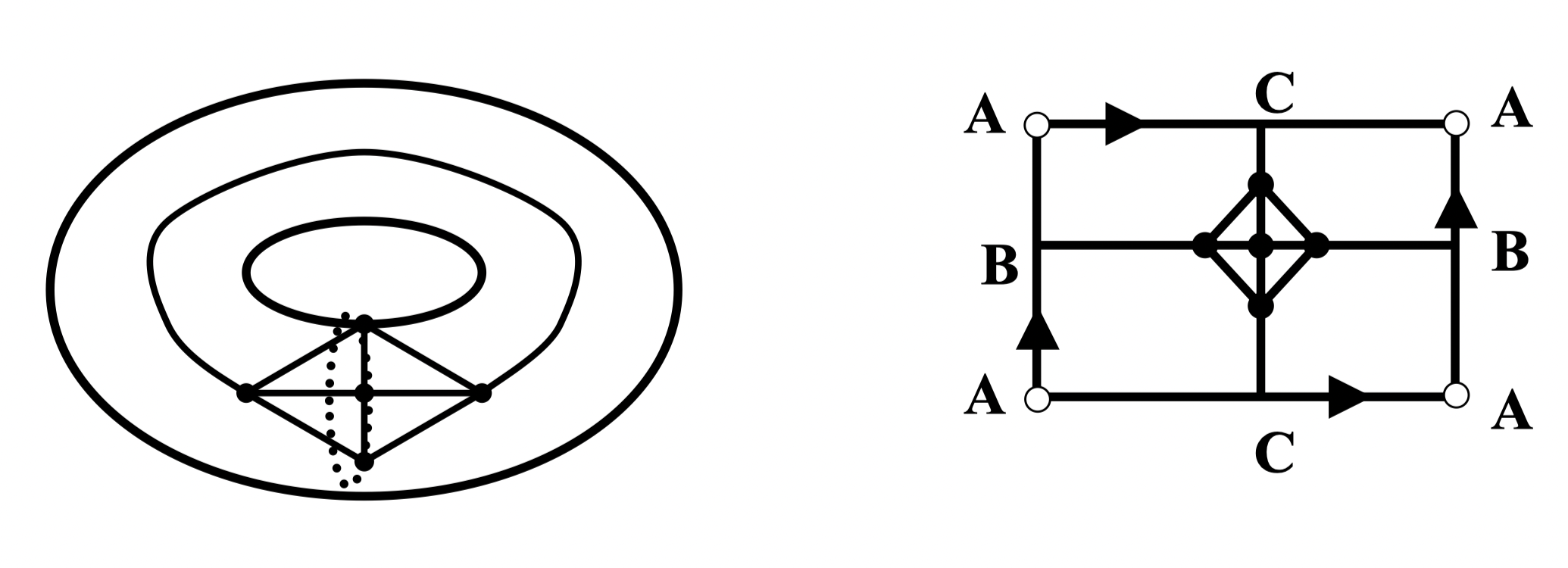
 注意
注意
- 不可嵌入平面,但能嵌入环面,也存在不可嵌入环面的图
- 可以证明对每个曲面 总存在不可嵌入 的图。另一方面每个图又存在可以嵌入的某个可定向的曲面
定理 79:一个图可嵌入平面当且仅当它可嵌入球面
证明:
凸多面体与平面图
如果将一个有 个顶点, 条棱和 个面的凸多面体的顶点作为顶点,棱作为边,则这个多面体可视为一个图 ,很明显 可嵌入球面,从而可嵌入平面而得到一个连通的平面图。因而凸多面体的顶点数,棱数与面数也满足 。这个公式也称为欧拉公式
定理 80 (Platonic):存在且只存在 5 种正多面体:正四面体、正六面体、正八面体、正十二面体和正二十面体
证明:任取一个正 面体 ,设 有 个顶点, 条棱
将 嵌入平面记所得的平面图为 。易知 是一个每个面的次数均相同 (设为 ) 的 度简单正则图
从而有
因此
将上两式代入欧拉公式 得
整理得,,即
所以,
因 和 均为正,所以 。因此
这样我们得到不等式组
此不等式组的整数解恰为 5 组。根据这 5 组解可求得相应的 值,其结果见下表:
| 序号 | | | | | | 相应的正对面体 |
|---|
| 1 | 3 | 3 | 4 | 6 | 4 | 正四面体 |
| 2 | 3 | 4 | 8 | 12 | 6 | 正六面体 |
| 3 | 3 | 5 | 20 | 30 | 12 | 正十二面体 |
| 4 | 4 | 3 | 6 | 12 | 8 | 正八面体 |
| 5 | 5 | 3 | 12 | 30 | 20 | 正二十面体 |
极大平面图及其性质
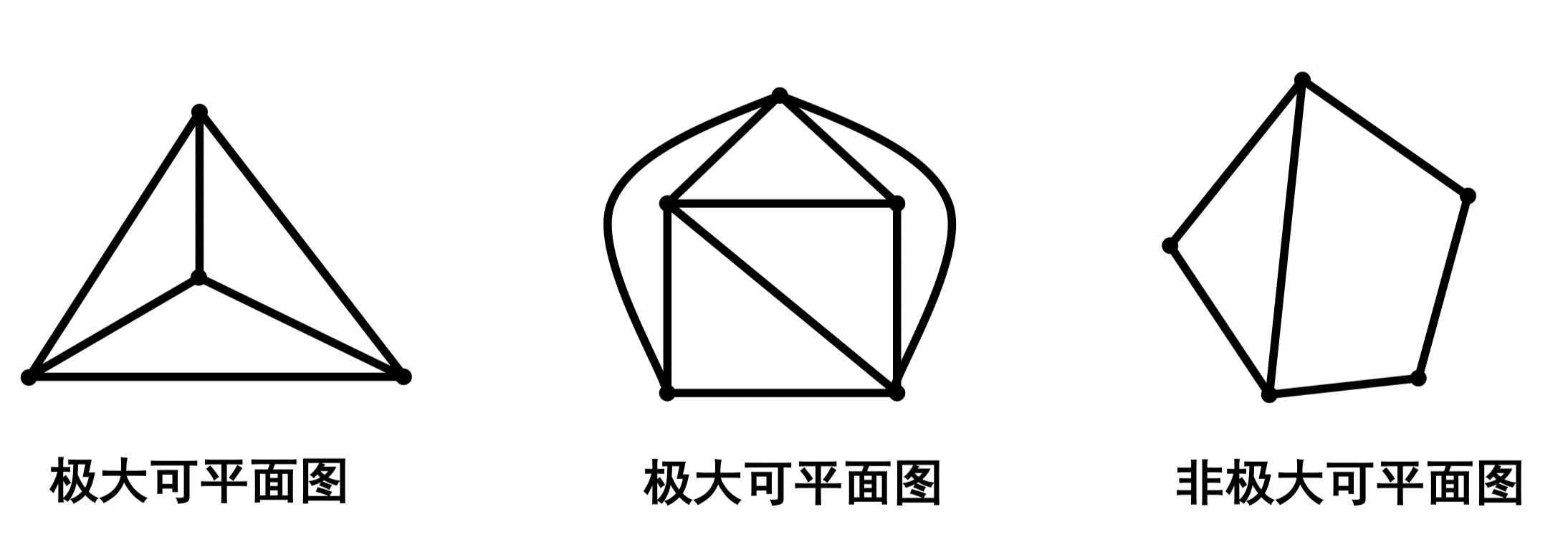
定义 90:设 是简单可平面图,如果 是 ,或者在 的任意两个不相邻的顶点间添加一条边后,得到的图均不是可平面图,则称 是极大可平面图。极大可平面图是平面嵌入称为极大平面图
例:
引理:设 是极大平面图,则 必连通;若 的阶数至少等于 3,则 无割边
证明:
定理 81:设 是至少有 3 个顶点的平面图,则 是极大平面图的充分必要条件为 中各面次数均为 3 且为简单图
证明:
 注:该定理可以简单记为「极大平面图的三角形特征」,即每个面的边界是三角形
注:该定理可以简单记为「极大平面图的三角形特征」,即每个面的边界是三角形
推论:设 是一个有 个点, 条边, 个面的极大平面图,且 ,则 (1) ;(2)
推论表明对一个极大平面图 ,当其点数 给定时, 的边数和面数也就确定了,从而 的结构框架也大体确定了
例如:当 时, 为 ;当 时, 为正八面体图
当 时, 有 21 条边,14 个面,其中一个结构如图所示:
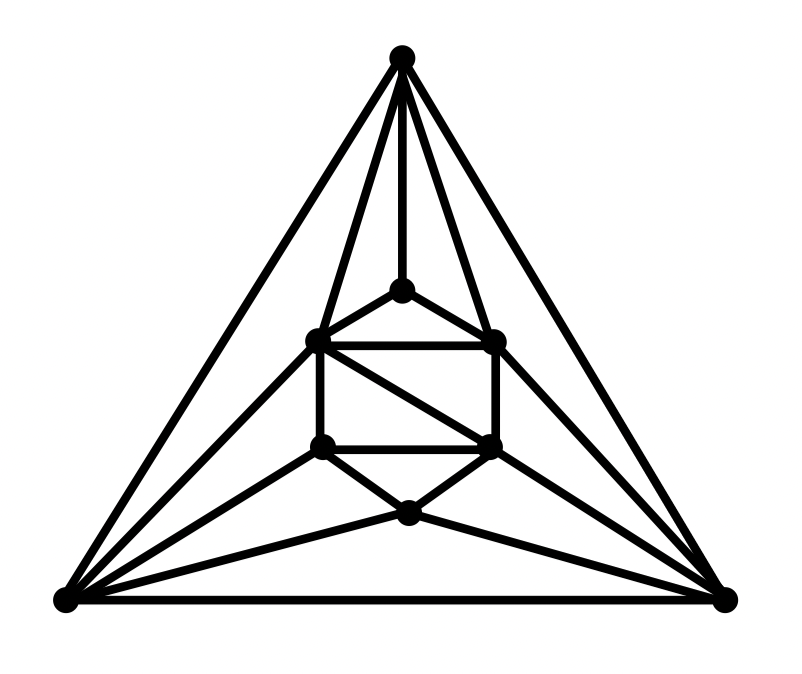
当 时, 有 30 条边,20 个面,此时,其中一个为正二十面体图,另一个如图所示
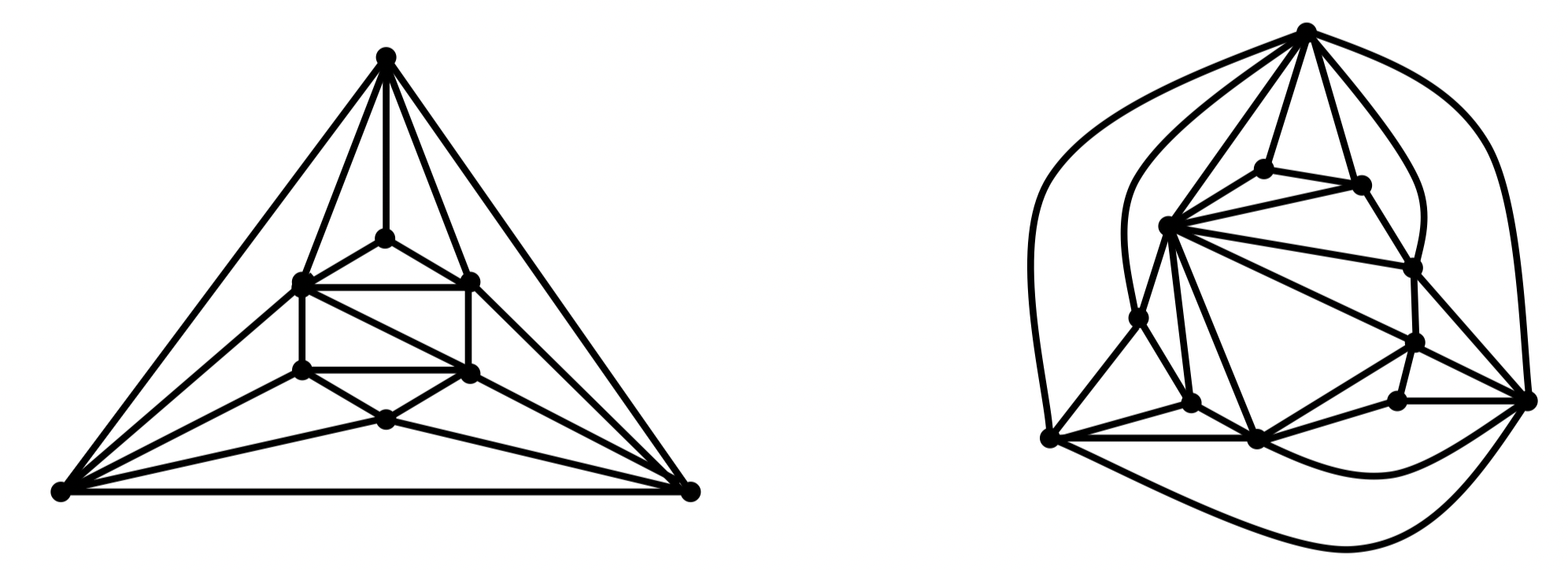
 注:顶点数相同的极大平面图并不唯一。顶点数相同的极大平面图的个数和结构问题仍在研究当中
注:顶点数相同的极大平面图并不唯一。顶点数相同的极大平面图的个数和结构问题仍在研究当中
与「极大可平面图」相对应地图是「极小不可平面图」
定义 91:如果在不可平面图 中任意删去一条边所得的图为可平面图,则称 为极小不可平面图。例如 和
极大外平面图及其性质
定义 92:若一个可平面图存在一个所有顶点均在同一个面的平面嵌入,则称该图为外可平面图。外可平面图的任一外平面嵌入 (即所有顶点均在同一个面的嵌入) 称为外平面图
例:下图给出了一个外可平面图及两种外平面嵌入
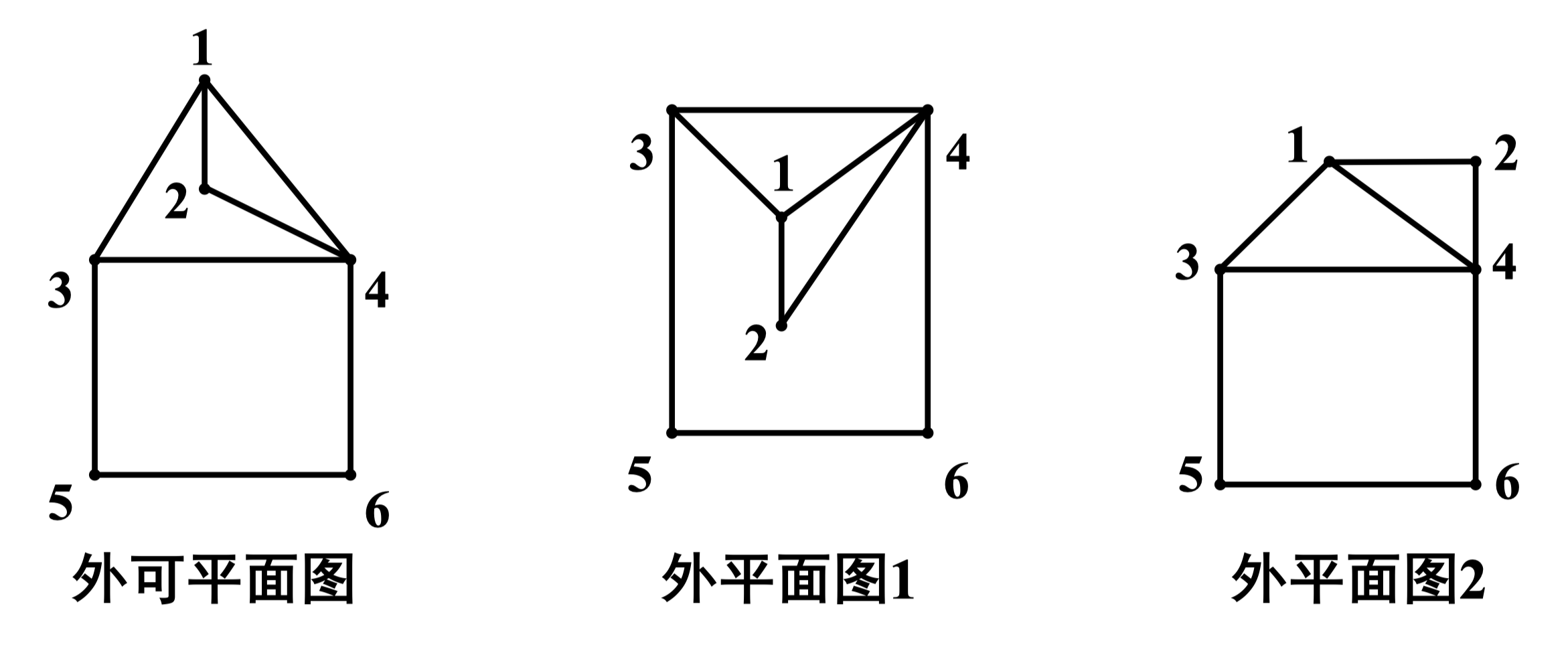
 注:对外可平面图 来说,一定存在一种外平面嵌入,使得 的顶点均在外部面的边界上
注:对外可平面图 来说,一定存在一种外平面嵌入,使得 的顶点均在外部面的边界上
定义 93:设 是简单外可平面图,若在 中任意不邻接顶点间添上一条边后, 成为非外可平面图,则称 是极大外可平面图。极大外可平面图的外平面嵌入称为极大外平面图
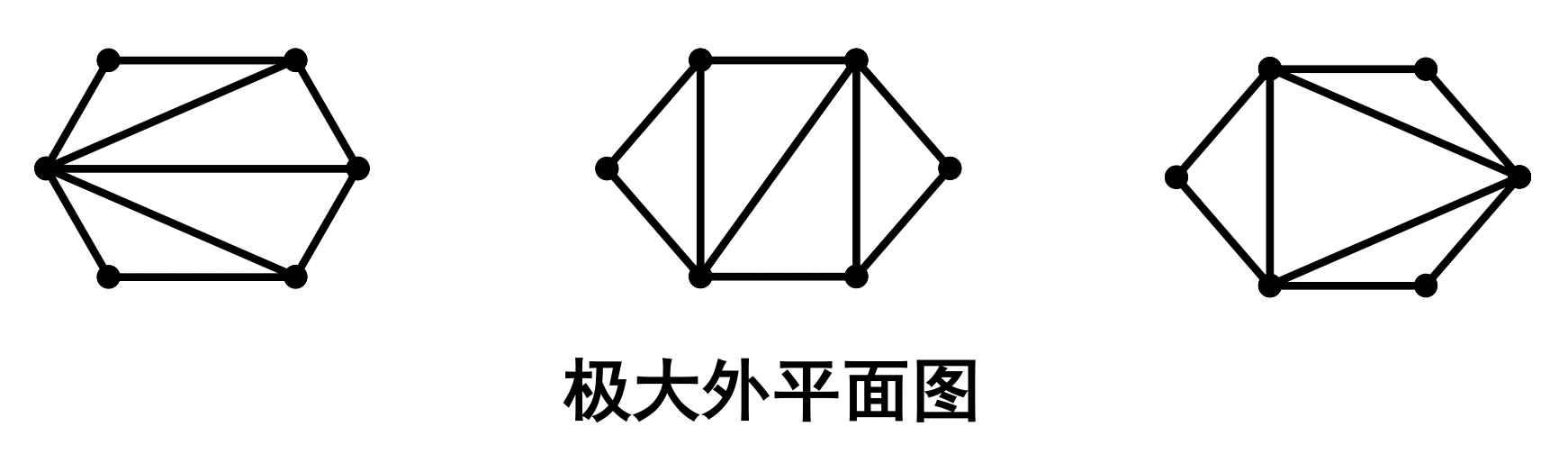
 注:极大外平面图的外部面的边界是由多边形组成,内部面均由三角形围成
注:极大外平面图的外部面的边界是由多边形组成,内部面均由三角形围成
定理 82:设 是一个有 个点,且所有点均在外部面上的外平面图,则 是极大外平面图当且仅当其外部面的边界是圈,内部面是三角形
证明:
引理:设 是一个阶数为 且所有点均在外部面上的极大外平面图,则 中存在两个度数均为 2 且不相邻的点
证明:
定理 83:设 是一个有 个点,且所有点均在外部面上的极大外平面图,则 有 个内部面
证明:
例:设 是一个具有 个点, 条边的简单连通外平面图。若 不含三角形,则
证明:假设 的所有顶点在外部面的边界上,则由条件知: 的外部面的次数至少为 ,内部面的次数至少为 4
设 有 个面,则
由欧拉公式得:
因此,根据上述两式得:
定理 84:每个至少有 7 个顶点的外可平面的补图不是外可平面图,且 7 是这个数目的最小者
对偶图
定义 94:给定平面图 , 的对偶图 是如下构造的图:
- 在 的每个面 内任取一点 作为 的顶点
- 对 的每条边 ,若 是面 与 的公共边时,则连接 与 ,得 的边 ,并使 与 相交;若 只在一个面 上时,则以 为顶点作环,得 的边 ,并使 与 相交
例:在下图中,平面图如 (a) 所示,其对偶图如 (b) 所示,其构造过程如 (c) 所示
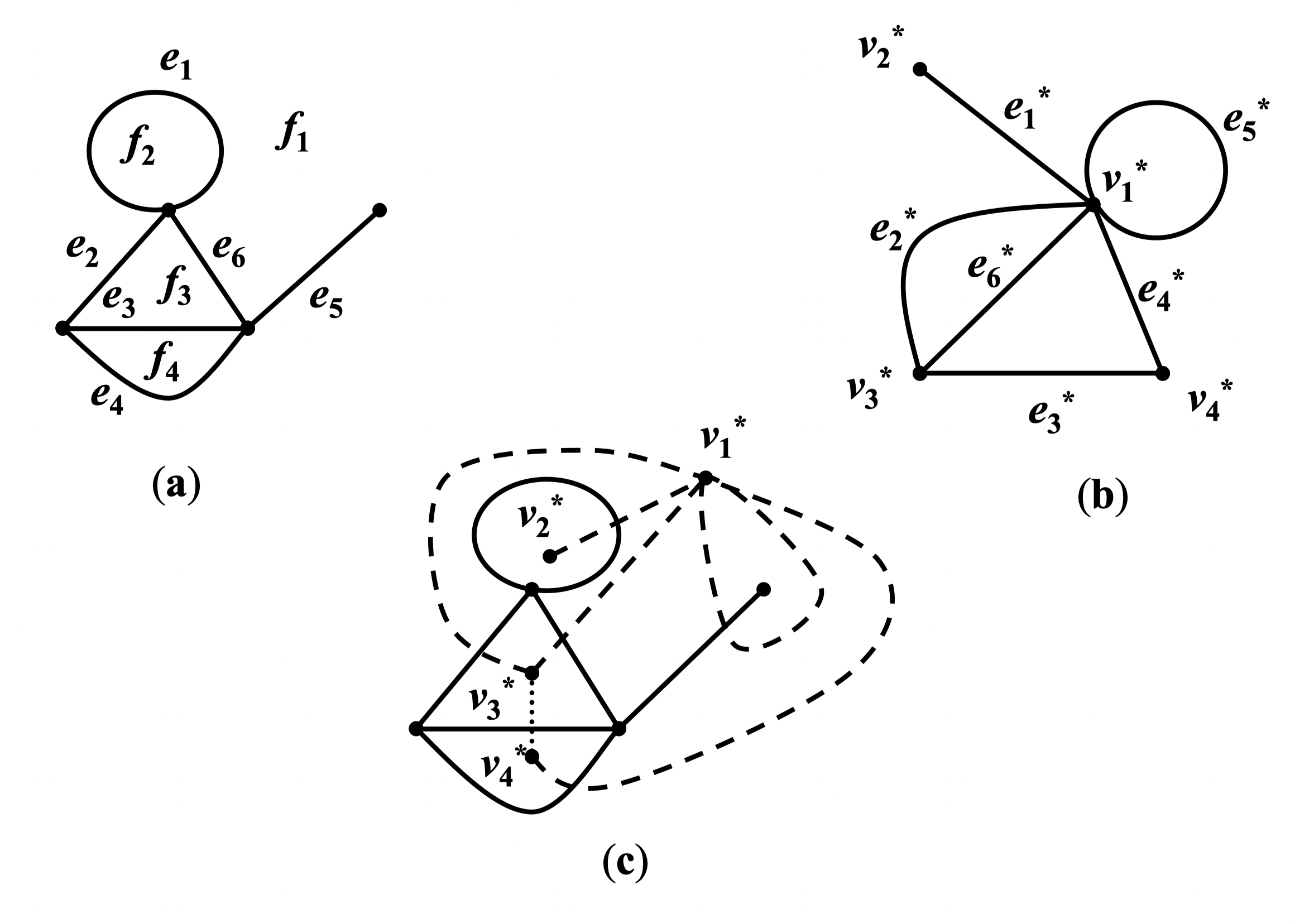
定理 85:平面图 的对偶图 也是平面图,并且还有
- 的点数 = 的面数
- 的边数 = 的边数
- 的面数 = 的点数 ( 连通)
| 平面图 | |
|---|
| 点 | 面 |
| 边 | 边 |
| 环 | 割边 |
| 割边 | 环 |
| 回路 | 边割 |
| 边割 | 回路 |
定理 86:设 是平面图 的对偶图,则 必连通
 注:无论 是否连通, 总是连通的,因此 不一定等于
注:无论 是否连通, 总是连通的,因此 不一定等于
定理 87:假定 是平面图,则 当且仅当 是连通图
 注:同构的平面图可以有不同构的对偶图
注:同构的平面图可以有不同构的对偶图
例:下图中的两个图是同构的,但它们的对偶图却不同构
原因: 中有次数是 1 的面,而 没有次数是 1 的面
例:设至少具有两个连通分支的平面图 的点数、边数、面数分别为 ,求对偶图 的面数
解:根据对偶图的结论有:
又根据欧拉推论公式:
求得:
平面图的判定
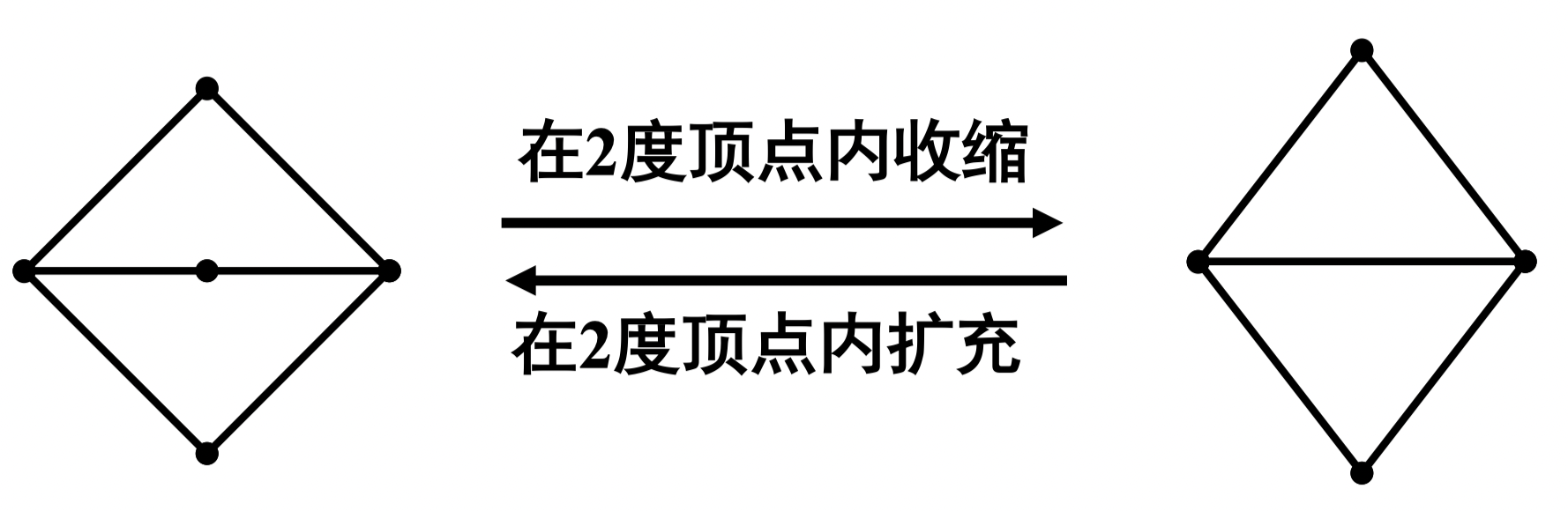
定义 95:在图 的边上插入一个新的 2 度顶点,使一条边分成两条边,则称将图 在 2 度顶点内扩充;去掉图 的一个 2 度顶点,使这个 2 度顶点关联的两条边合成一条边,则称将 在 2 度顶点内收缩
例:
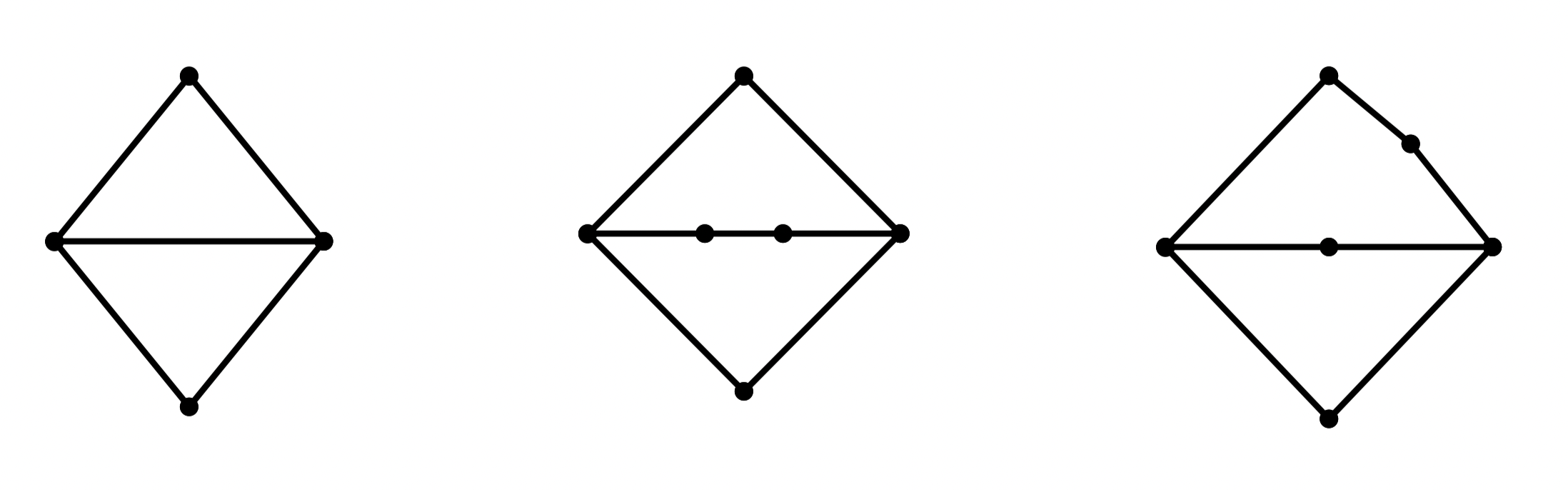
定义 96:两个图 和 ,如果 ,或者通过反复在 2 度顶点内扩充和收缩它们能变成同构的,则称 和 是同胚的,或 和 在 2 度顶点内是同构的
例:下面三个图是两两同胚的
 注:图的可平面性在同胚意义下不变
注:图的可平面性在同胚意义下不变
定理 88 (库拉托夫斯基定理):图 是可平面的当且仅当它不含与 或 同胚的子图
 注:库拉托夫斯基定理可以等价叙述为:「图 是非可平面的当且仅当它含有与 或 同胚的子图」
注:库拉托夫斯基定理可以等价叙述为:「图 是非可平面的当且仅当它含有与 或 同胚的子图」
例:证明下图给出的两个图 和 为不可平面图
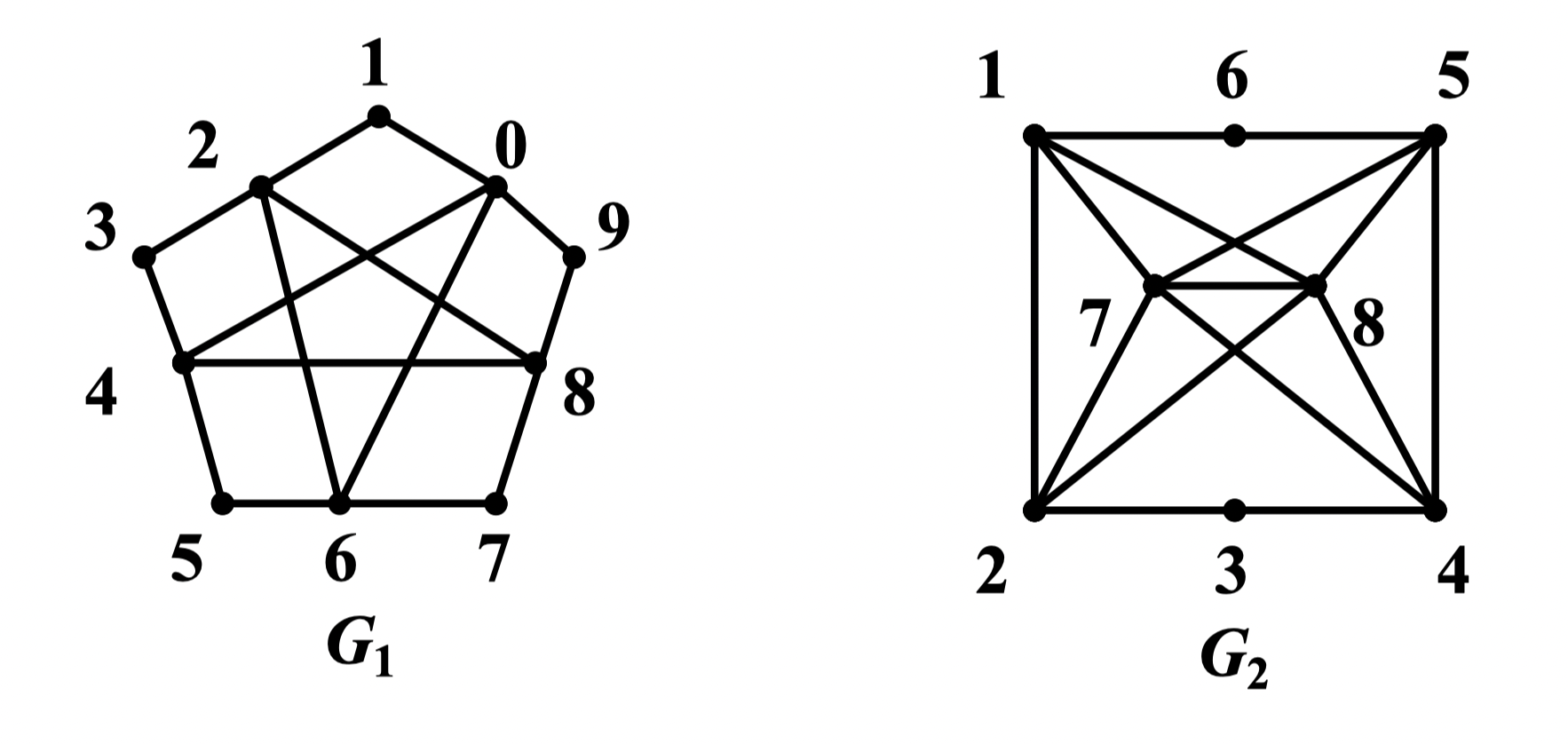
证明:对 ,在 2 度顶点内收缩点 得 ,即 本身同胚于 ,所以 是不可平面图
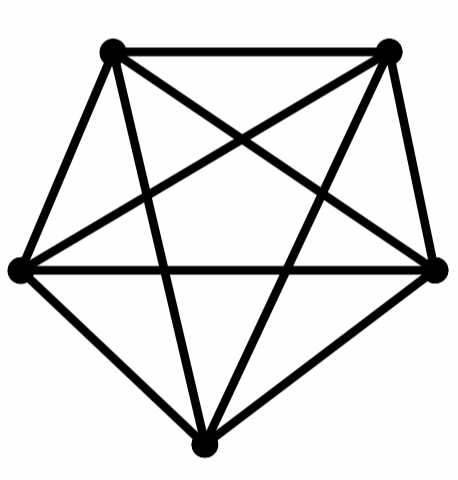
取 的一个子图:
收缩点 ,得 。所以 是不可平面图
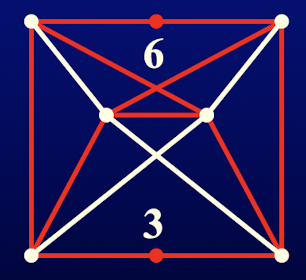
例:判断下图是否为可平面图
解:取红色的边导出的子图得到该图的一个子图:
上图显然和 同胚。因此,原图不是可平面图
思考:若图 与 同胚,则至少从 中删去 1 条边才可能使其成为可平面图
定义 97:给定图 ,去掉 中的环 (若有的话),将 中的重边 (若有的话) 用单边代替,称这样所得的图为 的基础简单图
定理 89:
- 图 是可平面图当且仅当其基础简单图是可平面图
- 图 是可平面图当且仅当它的每个块是可平面图
定义 98:设 是简单图 的一条边。去掉该边,重合其端点,再删去由此产生的环和重边。这一过程称为图 的初等收缩或收缩边 的运算,并记所得之图为
定义 99:一个图 可收缩到 ,是指 可从 通过一系列初等收缩而得到
例:图 , 均可收缩到
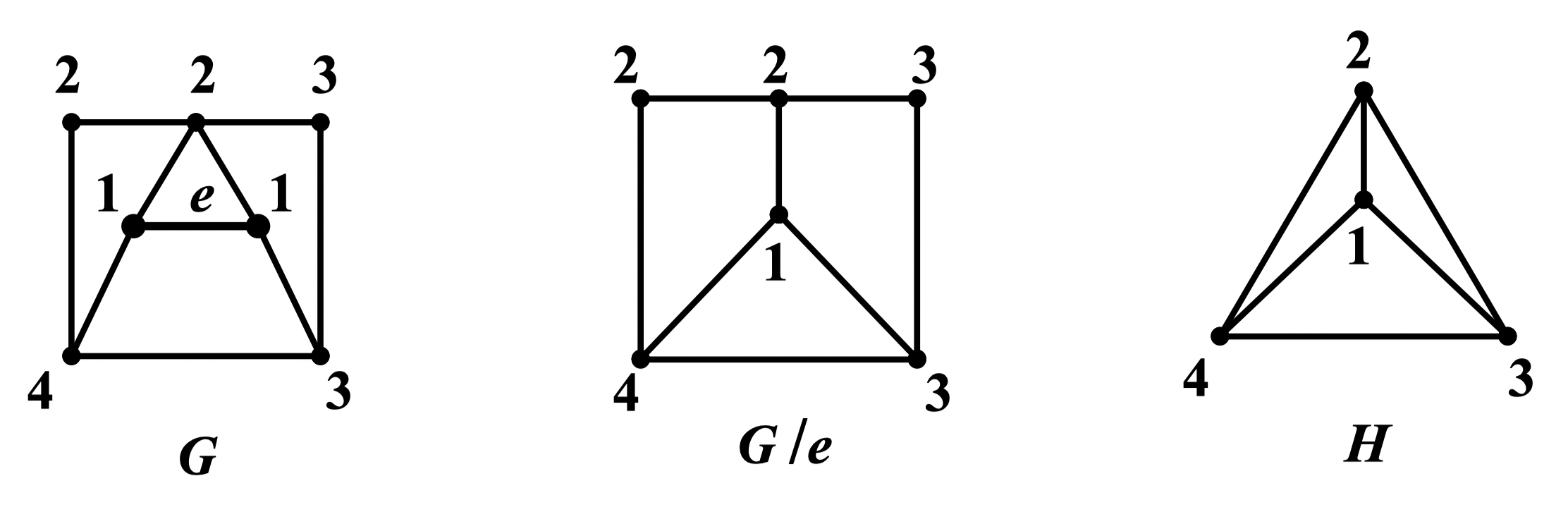
定理 90 (瓦格纳定理):简单图 是可平面图当且仅当它不含可收缩到 或 的子图
例:图 是不可平面图。因为由 通过收缩边 可得到图
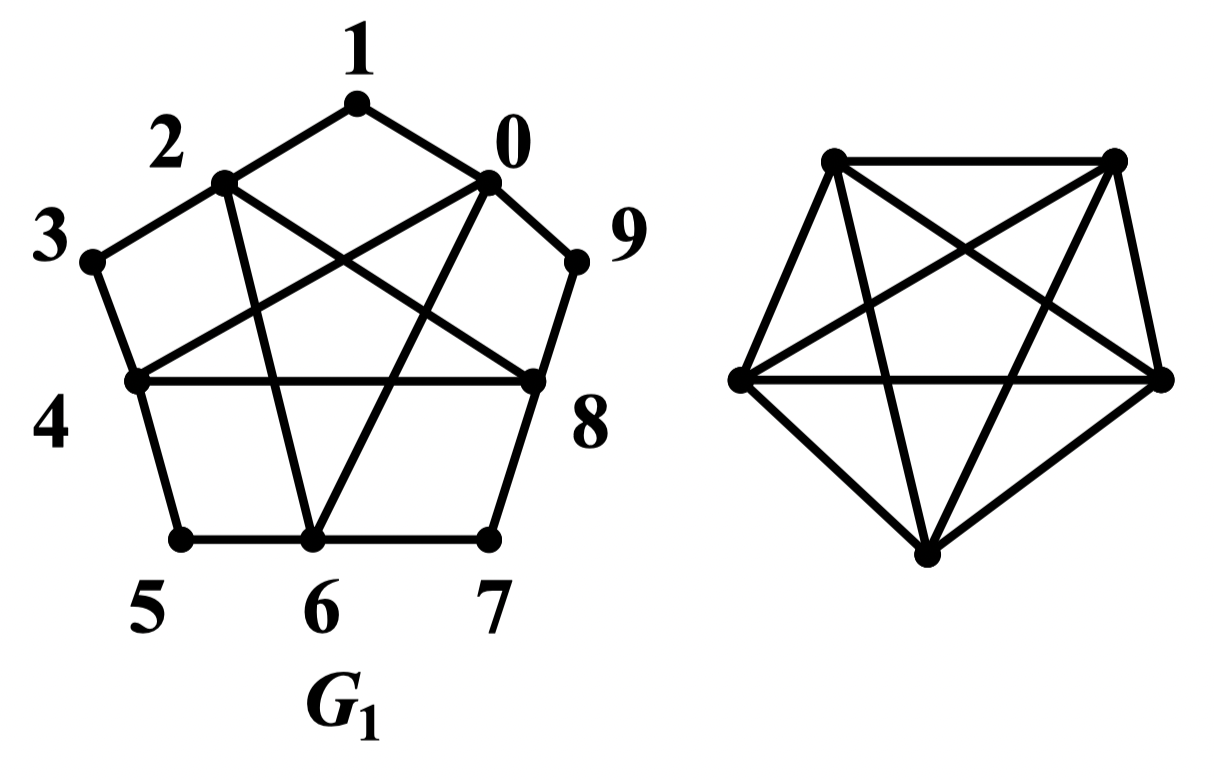
例:彼得森图通过收缩图中「红边」而得到图 ,故彼得森图是不可平面图
定理 91:至少有 9 个点的简单可平面图的补图是不可平面的,而 9 是这种数目中最小的一个
例:找出一个 8 个顶点的可平面图,使其补图也是可平面的
例:设 是一个 阶简单图且 ,则 与 的补图中至少有一个是非可平面图
解:
例:设 是一个具有 个点, 条边的图,。证明:若 和 同胚,则
证明:
涉及平面性的不变量简介
定义 100:若通过加上 个环柄可将图 嵌入球面,则 得最小值称为 的亏格,记为
例:
- 若 是可平面图,则
- 同胚的图是亏格相等
定理 92:对一个亏格为 ,有 个顶点, 条边和 个面的多面体,有
推论:设 是一个有 个点, 条边,亏格为 的连通图,则:
- 若 无三角形,则
- 若 每个面是三角形,则
- 若 每个面是四边形,则
定理 93:设 是正整数,则
定理 94:设 是正整数,则
定义 101:若图 的 个可平面子图的并等于 ,则称 的最小值为 的厚度,记为
 注: 是可平面图当且仅当
注: 是可平面图当且仅当
定理 95:对任意的具有 个点, 条边的简单图,有
定理 96:若 或 ,则
定理 97:设 是正整数,则
定义 102:将 画在平面上时相交的边对的最少数目称为 的叉数,记为
 注: 是可平面图当且仅当
注: 是可平面图当且仅当
定理 98:设 是正整数,则
定义 103:图 中边不重的不可平面子图的最多数目称为 的糙度,记为
定理 99:完全图的糙度由下式给出
是面数 平面性算法
定义 104:设 是图 的一个子图,在 上定义关系「」如下: 当且仅当存在一条途径 ,使得 (1) 的第一条边与最后一条边分别是 与 并且 (2) 的内部顶点与 不相交
易证关系 具有自反应,对称性和传递性,从而是 上的一个等价关系
此等价关系的等价类导出的 的子图称为 -片段。片段与 的公共顶点称为附着顶点
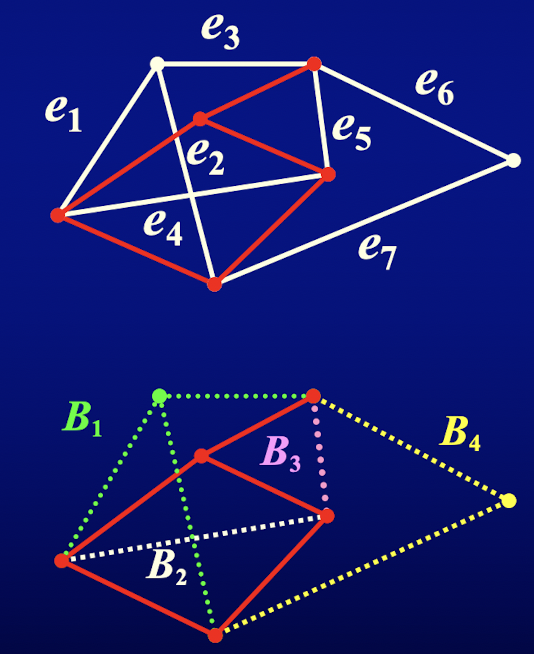
由片段的定义可直接推出:
- 若 是 -片段,则 是连通图
- 的任何两个顶点都有和 的内部不相交的路相连接
- 不计 的顶点,任意两 -片段没有公共顶点
例:在下图中取其子图,如实线所示。其余不同种类的线段表示该子图的四个不同的片段:
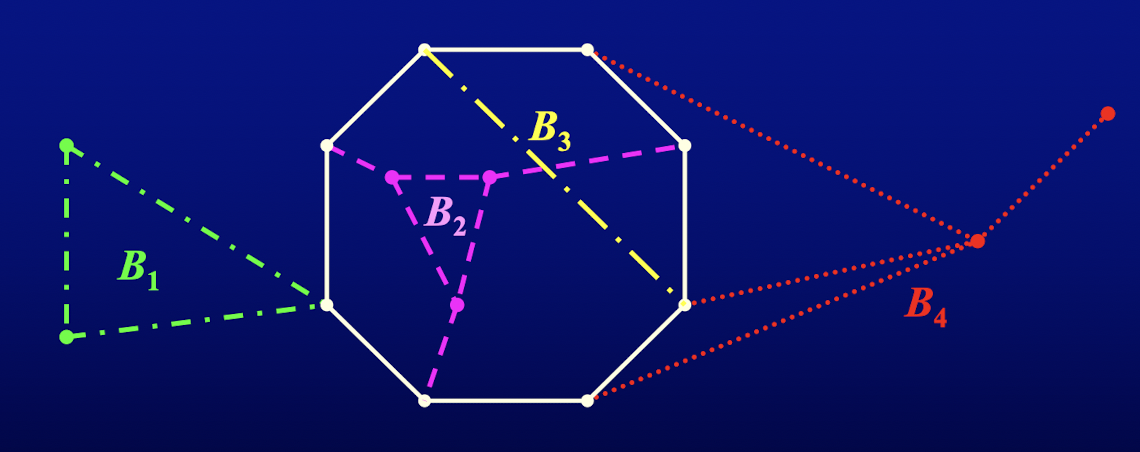
定义 105:设 是图 的一个圈,图 的两个 -片段 和 是冲突的,如果
- 和 在 上有三个公共的附着顶点;或
- 在 上存在四个顺序排列的顶点 使得 是 的附着顶点并且 是 的附着顶点
例:
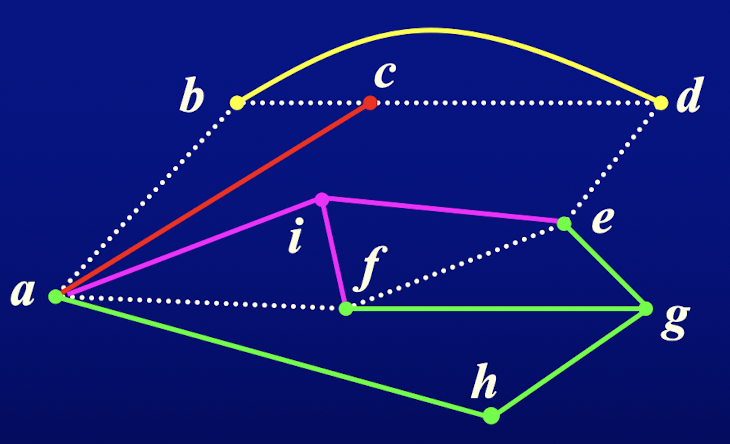
 注:冲突的两个片段无法同时平面嵌入到同一个面中
注:冲突的两个片段无法同时平面嵌入到同一个面中
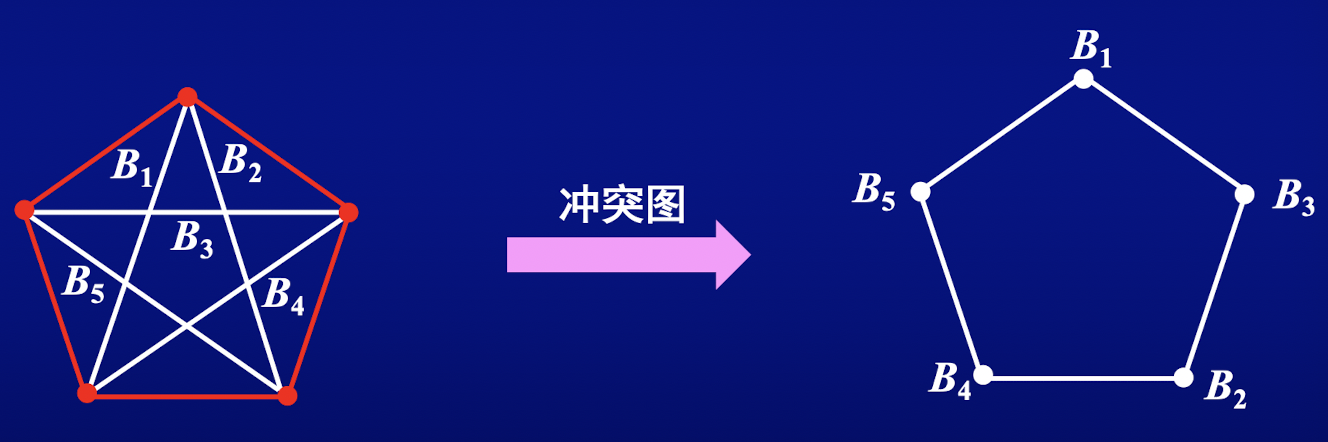
定义 106:设 是图 的一个圈,以图 的 -片段为顶点,顶点间连一条边当且仅当对应的 -片段是冲突的,把这样得到的图称为 的冲突图
例:画出 的哈密尔顿圈的冲突图
定理 100:图 是可平面的当且仅当对 的每个圈 ,其冲突图是二部图
证明:
定义 107:设 是图 的一个可平面子图, 是 的一个平面嵌入。假定 是子图 的任一片段,若 对 的所有附着顶点都位于 中某个面 的边界上,则称 在 的面 中是可画入的,否则,称为不可画入的。令 是的面且在中可画入
例:假定 如实线所示,则片段 在外部面上是可画入的,而 对面 和 均为不可画入的,且
平面性算法
设 是至少有三个顶点的简单块,取 的任意一个圈 ,求出 的一个平面嵌入。假设 已确定,下面确定
- 若 ,则停 (返回 可平面);否则,确定 的所有片段
- 对每个片段 ,求集合
- 若存在片段 ,使 ,则停 (返回 不可平面);否则,在 的所有片段中确定一个使 最小的片段 ,并取
- 在片段 上取一条连接 上两个附着点的路 ,把 画在 的面 内,置
- 令 ,转第 1 步
例:用平面性算法判断下图 的平面性
解:
例:证明:每个 5 连通的简单图可平面图至少有 12 个顶点
证明:设 是一个满足条件的 5 连通图,则
由握手定理知:
又因为 是简单可平面图,故
因此,。从而,
例:若 是一个连通平面图且满足 ,则 至少有一个面使得
证明:若不然,则
由欧拉公式得:
因此,
另一方面,由 知:
这样导出矛盾!!
例:若平面图 是自对偶的 (即 ),则
证明:假设 的阶数为 ,则
又因为 ,所以 ,从而
易知,自对偶图一定是连通图。因此,对于图 ,欧拉公式成立
故:。因此,
例:证明:不存在有 5 个面,且任意两个面之间至少存在一条公共边的平面图
证明:假设 是满足条件的图,则 恰有 5 个点且 中任意两点之间均有边存在,故
因此, 不是平面图,矛盾!!
例:设 是平面上的一个任意两点间的距离至少为 1 的点集。证明: 中最多有 个点对,它们之间的距离恰好为 1
证明:
第七章 图的着色
图的边着色
排课表问题:设有 位教师, 个班级,其中教师 要给班级 上 节课。求如何在最少节次排完所有课
图论模型:令 , 与 间连 条边,得偶图 。于是,问题转化为如何在 中将边集 划分为互不相交的 个匹配,且使得 最小
如果每个匹配中的边用同一种颜色着色,不同匹配中的边不同颜色,则问题转化为在 中给每条边着色,相邻边着不同色,至少需要的颜色数
定义 108:设 是图,对 的边进行着色,若相邻边着不同颜色,则称对 进行正常边着色;如果能用 种颜色对图 进行正常边着色,称 是 边可着色的
定义 109:设 是图,对 进行正常边着色需要的最少颜色数称为 的边色数,记为:
例:一个正常边着色:
定义 110:在对 正常边着色时,着相同颜色的边集称为该正常边着色的一个色组
偶图的边色数
显然,在任何正常边着色中,与任一顶点相关联的各边必须着不同色,由此推知:对无环图
例:给出 的一个正常 边着色,由此证明:
证明:
例:用最少的颜色对 正常边着色
解:
定义 111:设 是 的一种正常边着色,若点 关联的边的着色没有用到色 ,则称点 缺 色
定理 101 (König):若图 是偶图,则
证明:
一般简单图的边色数
引理:设 是简单图, 与 是 中两个不相邻的顶点, 是 的一个正常 边着色。若对该着色, 以及与 相邻的点均至少缺少一种颜色,则 也是 边可着色的
定理 102 (Vizing):若图 是简单图,则 或
证明:
 注:根据维津定理,简单图可以按边色数分成两类图,一是边色数等于 的简单图,二是边色数等于 的图
注:根据维津定理,简单图可以按边色数分成两类图,一是边色数等于 的简单图,二是边色数等于 的图
几类特殊简单图的边色数
定理 103:若 是非空简单图。若 中恰有一个度为 的点,或 中恰有两个度为 的点并且这两个点相邻,则
证明:
定理 104:若图 是 阶简单图,若 且边数 ,则
证明:
例:试确定图中所给出的 4 个 5 阶图的边色数
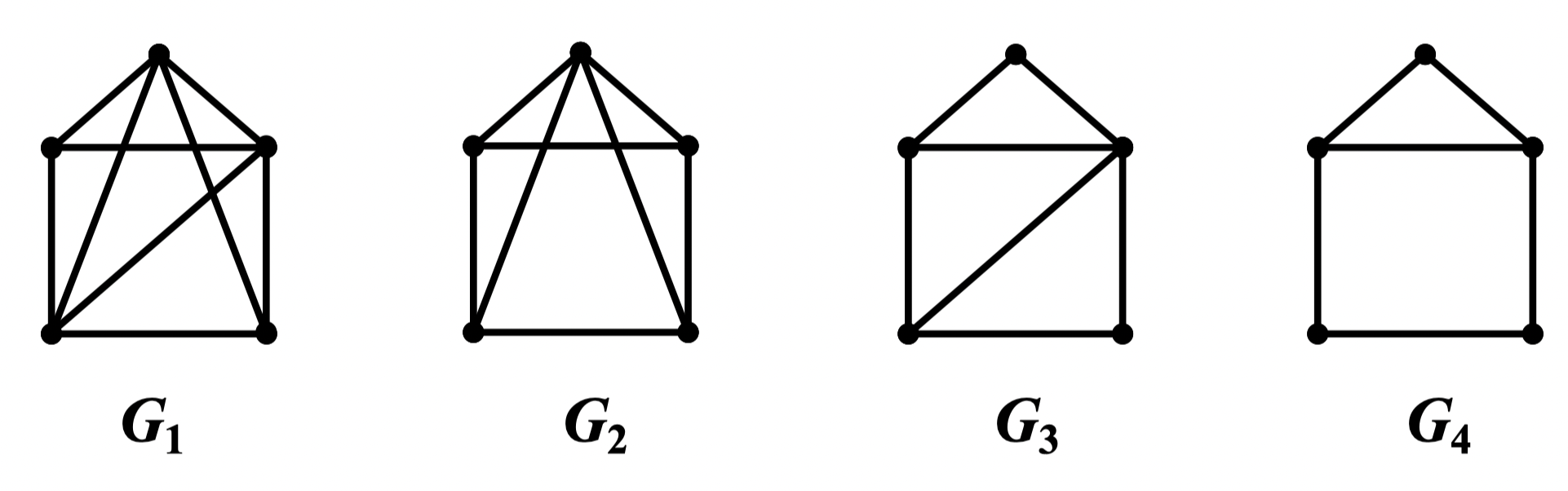
解:对 ,点数 ,边数 ,,满足 ,从而
对 ,它们都不满足 ,但均满足定理,故
引理:设 是奇阶 正则简单图。若 ,则
证明:
例:设 。求 和 ,其中 为 圈
解:因 是 2 正则简单图, 是 正则简单图,所以,,
例:求彼得森图的边色数
解:彼得森图不能进行 1 因子分解,所以,
所以,彼得森图的边色数为 4
定理 105:设无环图 的最大重数为 ,则
例:下图是一个边色数达到 的图,其中
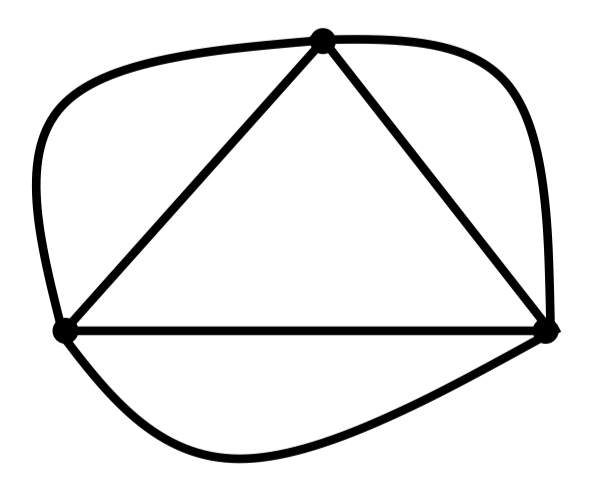
边着色的应用
排课表问题:
比赛安排问题:
顶点着色
定义 112:设 的一个图,对 的每个顶点着色,使得相邻顶点着不同颜色,称为对 的正常顶点着色;如果用 种颜色可以对 进行正常点着色,称 是 可着色的
定义 113:设图 正常顶点着色需要的最少颜色数,称为图 的点色数,简称色数,图 的色数用 表示
例:证明右图的色数是 4
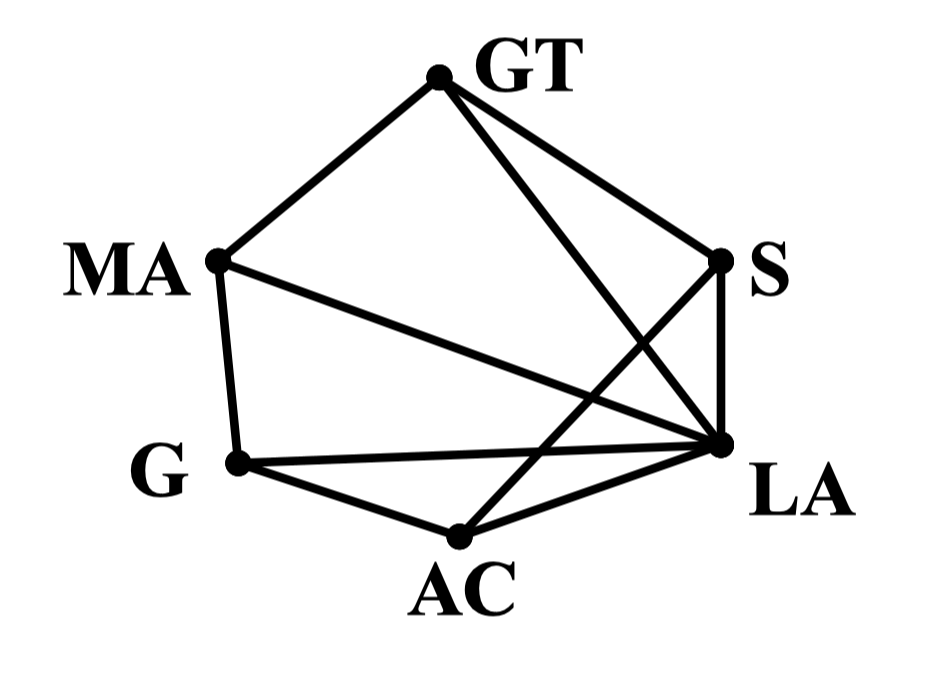
 注:对图的正常顶点着色,带来的是图的顶点集合的一种划分方式。着同一种颜色的顶点集合称为一个色组,它们彼此互不相邻,所有又称为点独立集
注:对图的正常顶点着色,带来的是图的顶点集合的一种划分方式。着同一种颜色的顶点集合称为一个色组,它们彼此互不相邻,所有又称为点独立集
定义 114:色数为 的图称为 色数
关于色数的若干结论
定理 106:对任意的无环图 ,均有
证明:
着色算法
给定图 ,设 ,着色函数为 ,色集
令
若 ,则停;否则令 并且与相邻
设 为 中的最小正整数,令
令 ,转 (2)
例:试用着色算法给下图顶点着色
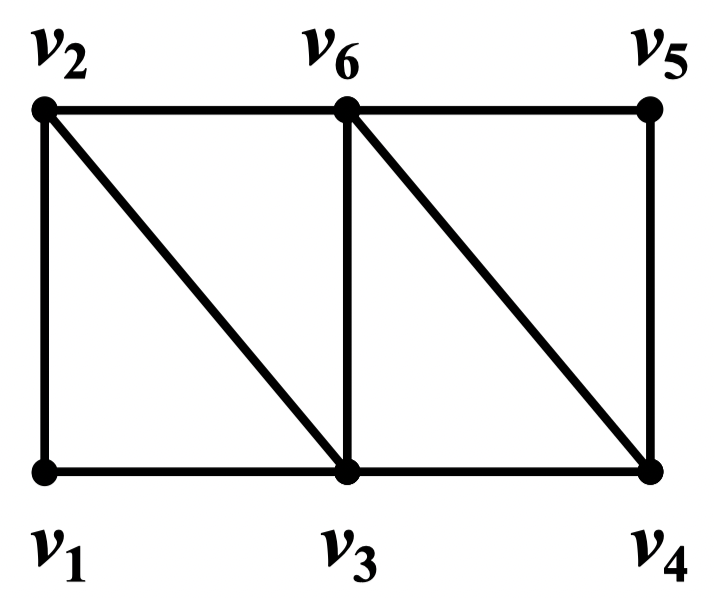
解:设 为着色函数,色集 ,着色过程如下:
定理 107 (Brooks):设 是简单连通图。假定 既不是完全图又不是奇圈,则
给定非空 (至少含一条边) 简单图 ,定义 。其中, 为 中与 相邻的点构成的集合。
如果令:,中存在点,满足,那么:
不混淆时, 也记为 。显然有 。 称为图 的次大度
例:对于图 ,
对于图 ,
定理 108:设 是非空简单图,则
 注:此定理是对 的一个改进!!!
注:此定理是对 的一个改进!!!
例:考察简单图
解:由布鲁克斯定理得:
根据次大度得:
引理:设 是非空简单图,若 中度数最大的点互不相邻,则
四色定理 && 五色定理
定理 109 (Heawood):对任意的简单平面图,均有
顶点着色的应用
课程安排问题:
交通灯的相位设置问题:
与色数有关的几类图
定理 110:设 是唯一 可着色图,,则
- 在 的任意一种 着色图中, 的任意两个色组的并导出的子图是连通的
 注意
注意
- 唯一 1 可着色图是空图
- 唯一 2 可着色图是连通的偶图
- 唯一 4 可着色可平面图都是极大可平面图
色多项式的概念
假定与记号
- 假定着色是正常的点着色
- 假定所给图是标号图,即图中若某特定点着不同色,则视为不同的着色法
- 用 表示图 的 着色数目
所谓着色的计数,就是给定标定图 和颜色数 ,求出正常顶点着色的方式数,并用 表示
可以证明: 是 的多项式,称为图 的色多项式
由 及 的定义,有
- 若 ,则 ;
- 若 为 阶空图,则
- 若图 含有 个孤立点,则 ,其中 是 去掉 个孤立点后所得的图
- 若图 有环或有重边,则去掉环并将重边用单边代替之后得图的 着色数目与原图一样
- 是具有 个点的树,则
递推计数法 (掌握一种即可)
记号 表示 中删去边 再重合 的端点后所得的图
定理 111:设 是简单图,则对 的任意边 ,有
证明:设 。 的所有 着色可分为两类
一类为 与 着不同色的 着色,此类着色相当于 的着色,其数目有 个
另一类为 与 着同色的 着色,此类着色相当于 的着色,其数目有 个
所以,
因此,
推论:设 是图 的一条边,并且 ,则
 注意
注意
- 当图的边数较少时,使用减边递推法
- 当图的边数较多时,使用加边递推法
例: 如图所示,分别求其色多项式
解:为了方便起见,递推的中间过程直接由图表示



 注:递推计数法的计算复杂度是指数型的
注:递推计数法的计算复杂度是指数型的
理想子图法 (必须掌握)
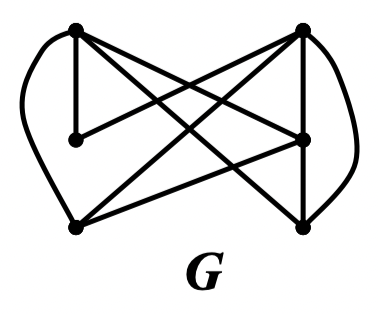
定义 115:设 是图 的生成子图。若 的每个分支均为完全图,则称 是 的一个理想子图。用 表示 的具有 个分支的理想子图的个数
例:求图 的全部理想子图
解:


定理 112:设 是具有 个点 条边的简单图,则有
- 若 ,则
定理 113:设 表示将简单图 的顶点集合 划分为 个不同色组的色划分个数,则:
 注:上述定理实际上给出了色多项式的求法:用 种颜色对简单图 正常着色,可以这样来计算着色方式数:
注:上述定理实际上给出了色多项式的求法:用 种颜色对简单图 正常着色,可以这样来计算着色方式数:
- 色组为 1 的方式数 + 色组为 2 的方式数 + + 色组为 的方式数
推论:对 阶简单图 ,有 ,其中
定义 116:设 的简单图,令 ,称多项式 为图 的伴随多项式
着色算法:先求出 的补图的伴随多项式,再将多项式中的 换成 便能得到简单图 的色多项式
例:求图 的色多项式
解: 的补图为:
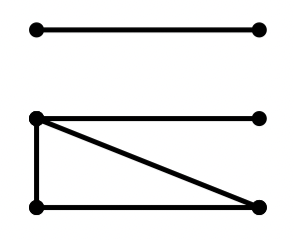
补图的伴随多项式为:
将 代入伴随多项式中得到 :
定理 114:若 有 个分支 ,且 的伴随多项式为 ,则:
 注:该定理说明,在求 的补图的伴随多项式时,可以分别求出它的每个分支的伴随多项式,然后将它们作乘积
注:该定理说明,在求 的补图的伴随多项式时,可以分别求出它的每个分支的伴随多项式,然后将它们作乘积
例:求图 的色多项式
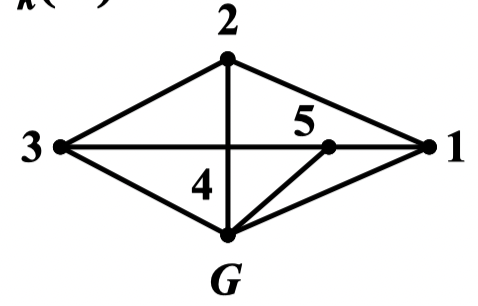
解:画出 的补图
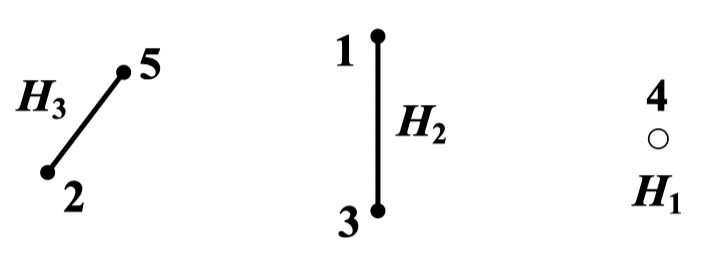
求出补图中各个分支的伴随多项式
求出补图的伴随多项式:
求出 的色多项式:
色多项式的性质
定理 115:对 阶简单图 , 是 的整系数 次多项式,首项为 ,常数项为零,并且各项系数的符号正负相间
证明:
 注意
注意
- 满足定理条件的多项式未必是一个图的色多项式,例如:多项式 便不是任何图的色多项式
- 同构的图有相同的色多项式,但其逆不真,例如下图所给的两个不同构的图 和 有相同的色多项式:
第八章 Ramsey 定理
独立集与覆盖
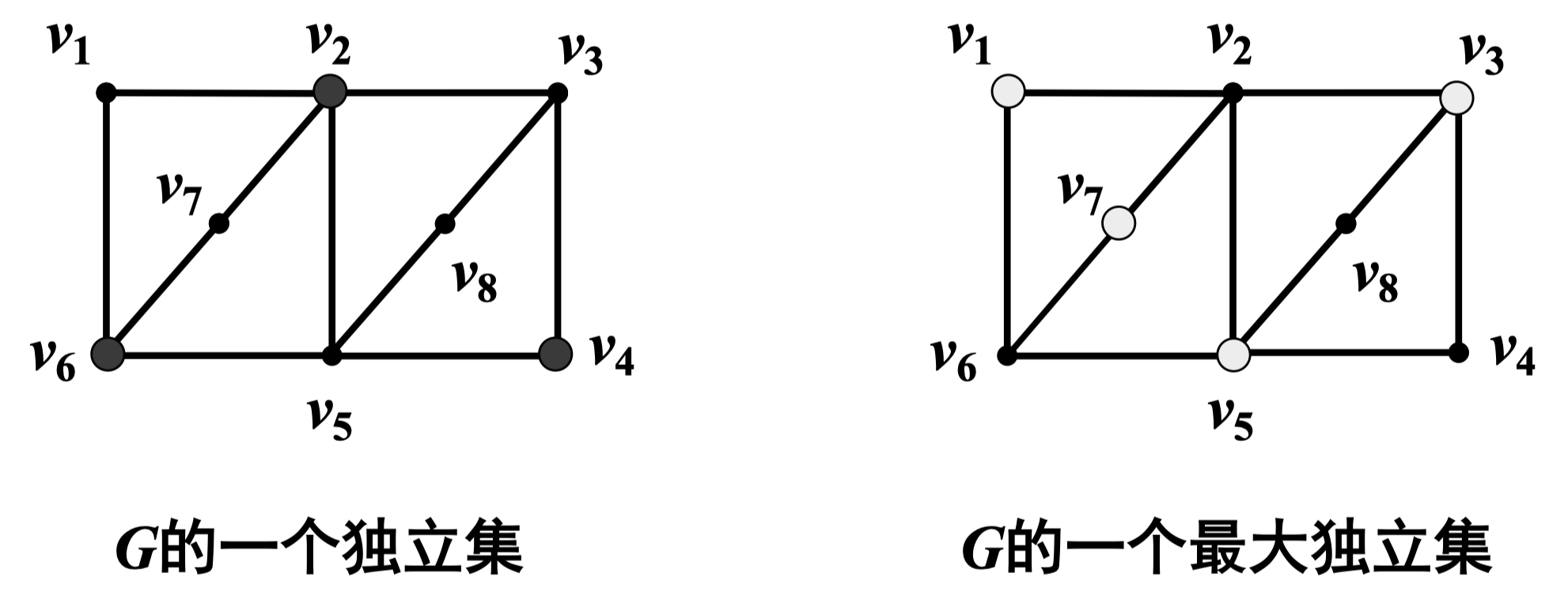
定义 117:设 ( 是一个图。 的一个顶点子集 称为 的一个独立集,如果 的顶点互不邻接。 的一个包含顶点数最多的独立集称为 的最大独立集。最大独立集包含的顶点数,称为 的点独立数,简称独立数,记为
例:
定义 118:设 ( 是一个图。 的一个顶点子集 称为 的一个覆盖,如果 中每条边至少有一个端点在 中
定义 119: 是一个包含顶点数最少的覆盖称为 的最小覆盖。 的最小覆盖包含的顶点数,称为 的点覆盖数,简称覆盖数,记为
例:
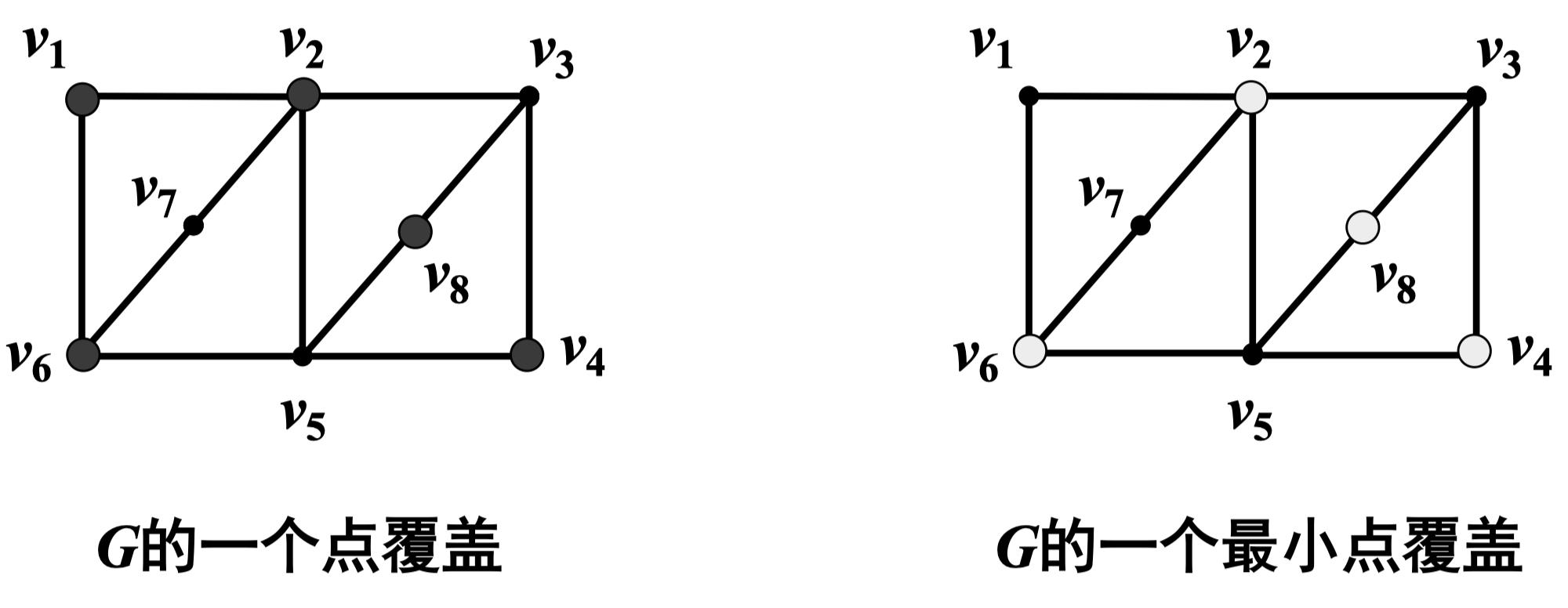
定理 116:给定图 且 ,则 是 的独立集当且仅当 是 的覆盖
证明:
定理 117 (Gallai):对任意的 阶图 ,有
边独立集与边覆盖
定义 120:设 ( 是一个图。 的一个边子集 称为 的一个边独立集,如果 的边互不相邻; 的一个包含边数最多的边独立集称为 的最大边独立集。最大独立集包含的边数,称为 的边独立数,记为
例:
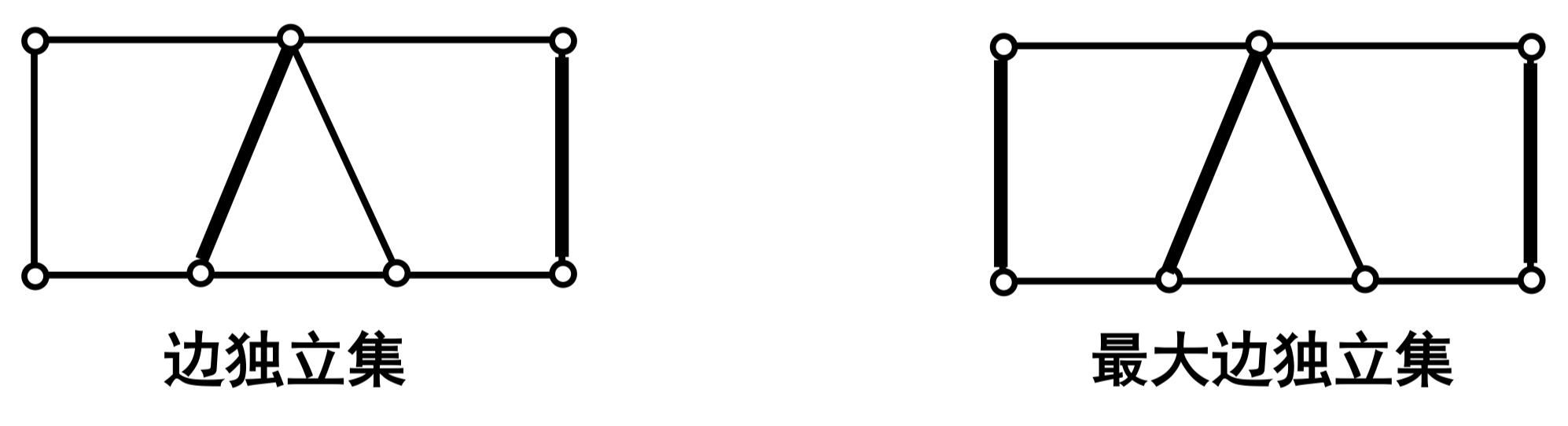
 注:一个边独立集实际上就是图的一个匹配,一个最大边独立集就是图的一个最大匹配
注:一个边独立集实际上就是图的一个匹配,一个最大边独立集就是图的一个最大匹配
定义 121:设 ( 是一个图。 的一个边子集 称为 的一个边覆盖,如果 中的每个顶点均是 中某条边的端点。 的一个包含边数最少的边覆盖称为 的最小边覆盖。最小边覆盖包含的边数,称为 的边覆盖数,记为
例:
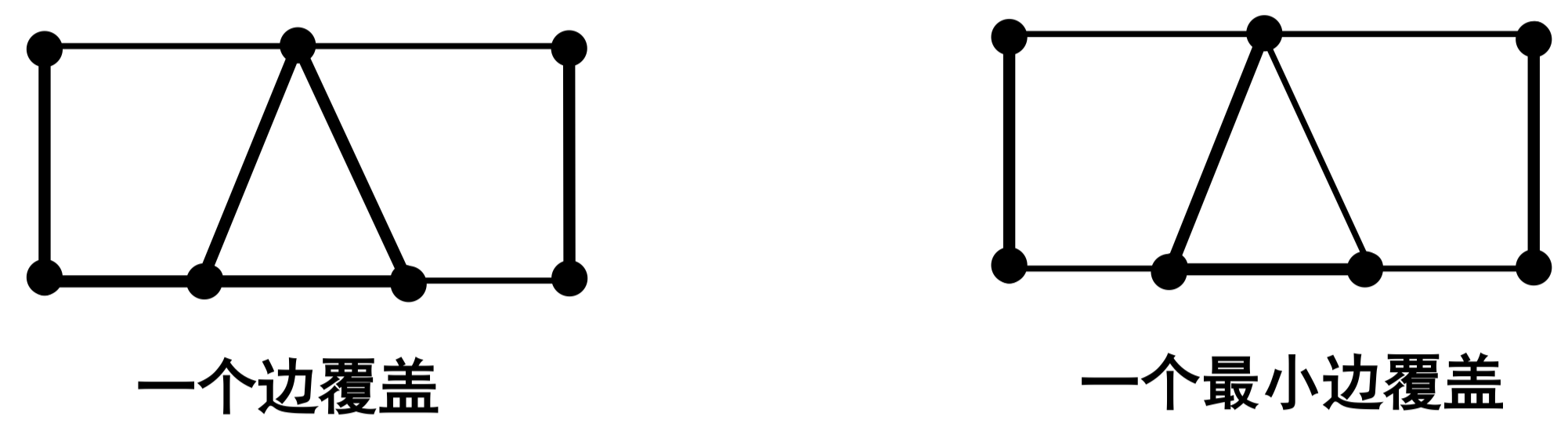
定理 118 (Gallai):对任意不含孤立点的 阶图 ,有
证明:
例:确定图 的
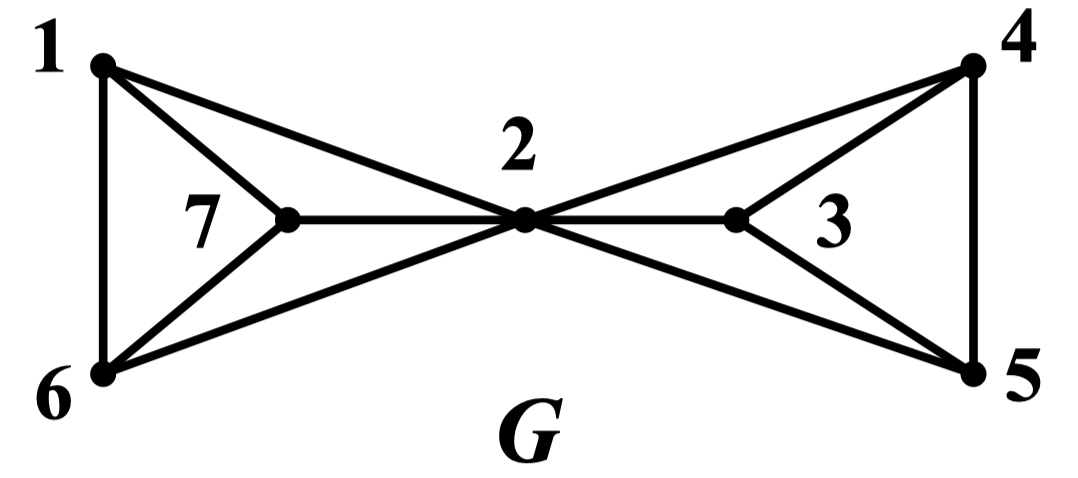
解:点 2 的左右两部分均是 ,所有可以推知 ,再由 Gallia 恒等式得:
又因为 的阶数为 7,所以 的最大边独立集包含的边数不会超过 3,即
在 中可找到边独立集:{16, 23, 45},所以
因此,,进而
定理 119: 设 是无孤立点的偶图,则 中最大独立集包含的顶点数等于最小边覆盖包含的边数
Ramsey 数 R(m, n)
定义 122:设 和 是两个正整数,令 是最小的正整数 ,使得任意的 阶图要么包含 个顶点的团,要么包含 个顶点的独立集。 称为 Ramsey 数
 注:由定义知
注:由定义知
例:求
解:
定理 120: 对于任意两个正整数 和 ,且 ,有 ,并且,如果 和 都是偶数,则上面不等式严格成立
例:已知 ,求 和
解:显然
显然
第九章 有向图
有向图
定义 123:一个有向图是一个称为点集的非空集合 和一个称为边集的集合 组成的二元组 。记为 ,简记为 ,其中 , 中每个元素均与 中一对有序点对相对应 (点对中的点允许相同)。 中的元素称为顶点或点, 中的元素称为有向边或弧,也简称边
定义 124:在有向图中,若边 和有序点对 相对应,则记 ,此时 称为 的始点或起点, 称为 的终点
定义 125:将有向图 的每条有向边 改为边 ,所得的无向图称为 的基础图
定义 126:给定无向图 ,将 中每条边 改为有向边边 或 ,所得的有向图称为 的定向图
 注:有向图的基础图唯一,而一个图的定向图并不唯一
注:有向图的基础图唯一,而一个图的定向图并不唯一
例:下图中,前两个为有向图,它们都是后一个的定向图
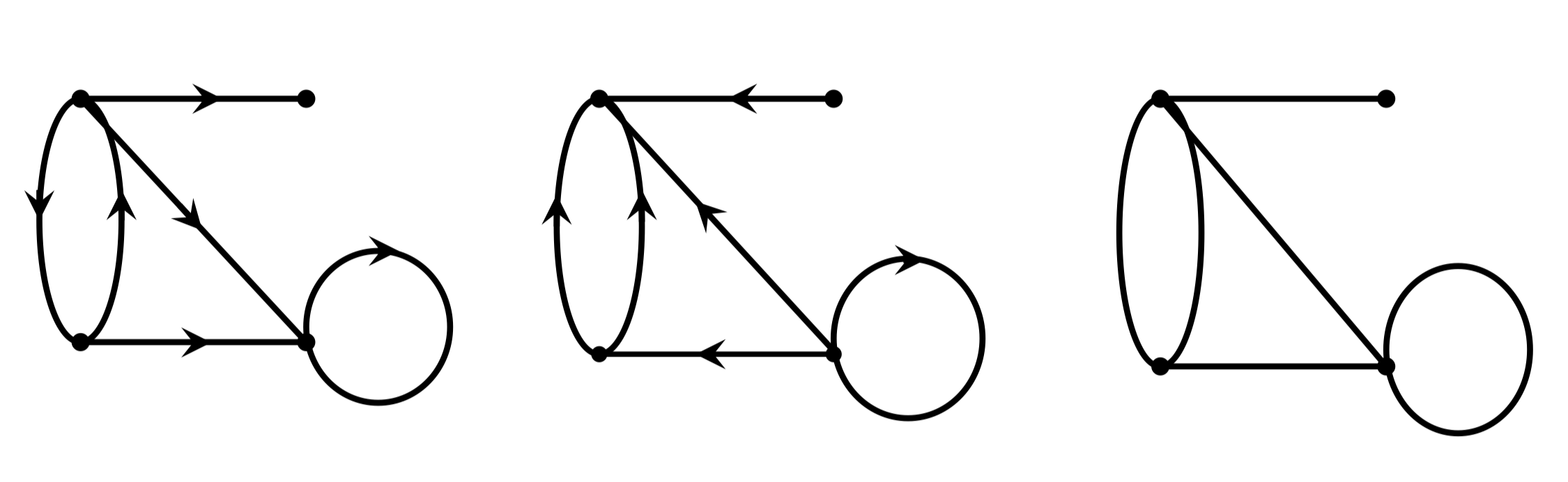
定义 127:设 是有向图 的一个顶点,称 中以 为始 (终) 点的边的数目为 的出 (入) 度,记为 ,称 的出度与入度之和为 的度,记为
例:对下图所示有向图,有
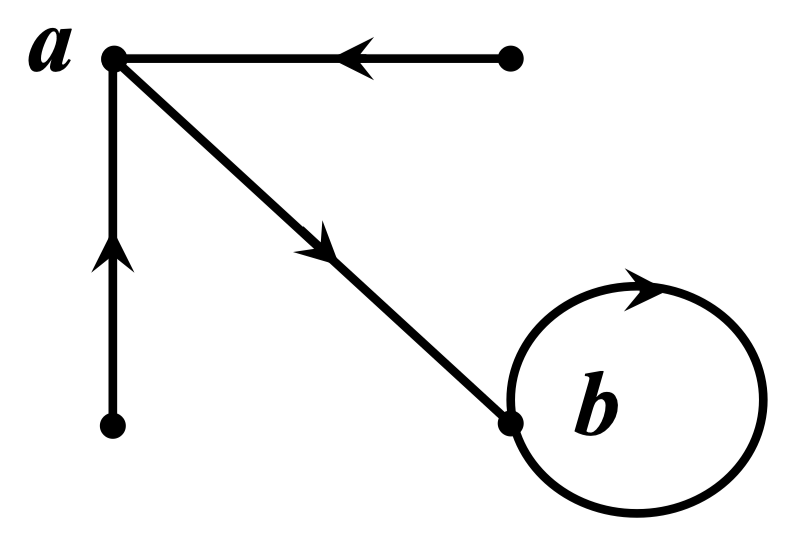
定理 121: 设 是一个有向图,则有
定义 128:设 条有向边的起点和终点均相同,则这 条边称为 重边, 称为这些边的重数。重数大于 1 的边也称为重边,重数等于 1 的边也称为单边。既无环又无重边的有向图称为简单有向图
定义 129:设 是一个标定有向图,其中设
- 称矩阵 为 的邻接矩阵,其中 是以 作为始点, 作为终点的边的数目,
- 若 无环,称矩阵 为 的关联矩阵,其中
是有向边的始点是有向边的终点其他 由定义可知,邻接矩阵 的所有元素之和等于边数;关联矩阵每一列恰有一个「1」和一个「-1」,第 行的 1 的个数等于 ,-1 的个数等于
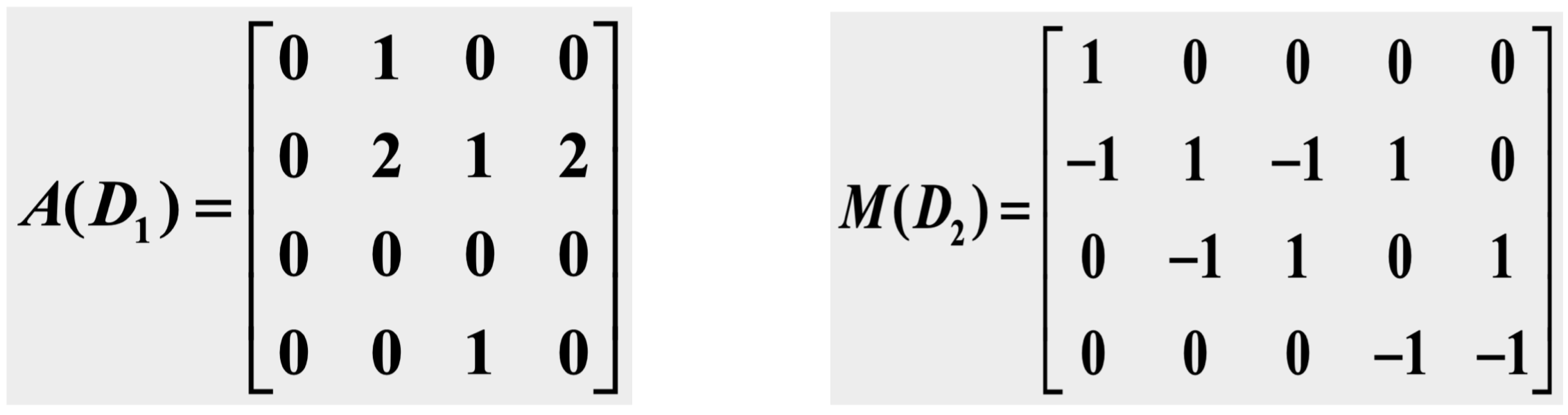
例:对下图所示的两个有向图 和 ,求 和
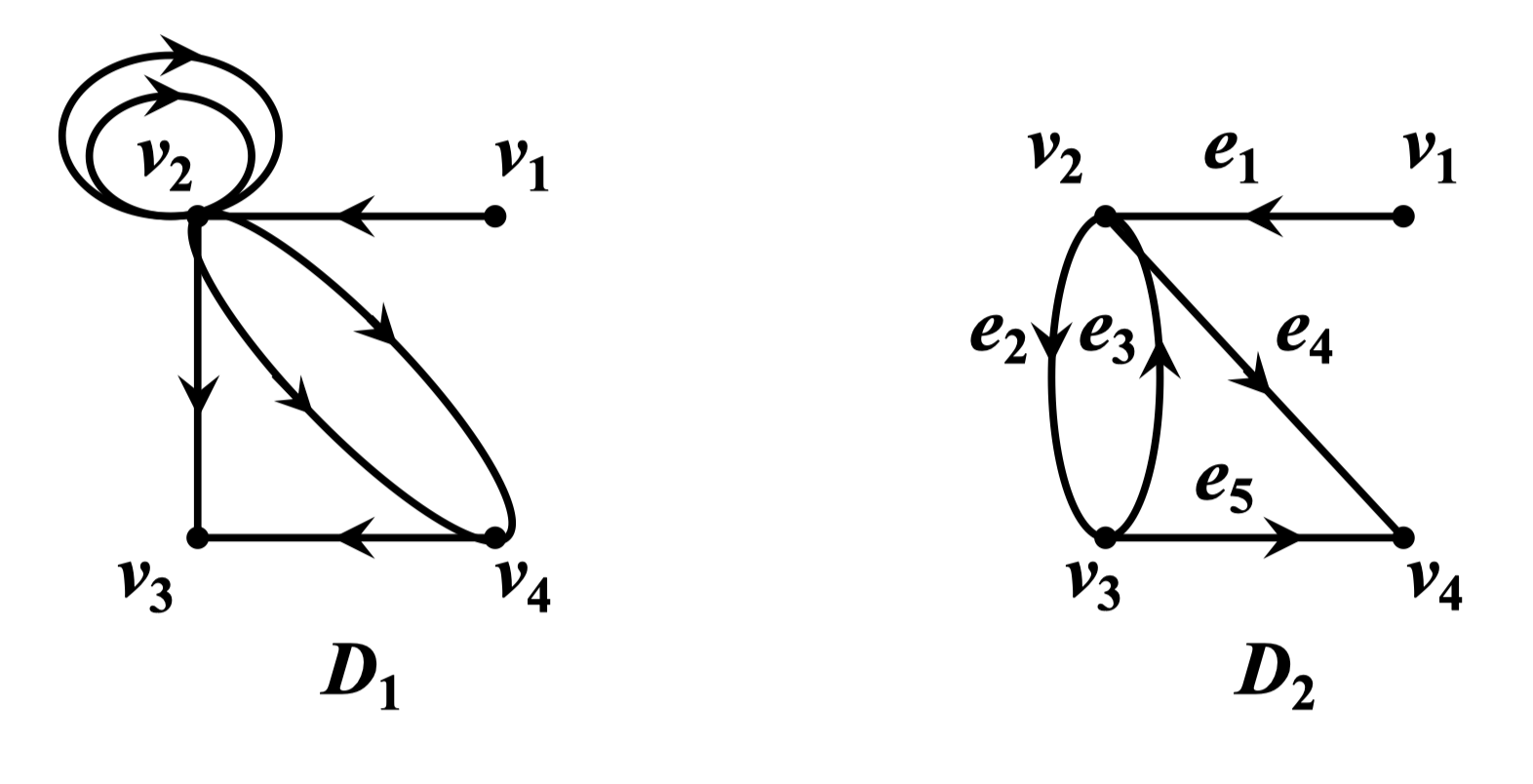
解:
有向图的连通性
定义 130:有向图 的一条有向途径是指一个有限非空点边交替序列 ,使得对 ,边 的始点为 ,终点为 。顶点 与 分别称为 的起点与终点, 称为 的长度
定义 131:边不相同的有向途径称为有向迹
 注:若 为标定有向图 的邻接矩阵,则 的第 行第 列的元素为 中从 到 的长为 的有向途径数目
注:若 为标定有向图 的邻接矩阵,则 的第 行第 列的元素为 中从 到 的长为 的有向途径数目
定义 132:设 和 为有向图 中的两个顶点,若 中存在有向 路,则称在 中 可达 ,记为 ,规定
定义 133:若 ,并且 ,则称 和 可互达,记为 。易知关系「」是 上的一个等价关系
定义 133:设 为一个有向图:
- 若对 , 与 可互达,则称 是强连通的
- 若对 ,或 ,或,则称 是单向连通的
- 若 的基础图是连通的,则称 是弱连通的,简称连通
 注:强连通一定单向连通,单向连通一定弱连通
注:强连通一定单向连通,单向连通一定弱连通
例:在下图中, 为弱连通; 为单向连通图; 为强连通图
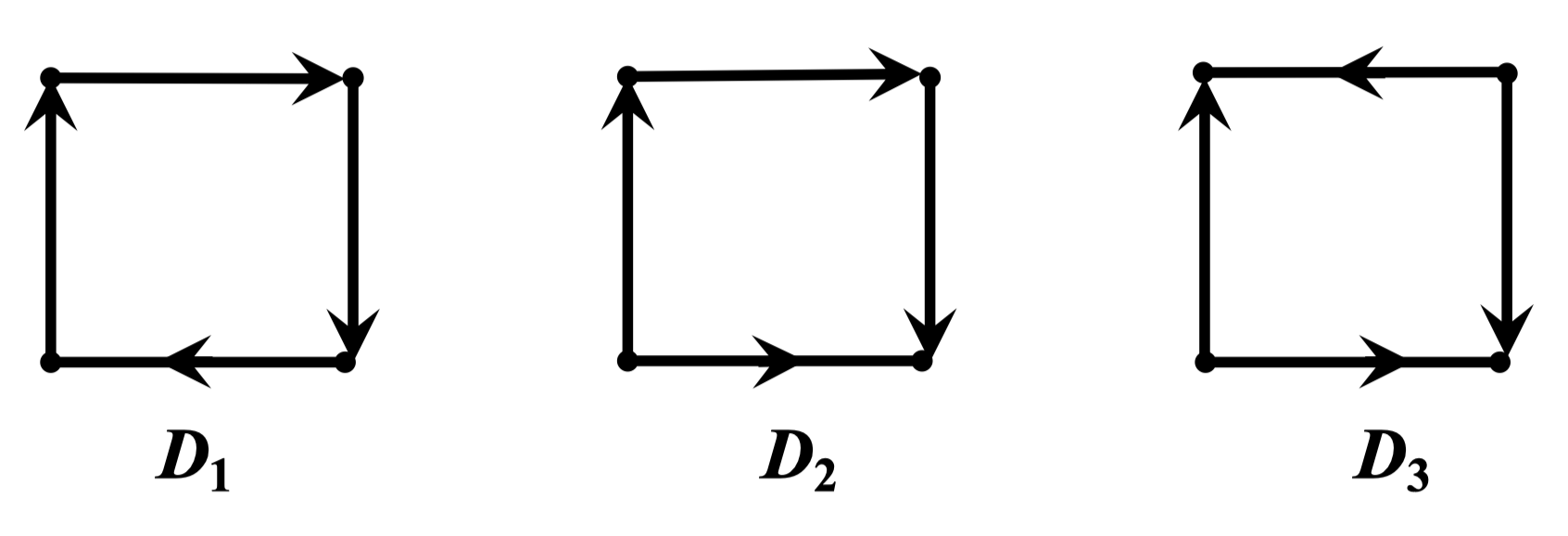
定理 122: 有向图 是强连通的当且仅当 中存在含有所有顶点的有向闭途径
例:判断下图是否为强连通图
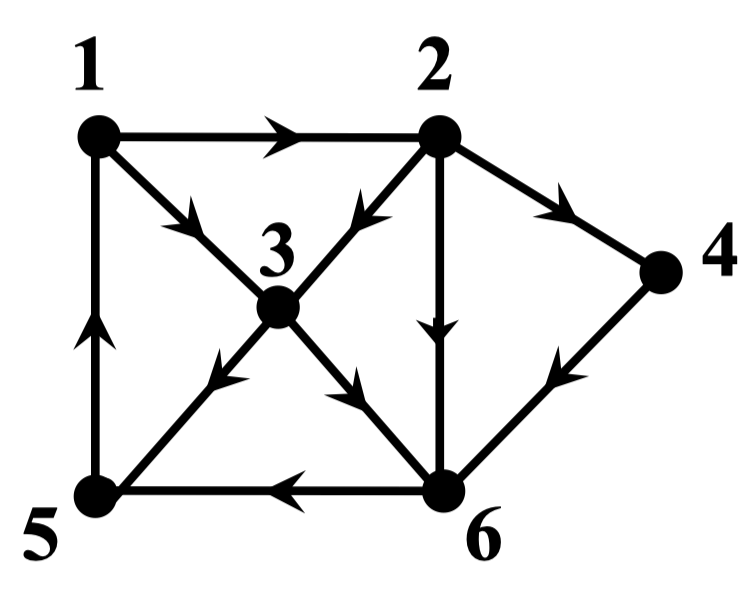
解:该图是强连通的。因为该图存在经过所有顶点的有向闭途径 124651351
定义 134:设 是有向图 的一个子图。如果 是强连通的 (单向连通的、弱连通的),且 中不存在真包含 的子图是强连通的 (单向连通的、弱连通的),则称 是 的一个强连通分支 (单向连通分支、弱连通分支)
例:求下图 的强连通分支、单向连通分支
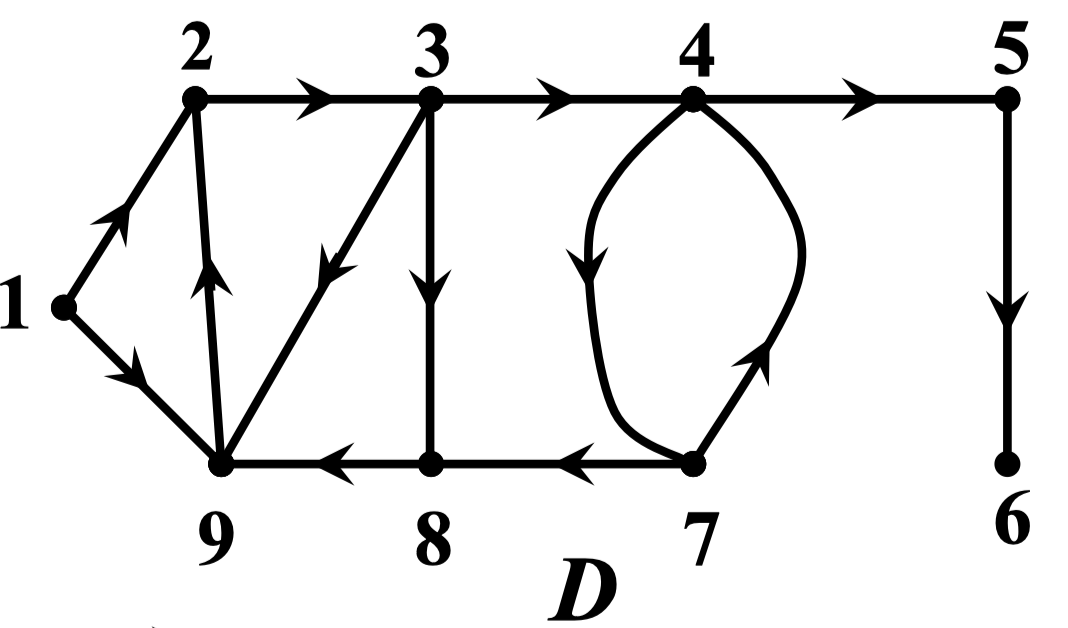
解: 的强连通分支:
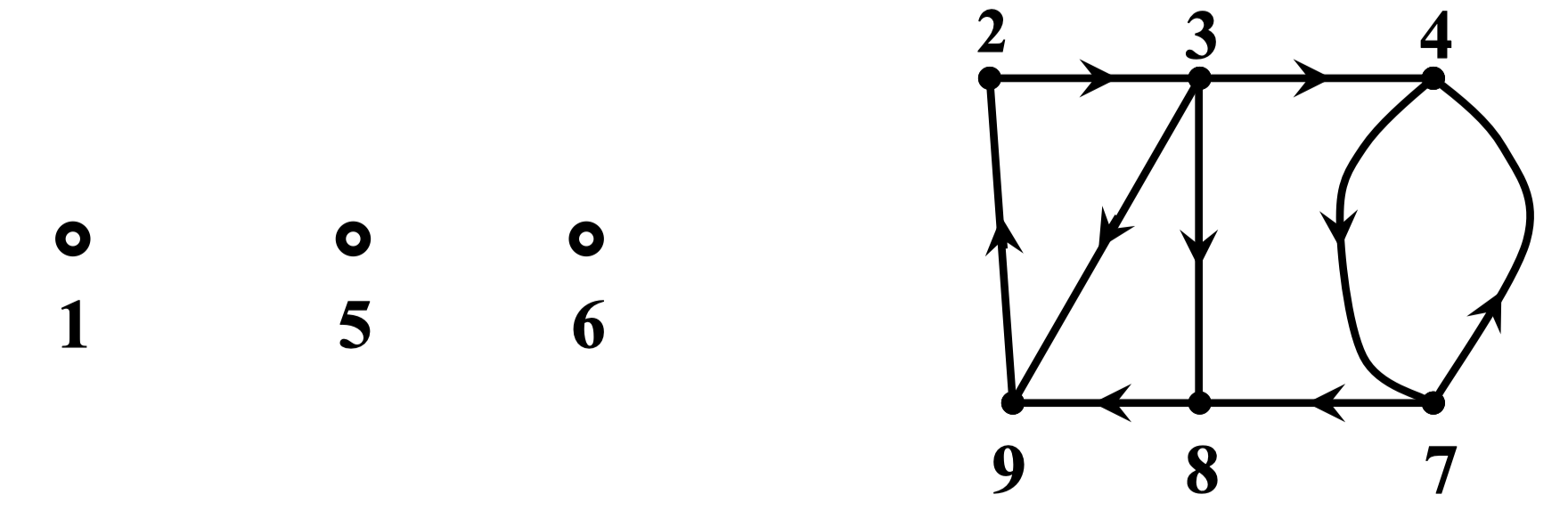
的单向连通分支就是 本身
定理 123: 有向图 的每个点位于且仅位于 的一个强 (弱) 连通分支中
 注:有向图 的某个顶点,可能会分属于 的若干个单向连通分支。因为单向连通关系不是等价关系
注:有向图 的某个顶点,可能会分属于 的若干个单向连通分支。因为单向连通关系不是等价关系
图的定向问题
定理 124: 若 是 2 边连通的,则 存在强连通定向图
有向树、跟树
定义 135:若有向图 的基础图是树,则称 为有向树
例:
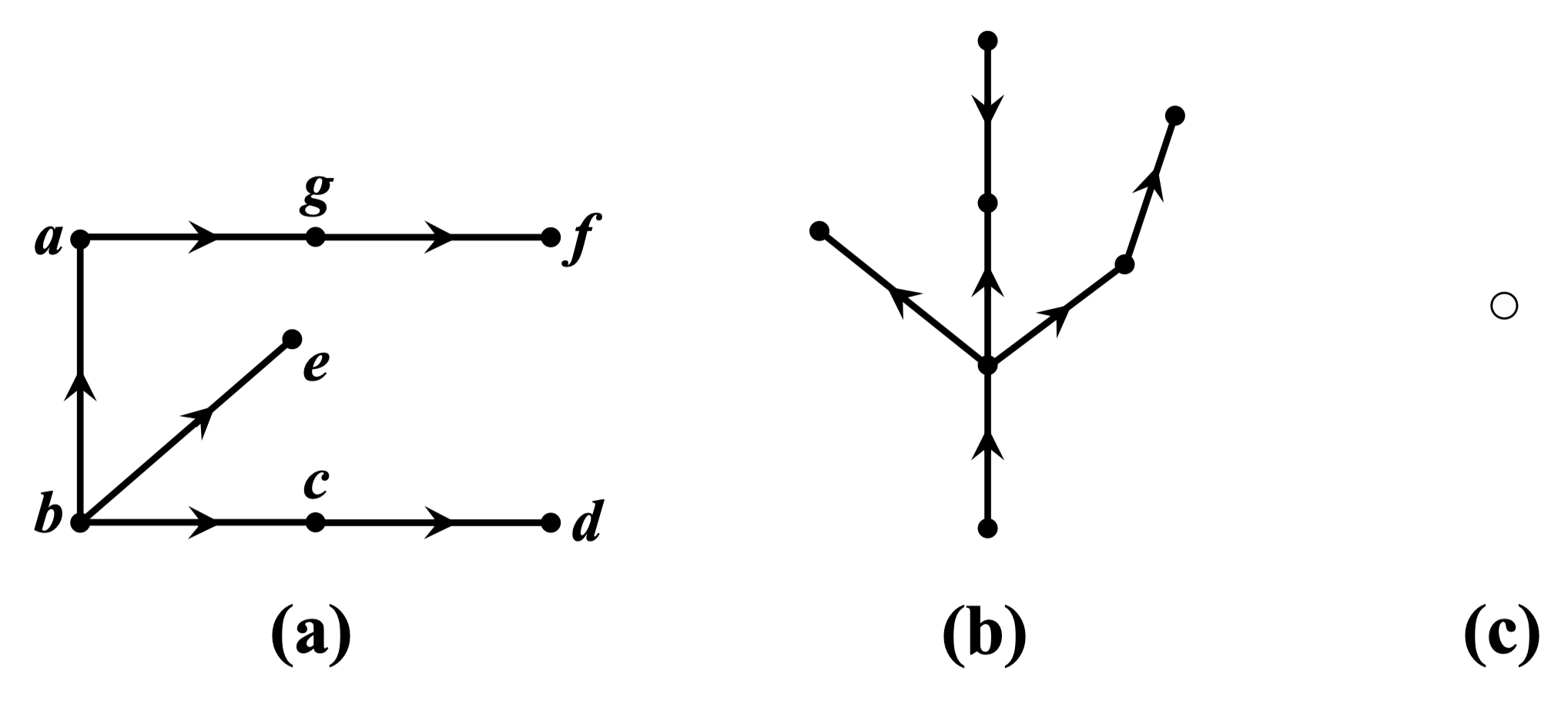
定义 136:恰有一个顶点的入度为 0,其余顶点的入度均为 1 的非平凡树称为根树。跟树中入度为 0 的顶点称为树根,出度为 0 的顶点称为树叶,其余点称为内点,内点和根统称为分支点
习惯是我们把根树的根画在最上方,并使有向边的方向均指向下方,对这种标准画法,有向边的箭头还可省去
例:
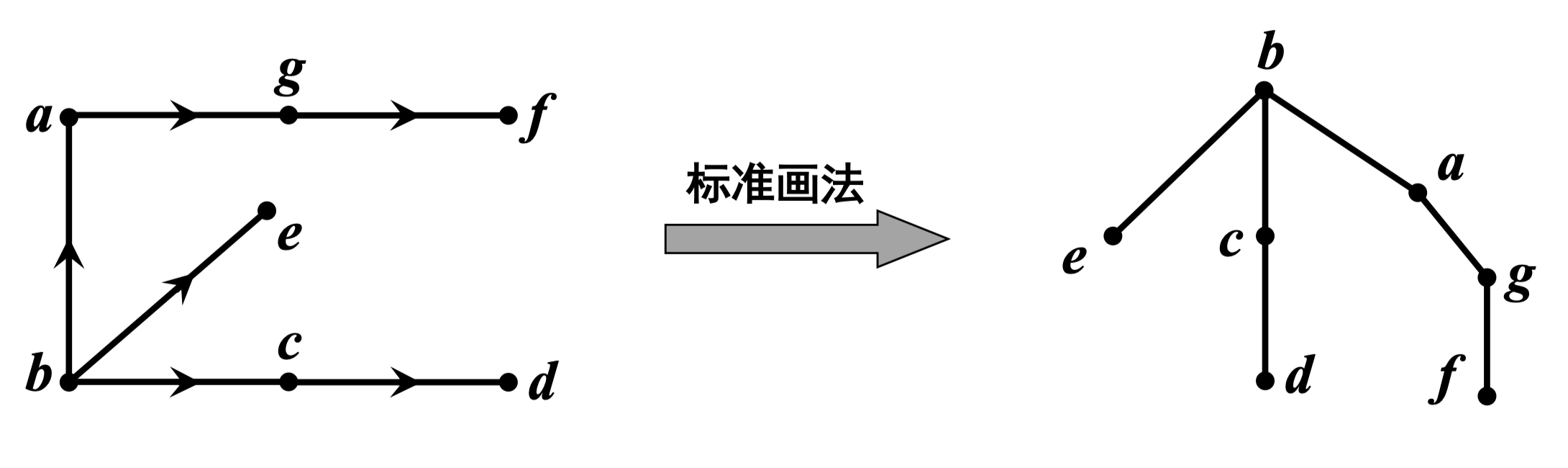
定义 137:根树中,从根到顶点 的距离称为 的层数,所有顶点的最大层数称为该树的高
定义 138:根树中,若点 ,则称 为 的祖先, 为 的后代;若 是根树中的有向边,则称 为 的父亲, 为 的儿子;若某 个顶点是同一个父亲的儿子,则这 个顶点称为兄弟
定义 139:设 为根树 的任一顶点,称 及其所有后代导出的子图为以 为根的子树
m 元树
定义 140:根树 中,若每个分支点至多有 个儿子,则称 为 m 元树;若每个分支点恰有 个儿子,则称 为 m 元完全树
例:
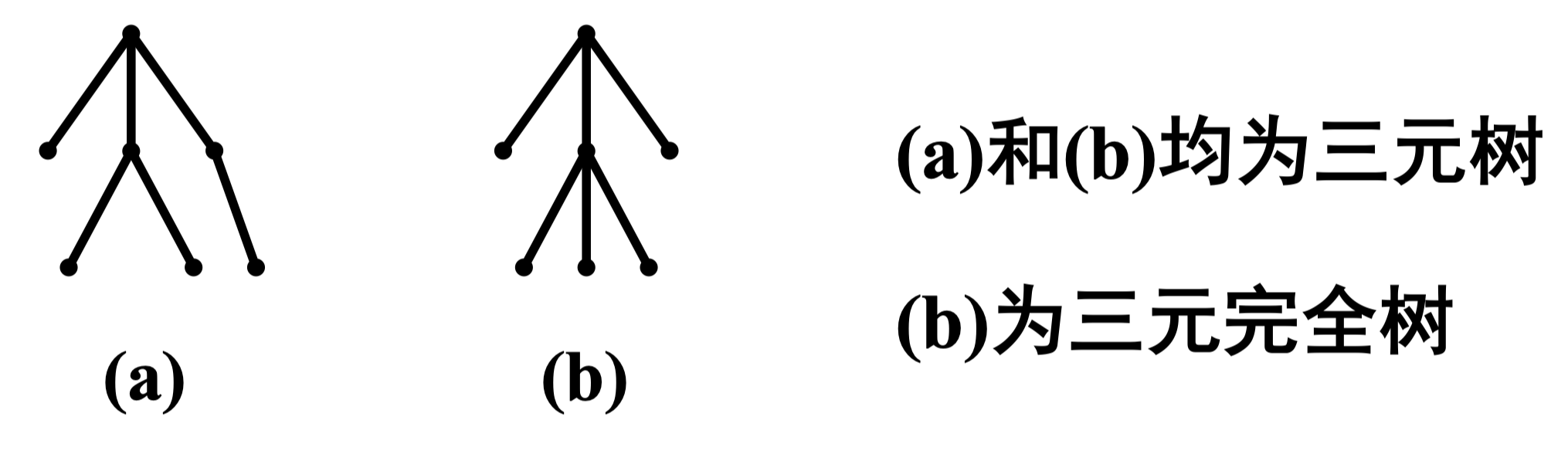
定理 125: 设 元完全树 的树叶数为 ,分支点数为 ,则
证明:由假设, 有 个顶点。再由树中点数与边数的关系知, 有 条边
因 元完全树的每个分支点的出度均为 ,叶的出度为零,从而 的所有顶点的出度之和为 。再由有向图中所有顶点的出度之和等于边数可得:
例:二元完全树 ,则分支点数为 ,边数之和为 。另外,高度为 的二元完全树最少有 片叶子
最优树
定义 141:设 是一棵有 片树叶的二元树,若对 的所有 片树叶赋以权值 (实数) ,则称 为带权二元树;若带有权 的树叶的层数为 ,则称 为 的权;给定实数 ,在所有树叶带有权 的二元树中, 最小的二元树称为最优树
例:带权二元树 , 和 如图所示,试求它们的权
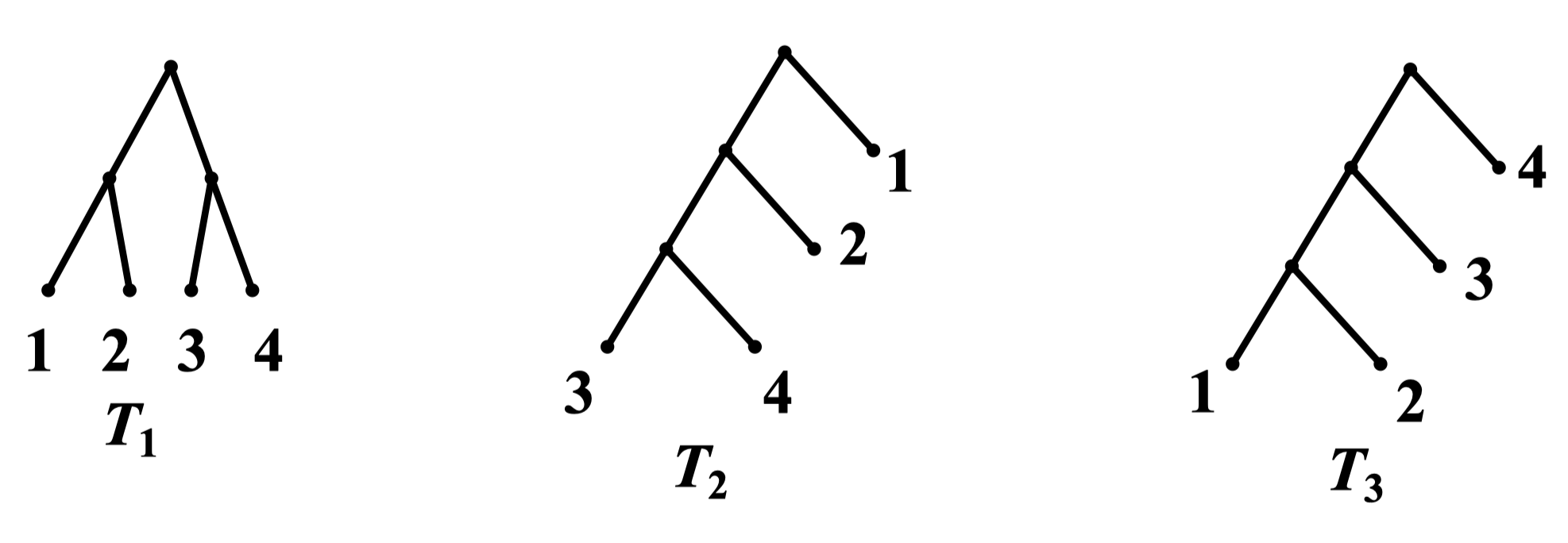
解:由带权二元树的定义,有:
实际上,对权 1,2,3,4,树 是最优树
例:求带权 1,2,4,5,6,8 的最优二元树
解:求解过程如下
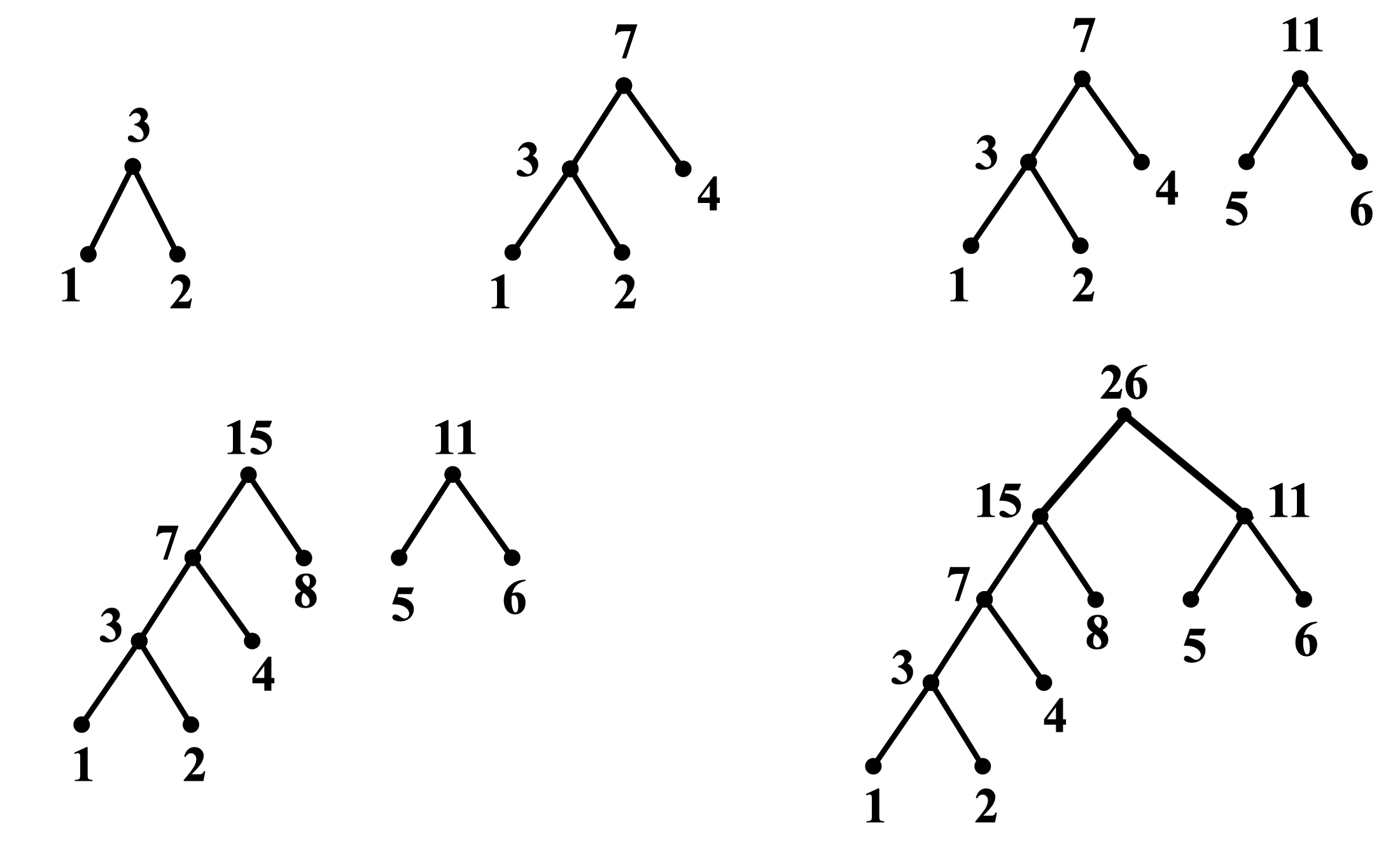
设求得的最优二元树为 ,则
 注意:
注意: 注意
注意 解释:
解释: 注意
注意 注意
注意 注意
注意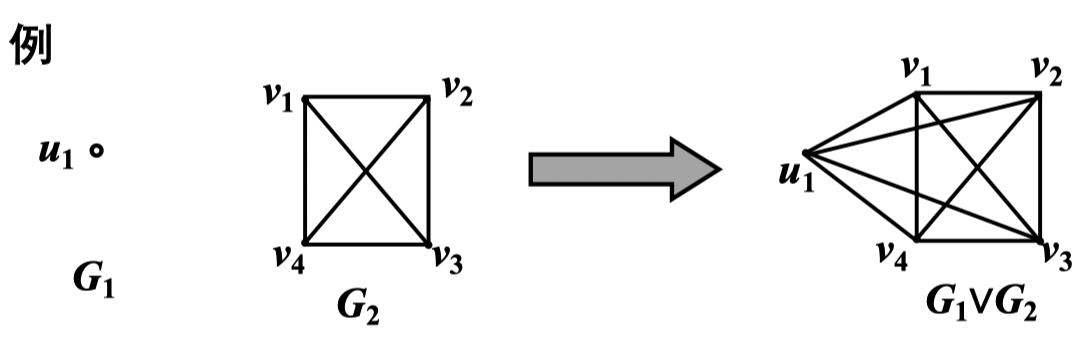
 注意
注意
 例:完全图的直径是 1
例:完全图的直径是 1







 注意
注意 注意
注意


 注:以下讨论的生成树的个数均指标定图而言。标定图的生成树的数量远大于非标定图生成树的数量。如标定图
注:以下讨论的生成树的个数均指标定图而言。标定图的生成树的数量远大于非标定图生成树的数量。如标定图 






 注:若
注:若 
 注:以上定理表明圈中的边一定不是割边,所以删去圈中的边不会破坏图的连通性
注:以上定理表明圈中的边一定不是割边,所以删去圈中的边不会破坏图的连通性 注意
注意
 注意
注意
 注:两个不同块的公共顶点只能是割点,即块与块只能由割点相联结,因此可以通过割点搜寻块
注:两个不同块的公共顶点只能是割点,即块与块只能由割点相联结,因此可以通过割点搜寻块 注意
注意
 注意
注意
 注:连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的点数”
注:连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的点数”
 注意
注意 注:对连通图
注:对连通图  注:边连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的边数”
注:边连通度也可描述为 “使图不连通或成为平凡图,最少需要删去的边数”
 注意
注意


 注:「任意两个不相邻的顶点之间存在
注:「任意两个不相邻的顶点之间存在  注意
注意



 注意
注意 注意
注意
 仅是有
仅是有  注意
注意



 注意
注意





注:上述定理只是必要条件,而非充分条件



 注:闭图的并图并 (
注:闭图的并图并 (
 注:
注:
 注:一个图的闭包不一定是完全图。比如下图中 (a)、(b) 两个均不是完全图,但它们却是自己的闭包
注:一个图的闭包不一定是完全图。比如下图中 (a)、(b) 两个均不是完全图,但它们却是自己的闭包

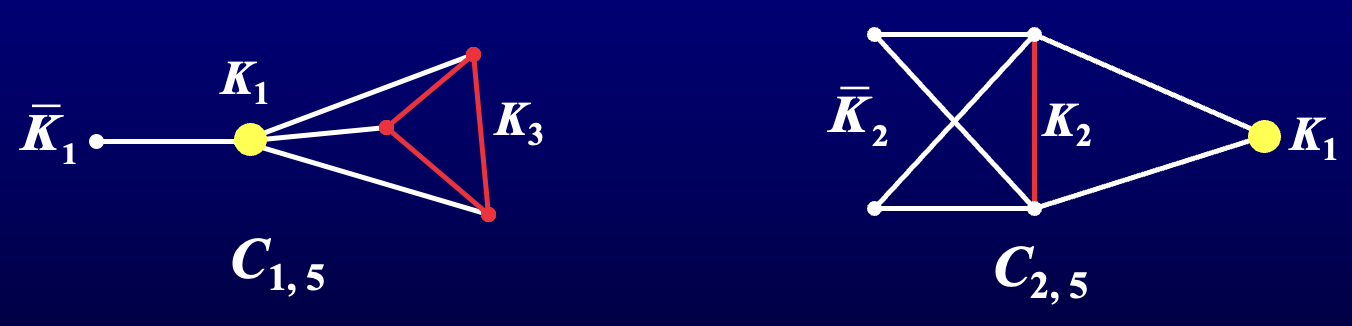
 注意
注意
 注:推论的条件是充分而非必要的。例如
注:推论的条件是充分而非必要的。例如 

 注:一般地,
注:一般地, 注:该定理的逆命题不成立
注:该定理的逆命题不成立

 注意
注意



 注意
注意

 注:有割边的 3 正则图不一定就没有完美匹配
注:有割边的 3 正则图不一定就没有完美匹配
 注意
注意

 注:1-可因子分解的 3 正则图不一定有 Hamilton 圈 (即:定理 66 返过来不一定成立)
注:1-可因子分解的 3 正则图不一定有 Hamilton 圈 (即:定理 66 返过来不一定成立)
 注:无割边的 3 正则图可能也没有 1-因子分解
注:无割边的 3 正则图可能也没有 1-因子分解

 注:若没有割边的 3-正则图中的 2-因子是一些偶圈,则该图也是 1-可因子化的
注:若没有割边的 3-正则图中的 2-因子是一些偶圈,则该图也是 1-可因子化的
 注:所有森林因子的并要等于图
注:所有森林因子的并要等于图 


 (考过) 例:证明:若
(考过) 例:证明:若 


 注:可平面图概念和平面图概念有时可以等同看待
注:可平面图概念和平面图概念有时可以等同看待
 注:每个平面图有且仅有一个外部面
注:每个平面图有且仅有一个外部面
 注意
注意

 注意
注意
 注意
注意
 注:该定理可以简单记为「极大平面图的三角形特征」,即每个面的边界是三角形
注:该定理可以简单记为「极大平面图的三角形特征」,即每个面的边界是三角形 注:顶点数相同的极大平面图并不唯一。顶点数相同的极大平面图的个数和结构问题仍在研究当中
注:顶点数相同的极大平面图并不唯一。顶点数相同的极大平面图的个数和结构问题仍在研究当中
 注:对外可平面图
注:对外可平面图 
 注:极大外平面图的外部面的边界是由多边形组成,内部面均由三角形围成
注:极大外平面图的外部面的边界是由多边形组成,内部面均由三角形围成

 注:无论
注:无论  注:同构的平面图可以有不同构的对偶图
注:同构的平面图可以有不同构的对偶图


 注:图的可平面性在同胚意义下不变
注:图的可平面性在同胚意义下不变 注:库拉托夫斯基定理可以等价叙述为:「图
注:库拉托夫斯基定理可以等价叙述为:「图 





 注:
注: 注:
注:


 注:冲突的两个片段无法同时平面嵌入到同一个面中
注:冲突的两个片段无法同时平面嵌入到同一个面中



 注:根据维津定理,简单图可以按边色数分成两类图,一是边色数等于
注:根据维津定理,简单图可以按边色数分成两类图,一是边色数等于 


 注:对图的正常顶点着色,带来的是图的顶点集合的一种划分方式。着同一种颜色的顶点集合称为一个色组,它们彼此互不相邻,所有又称为点独立集
注:对图的正常顶点着色,带来的是图的顶点集合的一种划分方式。着同一种颜色的顶点集合称为一个色组,它们彼此互不相邻,所有又称为点独立集

 注:此定理是对
注:此定理是对 
 注意
注意 注意
注意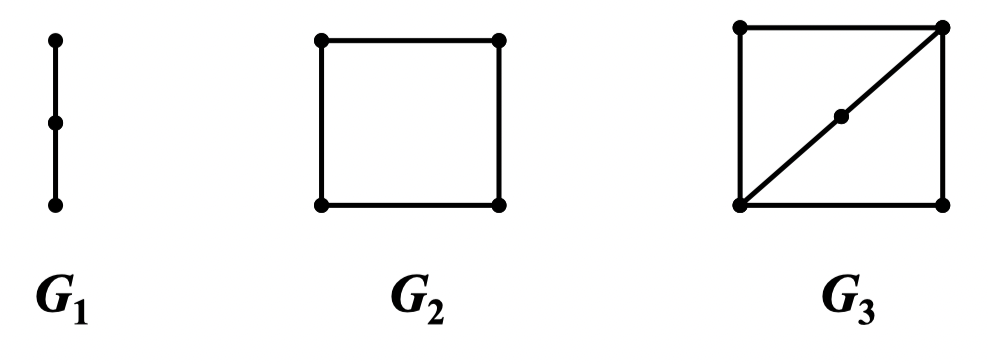
注:递推计数法的计算复杂度是指数型的

 注:上述定理实际上给出了色多项式的求法:用
注:上述定理实际上给出了色多项式的求法:用 
 注:该定理说明,在求
注:该定理说明,在求 
 注意
注意


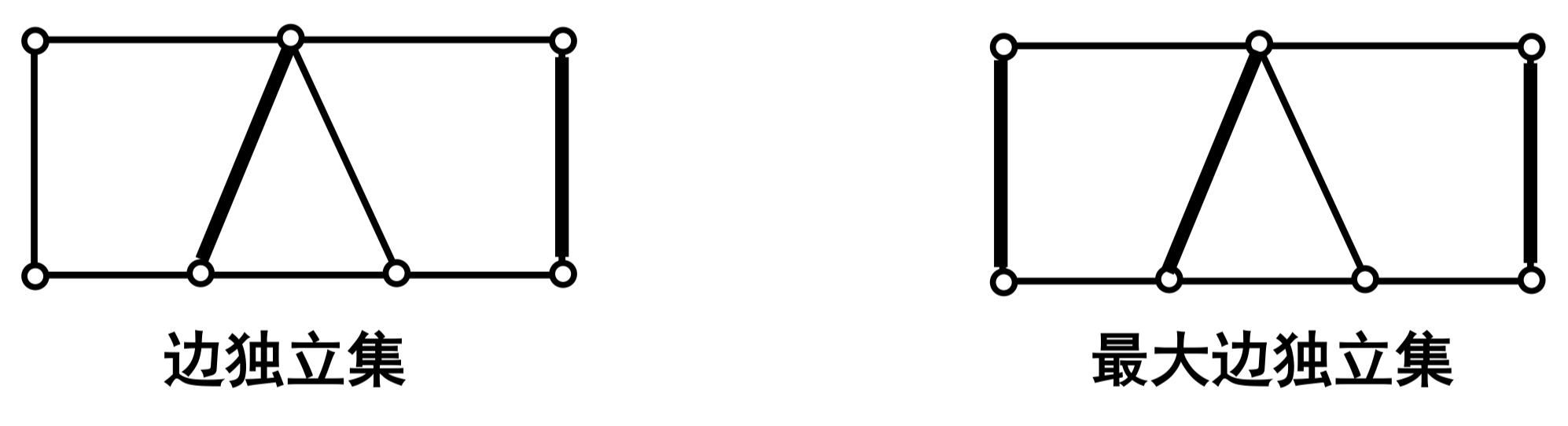
 注:一个边独立集实际上就是图的一个匹配,一个最大边独立集就是图的一个最大匹配
注:一个边独立集实际上就是图的一个匹配,一个最大边独立集就是图的一个最大匹配

 注:由定义知
注:由定义知  注:有向图的基础图唯一,而一个图的定向图并不唯一
注:有向图的基础图唯一,而一个图的定向图并不唯一


 注:若
注:若  注:强连通一定单向连通,单向连通一定弱连通
注:强连通一定单向连通,单向连通一定弱连通


 注:有向图
注:有向图