图论作业 2
一、填空题
1. 图
考点:握手定理 + 点连通度 +
连通 「一个图是
连通的,说明点连通度 」「 」 故有
所以:
所以
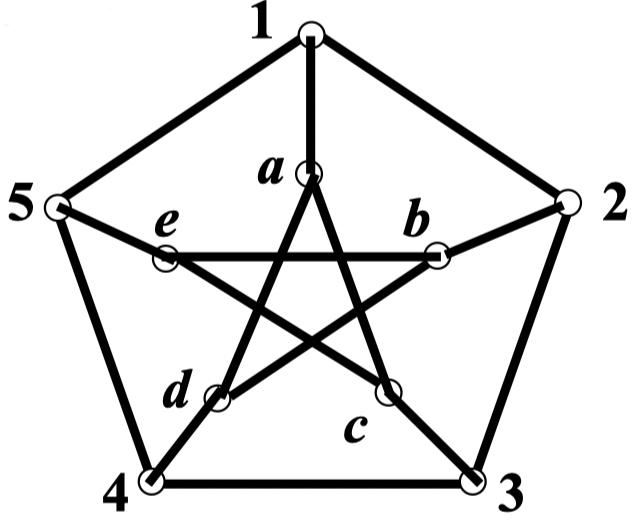
2. 彼得森图的点连通度和边连通度分别为
考点:特殊图的点连通度和边连通度
注意:特殊图有:「彼得森图」「
方图」「二部图」「完全图」 注意:总结特殊图的「点连通度」「边连通度」「点色数」「边色数」
彼得森图是
正则图,故有 彼得森图不是哈密尔顿图,但在彼得森图的基础上删去任意一个顶点后,会变成哈密尔顿图 (经过每个点的圈);如果再删去一个点,必不会改变图的点连通性,因为已经是圈了,删去一个点顶多把圈变成路。所以必有
综上:
3. 非平凡树的点连通度和边连通度分别为
对树来说,每条边都是割边,每个分支点 (度数大于 1 的顶点称为分支点) 都是割点
非平凡树首先想到完全
阶图,即
没有割点,但点连通度为 (完全图的点连通度是顶点数 ) 对于
的非平凡树,肯定有分支点,所以点连通度为 从另一个角度理解,非平凡树每条边都是割边,故
又因为有
所以有
故
4. 长度为
考点:宽距离 & 宽直径
两个顶点
的 宽距离, 间找 条独立的路,且每条路尽可能的短, 条路中最长的路就是宽距离 所有点对的
宽距离的最大值就是 宽直径 对于本题,两个点邻接时,宽距离最大,为
,故 宽直径为
5. 完全图
考点:宽距离 & 宽直径
任意两个点
的第一条路直接为相连,即 ,长度为 第二条路:任意找一个其他点
,即 ,长度为 第三条路同理。所以
宽直径为
6. 设图
奇度顶点的个数一定是偶数,不然无法满足握手定理
欧拉图的每个顶点的度数一定是偶数
7. 完全偶图
最优欧拉环游:包含该图的每条边至少一次,且边权之和最小的闭途径
特别地,对于欧拉图来说,最优欧拉环游就是欧拉回路
完全偶图
一定是欧拉图,所以 包含的边数为
8. 下图的最优欧拉环游的权值为
这样的图一定是特殊的图,恰好有一对奇度顶点
我们只需要把这对奇度顶点最短路上的边复制一次即可
9. 具有
考点:
图 注意:
图的结构和性质需要掌握 包含边数最多的非哈密尔顿图只有两类:
和
二、不定项选择题
- 下列说法正确的是(CD)
- A. 有割边的图一定有割点 ❌
- B. 有割点的图一定有割边 ❌
- C. 割点至少属于图的两个块
- D. 割边不在图的任一圈中
- E. 图的割点也是子图的割点 ❌
考点:割边 + 割点
注意 1:提到割边一定要想到「
」;提到割点一定要想到「自环」「八字形的图」「 」;提到块一定要想到「阶数至少为 3」 注意 2:两个不同块的公共顶点只能是割点,即块与块只能由割点相联结,因此可以通过割点搜寻块
A 错误:提到割边想到「
」,有割边无割点 B 错误:提到割点想到「八字形的图」,有割点没有割边
C 正确:定理 33:点
是图 的割点当且仅当 至少属于 的两个不同的块 D 正确
E 错误:八字形的图去掉一个块就没有割点
- 设
- A. 存在图
- B. 存在图
- C. 设图
- D. 图
- E. 若图
考点:点连通度 + 边连通度 + 最小度「
」 A B 显然正确
C 正确:引理:设
是 阶简单图,若 ,则 必连通 定理 37:设 是 阶简单图,若 ,则 D 错误:
E 正确
- 下面说法正确的是(BDE)
- A. 没有割点的非平凡连通图一定是
- B.
- C. 完全图一定没有割边 ❌
- D. 完全图一定没有割点
- E. 非平凡树一定有割边
- F. 非平凡树一定有割点 ❌
考点:割边 + 割点
A 错误:提到割点想到「
」,是 1 连通图;如果加上限定条件「阶数 」就是正确的 B 正确:
连通图一定是 边连通的,一定没有割边; 连通图阶数一定 ,有割边一定有割点,故矛盾! C 错误:提到割边想到「
」;如果加上限定条件「阶数 」就是正确的 D 正确
E 正确:非平凡树一定有边,每条边一定是割边
F 错误:提到割点想到「
」
- 下面说法正确的是(B)
- A. 若图
- B. 若图
- C. 若图
- D. 存在最小度为
- E. 存在具有
考点:点连通度 + 边连通度 + 点割 + 边割
注意:有些图没有点割,但其连通度为
A 错误:完全图
没有点割,但连通度为 ;换成边割就成立 B 正确 C 错误:
D 错误:最小度为
,其点连通度最多为 E 错误:
表示「平均度 + 1」,肯定大于最小度
- 设图
- A. 图中一定有圈 ❌
- B. 图中一定无环 ❌
- C. 图中一定无割边 ❌
- D. 图中一定无割点
- E. 若
- F. 若
- G. 若
考点:块
注意:提到块,一定要想到阶数至少为
- 阶数为
的块,要么是孤立点,要么是自环 - 只有一条边的块,要么是自环,要么是
A 错误:「
」;B 错误:「自环」;C 错误:「 」 D 正确:块就是没有割点的连通图
E 正确:定理 32:设图
的阶至少为 ,则 是块当且仅当 无自环并且任意两点都位于同一个圈上 F 正确:推论:设
的阶至少为 ,则 是块当且仅当 无孤立点且任意两条边都在同一个圈上 G 正确:至少有三个点的块无环、无割边
- 下面说法错误的是(AB)
- A. 顶点度数为偶数的图一定是欧拉图 ❌
- B. 欧拉图一定没有割点 ❌
- C. 欧拉图一定没有割边
- D. 非平凡欧拉图中一定有圈
- E. 至少具有
考点:欧拉图
注意:欧拉图和哈密尔顿图都有一个大前提:均为连通图
A 错误:没有说明是否连通,只能确定每个连通分支均为欧拉图
B 错误:八字形的图
C 正确:欧拉图的边集能划分为边不重的圈的并,每条边均在圈上
D 正确:只要有边,就有圈
E 正确:根据 C 选项知欧拉图一定没有割边,所以边连通一定是
思考 1:两个欧拉图的积图是否还是欧拉图?(是)
思考 2:两个哈密尔顿图的积图是否还是哈密尔顿图?(是)
- 关于哈密尔顿图,下列命题错误的是(E)
- A. 若
- B. 设
- C. 设
- D. 哈密尔顿图一定没有割边
- E. 哈密尔顿图一定没有割点 ❌
考点:哈密尔顿图
A 正确:定理 44:若
是 图,则对于 的每个非空真子集 ,均有 B 正确:定理 45 (Dirac 1952):对于
的简单图 ,如果 中有: ,那么 是 图 C 正确:定理 46 (Ore 1962):对于
的简单图 ,如果 中的任意两个不相邻顶点 与 ,有: ,那么 是 图 D 显然正确
E 错误:存在自环的哈密尔顿图有割点;哈密尔顿简单图中一定不存在割点
- 关于哈密尔顿图,下列命题正确的是(ABCE)
- A. 设
- B. 设
- C. 设
- D. 设
- E. 设
考点:闭包
注意 1:满足 Dirac 定理、Ore 定理、度序列判定定理的图的闭包一定是完全图
注意 2:定理 49 (Bondy):一个简单图
是 图当且仅当它的闭包是 图 A B C 正确
D 错误:否命题不成立
E 正确: 推论:设
是 的简单图,若 的闭包是完全图,则 是 图
- 关于哈密尔顿图,下列命题错误的是(BD)
- A. 设
- B. 图
- C. 若
- D. 若图
- E. 设
考点:哈密尔顿图 + 闭包
A 正确:定理 51 (Chvátal 1972):若
是 的非 简单图,则 度弱于某个 图 B 错误:定理 49 (Bondy):一个简单图
是 图当且仅当它的闭包是 图 C 正确:推论:设
是 阶简单图。若 且 ,则 是 图 D 错误:一个图的闭包不一定是完全图
E 正确:阶数为奇数,则哈密尔顿圈是奇圈;定理 9:一个图是偶图当且仅当它不包含奇圈
三、解答题
- (去年考过) 证明:设简单图
证明:因为简单图
是 边连通的,所以 ;同时 如果
是边割,那么 一定是最小边割,所以 如果
不是边割,那么删去 中的边后不会破坏图的连通性,所以 综上所述:
是 的某 条边构成的集合,则
- ✨ 证明:若
证明:显然:
如果
,则图 一定是完全图 ,此时图 的点连通度和最小度均为 如果
,只需证明:「任意删除 个顶点,不会破坏图的连通性」即可 任意删除
个顶点,那么只留下了 个顶点,假设为 由于
,故 中一定有一个邻接顶点留下 假设
是 的邻接顶点,如果 不是 的邻接,那么 一定与 相邻,所以 连通 假设
不是 的邻接顶点,那么 一定与 和 相邻,所以 连通 得证:「任意删除
个顶点,不会破坏图的连通性」所以 又因为
,所以 扩展 (去年考过):如果一个图
满足: ,那么一定有圈存在 在图
中找一条最长的路,假设为 ,且依次经过 因为
,那么 一定有两个邻接顶点,所以除了 一定还存在另外一个邻接顶点 假设
另外一个邻接顶点为 ,那么一定有 所以一定存在一个路
上一定存在圈
- 在
关键:建立正确的图论模型
解:以每个方格为顶点,如果两个方格恰好是某个长
宽 矩形的对角,则这两个方格之间连一条边,我们可以得到一个图,那么该图中的边与马的每一次跳动相对应 现在问题转换为了:能否连续的经过图的每条边恰好一次,即求该图是否存在欧拉迹
图中度数为
的顶点有 个,根据 推论:连通图 有 迹当且仅当 最多有两个奇点,显然不存在欧拉迹
扩展:能否通过马的跳动遍历完所有的方格?
现在问题转换为了:上述建立模型中的图是否为哈密尔顿图
- 证明:若
证明:在图
的基础上添加一个顶点 ,让点 与图 的每个顶点都相连,得到新图,记为 那么,在
中,一定存在 根据 定理 45 (Dirac 1952):对于
的简单图 ,如果 中有: ,那么 是 图,图 一定是哈密尔顿图 从图
的哈密尔顿圈上去掉新添加的顶点 ,就变成了原图 的一条哈密尔顿路
- (前年考过) 亚瑟王在王宫中召见他的
解:以骑士为顶点,如果两个骑士是友好的,那么两个骑士之间连一条边,得到的图记为
原问题转换为:判断图
是否为哈密尔顿图 由题知:
根据 定理 45 (Dirac 1952):对于
的简单图 ,如果 中有: ,那么 是 图,图 一定是哈密尔顿图 所以亚瑟王的谋士摩林能够让这些骑士围着圆桌坐下,使得每一个骑士不与他的仇人相邻