图论作业 4
一、填空题
1. 长度至少为
考点:点色数 + 边色数
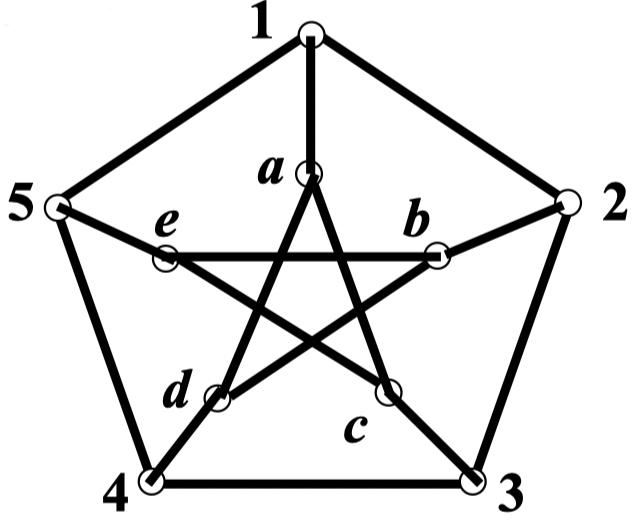
2. 彼得森图的点色数和边色数分别为
3. 已知树
考点:二部图点色数 + 边色数
二部图的点色数和边色数分别为
和最大度 一棵树肯定是二部图
4. 方体
考点:二部图点色数 + 变色数
二部图的点色数和边色数分别为
和最大度
方体是 正则二部图
5. 设
考点:独立数 + 覆盖数 = 阶数
定理 117 (Gallai):对任意的
阶图 ,有
6. 完全图
考点:二部图独立数、覆盖数
独立数
7. 已知树
考点:树的色多项式 (知道即可)
注意:树的色多项式绝对不会考
是具有 个点的树,则
8. 拉姆齐数
注意:考的概率很小
Ramsey 数 只需知道
9. 图中强连通分支的个数为
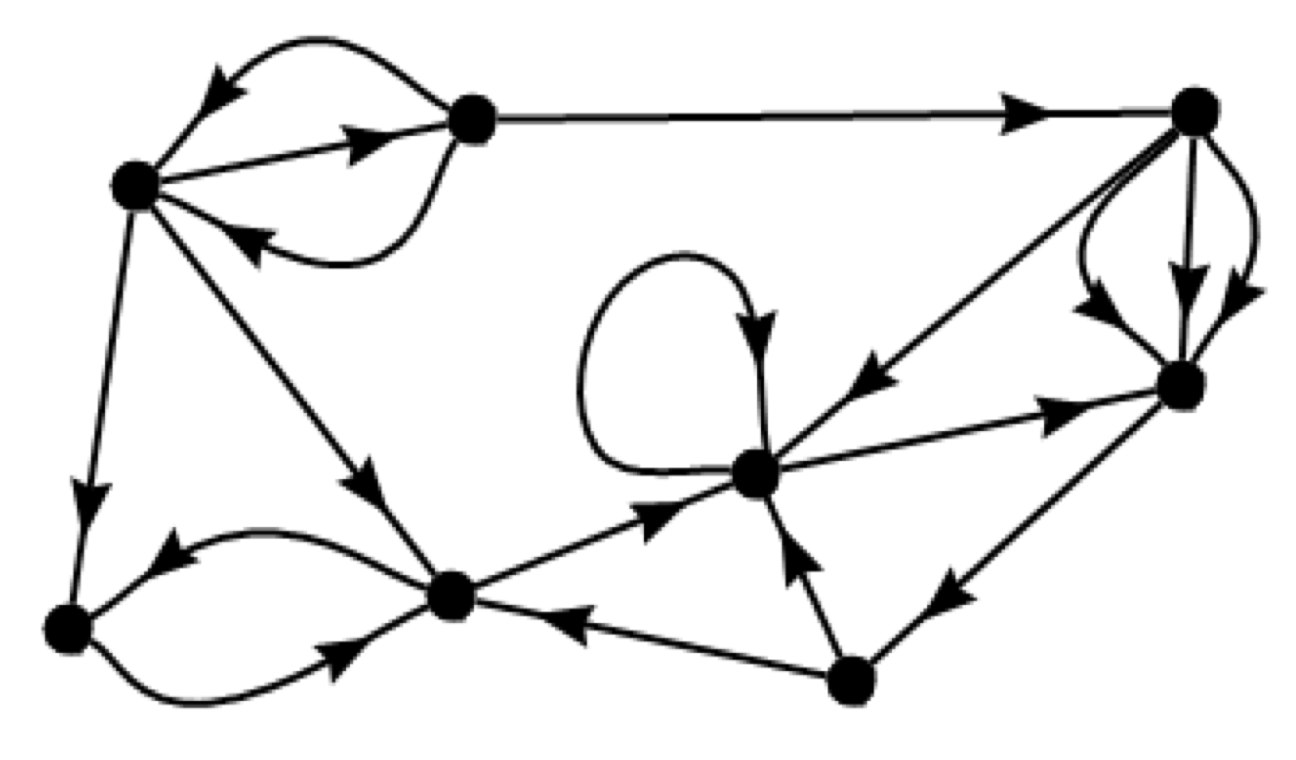
注意 (重要):判断一个有向图有多少强连通分支和单向连通分支;只能从特殊的点出发
左上角两个顶点只有出去的,没有进来的,两个点构成一个强连通分支
右上角顶点单独为一个强连通分支
剩余五个顶点被一条有向闭途径连接起来,所以在一个强连通分支中
10. 高为
叶子节点出现的越晚,叶子节点越多
例:二元完全树
,则分支点数为 ,边数之和为 。另外,高度为 的二元完全树最少有 片叶子
11. 树叶带权分别为
考点:哈夫曼编码
12. 设
定理 121: 设
是一个有向图,则有 总度数
对于树,边数 = 顶点数 - 1
顶点数 = 树叶 + 分支点 =
所以:
出度全部由于分支点,因为树叶的出度为
,所以: 所以:
13. 对具有
无环图即可
(感觉不会考 🐶)
二、不定性选择题
- 下列说法错误的是 (DG)
- A. 在正常着色下,图
- B. 若图
- C. 图
- D. 存在
- E. 所有
- F. 存在
- G. 存在
考点:关于补图的知识点
F 相关结论 (不会考):定理 91:至少有 9 个点的简单可平面图的补图是不可平面的,而 9 是这种数目中最小的一个
G 相关结论 (不会考):定理 84:每个至少有 7 个顶点的外可平面的补图不是外可平面图,且 7 是这个数目的最小者
A 正确:正常着色 (点着色),原图中每个色组中的点肯定无边相连,所以补图中一定是完全图
B 正确
C 正确:定理 6:一个
阶图 和它的补图有相同的频序列;注意是频序列,不是度序列 D 错误:定理 1:若
阶图 是自补的(即 ),则 E 正确:
是可平面图,任何一个 阶简单图一定是一个可平面图;所以 阶图的补图也一定是可平面图 F 正确:对于阶数小于
的简单可平面图,补图依然是可平面图 G 错误
- 关于完全图
- A. 点色数为
- B. 边色数为
- C. 点连通度为
- D. 边连通度为
- E. 是临界图
- F. 是唯一可着色图
考点:对完全图的理解
注意: E 和 F 涉及到第七章最后一节课讲的内容,不作要求 (临界图、唯一可着色图、不含三角形的
色图、完美图等等) A 显然正确
B 错误:根据奇偶分成两种情况
C 正确 D 正确:关于完全图,需要记住无点割,有边割
E 正确:完全图是临界图
F 正确:完全图是唯一可着色图
- 设
- A. 最小度
- B. 图
- C. 在
- D. 在
- E. 若
注意:本题涉及的知识点不考
- 下列说法正确的是 (ABCDE)
- A. 图
- B. 点子集
- C. 若图
- D. 若图
- E. 若图
A 正确:图
的独立集即为各不相邻的顶点,其补图一定都相邻,故为团 B 正确:定理 116:给定图
且 ,则 是 的独立集当且仅当 是 的覆盖 C 正确:定理 118 (Gallai):对任意不含孤立点的
阶图 ,有 D 正确:对于二部图,无论是否有孤立点,图
的边独立数等于点覆盖数(最重要,必须掌握) E 正确:定理 119: 设
是无孤立点的偶图,则 中最大独立集包含的顶点数等于最小边覆盖包含的边数
- 下列说法正确的是 (BE)
- A. 在有向图中,顶点的出度之和等于边数的两倍 ❌
- B. 在有向欧拉图中,各点的度数必为偶数
- C. 在有向图的邻接矩阵中,所有元素之和等于边数的两倍 ❌
- D. 在无环有向图的关联矩阵中,各行元素之和均等于
- E. 在无环有向图的关联矩阵中,所有元素之和等于
考点:有向图
A 错误:定理 121: 设
是一个有向图,则有 B 正确:出度 = 入度;度数 = 出度 + 入度 = 2 * 出度
C 错误:有向图的邻接矩阵中,行和 = 顶点的出度,列和 = 顶点的入度;所有元素之和 = 出度之和 = 入度之和 = 边数
D 错误:关联矩阵每一列恰有一个「1」和一个「-1」,第
行的 1 的个数等于 ,-1 的个数等于 E 正确:每一列和均为
,所以列和也为
- 对于有向图,下列说法错误的是 (D)
- A. 有向图
- B. 在有向图
- C. 有向连通图中顶点间的强连通关系是等价关系
- D. 有向连通图中顶点间的单向连通关系是等价关系 ❌
- E. 强连通图的所有顶点必然处于某一有向闭途径中
A 正确:定理 123: 有向图
的每个点位于且仅位于 的一个强 (弱) 连通分支中 B 正确:
注:有向图
的某个顶点,可能会分属于 的若干个单向连通分支。因为单向连通关系不是等价关系 C 正确
D 错误:见选项 B 分析
E 正确:定理 122: 有向图
是强连通的当且仅当 中存在含有所有顶点的有向闭途径
三、解答题
- 现有
考点:「点着色」和「边着色」应用题
注意 1:✨ 考试注意识别到底是「点着色」还是「边着色」
注意 2:考试不会超过本题的难度
本题:「边着色」
分析:以每个二人组为顶点(共 10 个),两个二人组连一条线当且仅当四个人互不相同时
解:如果两个二人组涉及到四个不同的人,这两个二人组之间连一条边,那么每一场比赛就转换成图中的一条边
原问题就转换成求该图的边色数
显然这个图为彼得森图,彼得森图的边色数是
所以最少需要安排
天的比赛
- 有
考点:点色数和边色数应用题
注意:✨ 考试注意识别到底是「点着色」还是「边着色」
解:以博士生为顶点,如果两名博士生有相同的答辩委员会成员,则连接一条边,他们的答辩时间就不能安排在一起,必须错开
如上图,点色数为
。所以,至少安排 次答辩时间段
- (19 年考过) 设
解:假设有
个分支点,那么出度之和为 出度之和 = 边数 =
得
所以
- 设
解:
后序遍历:
- 求下图的色多项式及色数
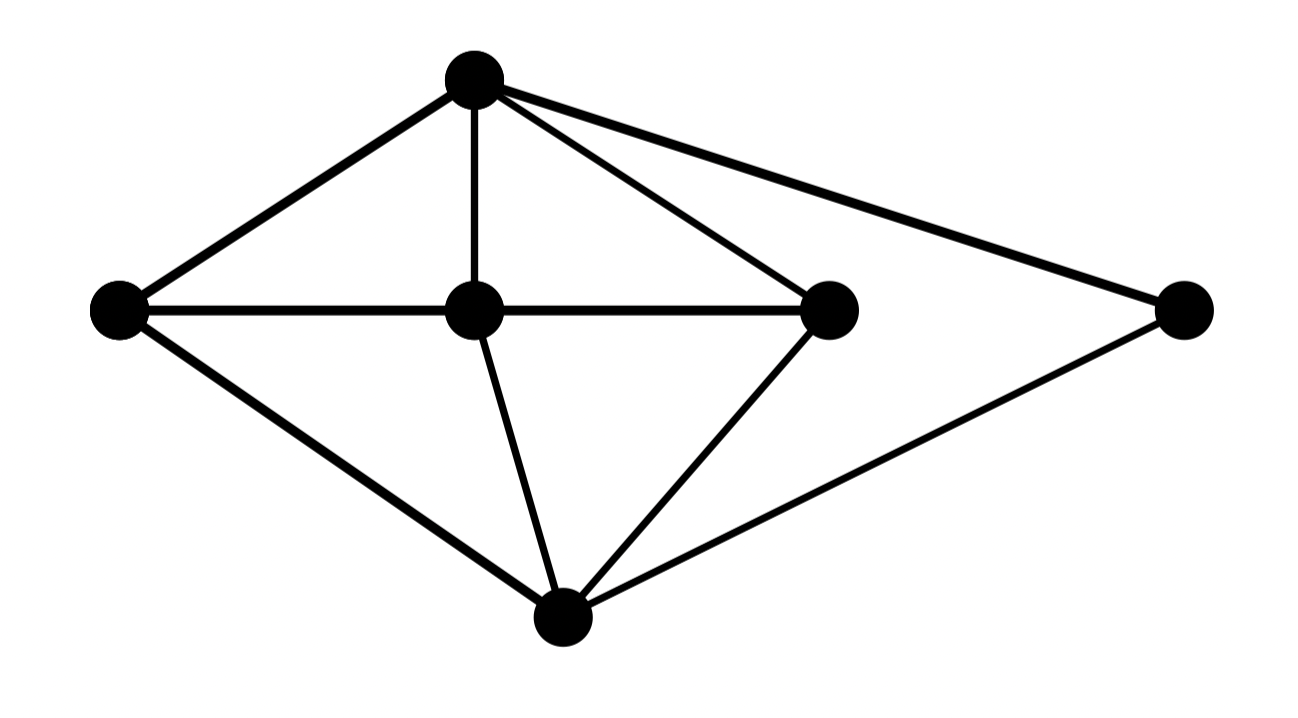
注意 1:使用的方法肯定是「递推计数法」或「理想子图法」
注意 2:先不要纠结使用什么方法,先画出补图,再决定方法
解:画出
的补图
求出补图的伴随多项式:
将
代入伴随多项式中得到 : 扩展:根据色多项式求原图的的点色数
方法:使
最小的 值,从 一个一个的试 当
时, 当
时, 当
时, 所以原图的点色数为