超级无敌精华汇总

重要结论

补图和自补图的关系

定理 1：若 $n$$n$ 阶图 $G$$G$ 是自补的（即 $G\cong \bar{G}$$G \cong \overline G$），则 $n\equiv 0,1(\mathrm{mod}4)$$n \equiv 0,1\pmod{4}$

握手定理及其推论

定理 2 (握手定理)：对任意的有 $m$$m$ 条边的图 $G=(V,E)$$G=(V,E)$，有 $\sum _{v\in V}d(v)=2m$$\sum\limits_{v \in V}d(v)=2m$

推论 1：任意图中，奇点的个数为偶数

推论 2：正则图的阶数和度数不 同时 为奇数（有歧义，注意断句！！！即阶数和度数不能均为奇数）

度序列、图序列、频序列相关结论

「度序列」和「图序列」的关系：简单图的度序列简称图序列

定理 3：非负整数组 $(d_1,d_2,\cdots ,d_n)$$(d_1,d_2,\cdots ,d_n)$ 是图的度序列的充分必要条件是：$\sum d_i$$\sum d_i$ 为偶数

定理 4 (Havel-Hakimi 定理)：设有非负整数组 $\mathrm{\Pi }=(d_1,d_2,\cdots ,d_n)$$\Pi=(d_1,d_2,\cdots,d_n)$ 满足 $n-1\ge d_1\ge d_2\ge \cdots \ge d_n，\sum d_i=2m$$n-1 \ge d_1 \ge d_2 \ge \cdots \ge d_n，\sum d_i = 2m$，则 $\mathrm{\Pi }$$\Pi$ 是可图序列的充分必要条件是：${\mathrm{\Pi }}_1=(d_2-1,d_3-1,\cdots ,d_{d_1+1}-1,d_{d_1+2},\cdots ,d_n)$$\Pi_1=(d_2-1,d_3-1,\cdots,d_{d_1+1}-1,d_{d_1+2},\cdots,d_n)$ 是可图的

定理 5：一个简单图 $G$$G$ 的 $n$$n$ 个点的度不能互不相同

定理 6：一个 $n$$n$ 阶图 $G$$G$ 和它的补图有相同的频序列

如果非负整数序列 $(d_1,d_2,\cdots ,d_n)$$(d_1,d_2,\cdots,d_n)$ 是简单图的度序列，那么在同构意义下「不」只能确定一个图

子图和生成子图的关系

$G$$G$ 的「生成子图」是指满足 $V(H)=V(G)$$V(H) = V(G)$ 的子图 $H⟹H$$H \Longrightarrow H$ 中的顶点集合和 $G$$G$ 中的顶点集合相同

具有 $m$$m$ 条边的简单标号图的生成子图的个数显然为 $2^m$$2^m$

途径 & 迹 & 路 & 圈

若图中两个不同点 $u$$u$ 与 $v$$v$ 间存在途径，则 $u$$u$ 与 $v$$v$ 间必存在路 $⟹$$\Longrightarrow$ 「途径 $\to$$\rightarrow$ 路」

若过点 $u$$u$ 存在闭迹，则过点 $u$$u$ 必存在圈 $⟹$$\Longrightarrow$ 「闭迹 $\to$$\rightarrow$ 圈」

若过点 $u$$u$ 存在闭途径，则过点 $u$$u$ 不一定存在圈 $⟹$$\Longrightarrow$ 「闭途径 $\nrightarrow$$\nrightarrow$ 圈」

图的连通性相关结论

定理 7：若图 $G$$G$ 是不连通的，则其补图是连通图

定理 8：设图 $G$$G$ 为 $n$$n$ 阶简单图，若 $G$$G$ 中任意两个不相邻顶点 $u$$u$ 与 $v$$v$ 满足 $d(u)+d(v)\ge n-1$$d(u) + d(v) \ge n-1$，则 $G$$G$ 是连通图且 $d(G)\le 2$$d(G) \le 2$

注意：若 $\delta \ge 2$$\delta \ge 2$，则 $G$$G$ 中必然含有圈

邻接矩阵相关结论

定理 10：令 $G$$G$ 是一个有推广邻接矩阵 $A$$A$ 的 $p$$p$ 阶标定图，则 $A^n$$A^n$ 的 $i$$i$ 行 $j$$j$ 列元素 $a_{ij}^{(n)}$$a^{(n)}_{ij}$ 等于由 $v_i$$v_i$ 到 $v_j$$v_j$ 的长度为 $n$$n$ 的途径的数目

推论：设 $A$$A$ 为简单图 $G$$G$ 的邻接矩阵，则：

• $A^2$$A^2$ 的元素 $a_{ii}^{(2)}$$a^{(2)}_{ii}$ 是 $v_i$$v_i$ 的度数。$A^3$$A^3$ 的元素 $a_{ii}^{(3)}$$a^{(3)}_{ii}$ 是含 $v_i$$v_i$ 的三角形的数目的两倍

简单标定图的领结矩阵的各行 (列) 元素之和是该行 (列) 对应的点的度

矩阵 $A$$A$ 的所有元素之和等于该图边数的 $2$$2$ 倍

矩阵 $A$$A$ 的所有特征值之和等于 $0$$0$

矩阵 $A$$A$ 的所有特征值的平方和等于该图边数的 $2$$2$ 倍

矩阵 $A^2$$A^2$ 的主对角线的元素之和等于该图边数的 $2$$2$ 倍

$l$$l$ 部图

完全 $l$$l$ 部图 $K_{n_1,n_2,\cdots ,n_l}$$K_{n_1,n_2,\cdots,n_l}$ 的点数：$\sum _{i=1}^l{n}_i$$\sum \limits^l_{i=1} n_i$；边数：$\sum _{1\le i<j<\le l}{n}_i{n}_j$$\sum \limits_{1\le i < j < \le l} n_in_j$

定理 14：连通偶图的 2 部划分是唯一的

定理 15：$n$$n$ 阶完全偶图 $K_{n_1,n_2}$$K_{n_1,n_2}$ 的边数 $m=n_1{n}_2$$m=n_1n_2$，且 $m\le \lfloor n^2/4\rfloor$$m \le \lfloor n^2/4 \rfloor$

Turán 定理

定理 18 (Turán)：若 $G$$G$ 是 $n$$n$ 阶简单图，并且不包含 $K_{l+1}$$K_{l+1}$，则边数 $m(G)\le m(T_{l,n})$$m(G) \le m(T_{l,n})$。此外，仅当 $G\cong T_{l,n}$$G \cong T_{l,n}$ 时，$m(G)=m(T_{l,n})$$m(G)=m(T_{l,n})$

✨ 计算公式： $K_{l+1}\notin G$$K_{l+1} \notin G$，则 $m(T_{l,n})=C_l^2(n/l{)}^2$$m(T_{l,n}) = C^2_l (n/l)^2$

例： $n$$n$ 阶简单图 $G$$G$，$K_3\notin G$$K_3 \notin G$，则 $G$$G$ 最多有 $\lfloor n^2/4\rfloor$$\left \lfloor n^2/4 \right \rfloor$ 条边 $\Rightarrow m(G)\le m(T_{2,n})=C_2^2(n/2{)}^2=(n/2{)}^2$$\Rightarrow m(G) \le m(T_{2,n}) = C^2_2(n/2)^2 = (n/2)^2$

例： 9 阶简单图 $G$$G$，$K_4\notin G$$K_4 \notin G$，则 $G$$G$ 最多有 27 条边 $\Rightarrow m(G)\le m(T_{3,9})=C_3^2(9/3{)}^2=3\times (9/3{)}^2=27$$\Rightarrow m(G) \le m(T_{3,9}) = C^2_3(9/3)^2 = 3 \times (9/3)^2 = 27$

树的相关结论

「树」是连通的无圈图（连通 + 无圈 两者缺一不可）；「森林」是在树的基础上无连通的约束

「树」与「森林」都是偶图

定理 20：每棵非平凡树至少有两片树叶

• 如果正整数序列 $(d_1,d_2,\cdots ,d_n)$$(d_1,d_2,\cdots,d_n)$是一棵树的度序列且 $n\ge 2$$n \ge 2$，那么序列中至少有两个 $1$$1$

定理 21：设 $G$$G$ 是具有 $n$$n$ 个点 $m$$m$ 条边的图，则下列命题等价：

• $G$$G$ 是树
• $G$$G$ 无环且任意两个不同点之间存在唯一的路
• $G$$G$ 连通，删去任一边便不连通
• $G$$G$ 连通，且 $n=m+1$$n=m+1$
• $G$$G$ 无圈，且 $n=m+1$$n=m+1$
• $G$$G$ 无圈，添加任何一条边可得唯一的圈

定理 27：$\tau (K_n)=n^{n-2}$$\tau(K_n)=n^{n-2}$

非同构的 $4$$4$ 阶和 $5$$5$ 阶树的个数分别为 $2$$2$ 和 $3$$3$

树的边数 = 顶点数 - 1

森林的边数 = 顶点数 - 连通分支数

一棵树有 $n_i$$n_i$ 个度为 $i$$i$ 的结点，$i=2,3,\cdots ,k$$i=2,3,\cdots,k$，则它有 $\sum _{i=2}^k{n}_i(i-2)+2$$\sum\limits^k_{i=2}n_i(i-2)+2$ 个度数为 $1$$1$ 的顶点

树的中心 & 形心 概念掌握即可

最小生成树的三种算法「Kruskal 算法」「破圈法」「Prim 算法」

欧拉图相关结论

定理 42：假定 $G$$G$ 是一个连通图，则下列命题等价：

• $G$$G$ 是欧拉图
• $G$$G$ 的每个点的度数是偶数
• $G$$G$ 的边集能划分为边不重的圈的并

推论：连通图 $G$$G$ 有 $Euler$$Euler$ 迹当且仅当 $G$$G$ 最多有两个奇点（ 仅是有 $Euler$$Euler$ 迹，而非 $Euler$$Euler$ 图）

当 $n$$n$ 满足什么条件时，完全图 $K_n$$K_n$ 是欧拉图？ $\to n$$\rightarrow \ \ n$ 为奇数

当 $n$$n$ 满足什么条件时，完全图 $n$$n$ 方体 $Q_n$$Q_n$ 是欧拉图？ $\to n$$\rightarrow \ \ n$ 为偶数

若完全二部图 $K_{a,b}$$K_{a,b}$ 为欧拉图，$a$$a$ 和 $b$$b$ 需满足什么条件？ $\to a,b$$\rightarrow \ \ a,b$ 均为偶数

假设图 $G$$G$ 恰好有两个连通分支，并且每个连通分支都是欧拉图，若要将 $G$$G$ 变为欧拉图，最少需要添加几条边？ $\to$$\rightarrow$ 最少需要添加 2 条边

欧拉图是否存在割边？ $\to$$\rightarrow$ 不存在

哈密尔顿图相关结论

当 $n\ge 3$$n \ge 3$ 时，完全图 $K_n$$K_n$ 是否为哈密尔顿图？ $\to$$\rightarrow \ \ $是

当 $n\ge 2$$n\ge 2$ 时，$n$$n$ 方体 $Q_n$$Q_n$ 是否为哈密尔顿图？ $\to$$\rightarrow \ \ $是

若完全二部图 $K_{a,b}$$K_{a,b}$ 为哈密尔顿图，$a$$a$ 和 $b$$b$ 需满足什么条件？ $\to a=b\ge 2$$\rightarrow \ \ a=b\ge 2$

是否存在一个具有奇数个顶点的连通图，它既是二部图，也是哈密尔顿图？ $\to$$\rightarrow \ \ $不存在，否则二部图中出现了奇圈

定理 44：若 $G$$G$ 是 $H$$H$ 图，则对于 $V$$V$ 的每个非空真子集 $S$$S$，均有 $\omega (G-S)\le |S|$$\omega(G-S)\le|S|$

• 彼得森图不是 $H$$H$ 图，但满足定理 44 中的条件

若连通图 $G$$G$ 不是 2-连通的，则 $G$$G$ 不是哈密尔顿图

哈密尔顿简单图中一定不存在割点

定理 45 (Dirac 1952)：对于 $n\ge 3$$n \ge 3$ 的简单图 $G$$G$，如果 $G$$G$ 中有：$\delta (G)\ge \frac{n}{2}$$\delta(G)\ge \frac{n}{2}$，那么 $G$$G$ 是 $H$$H$ 图

定理 46 (Ore 1962)：对于 $n\ge 3$$n \ge 3$ 的简单图 $G$$G$，如果 $G$$G$ 中的任意两个不相邻顶点 $u$$u$ 与 $v$$v$，有：$d(u)+d(v)\ge n$$d(u)+d(v) \ge n$，那么 $G$$G$ 是 $H$$H$ 图

引理：设 $G$$G$ 是 $n$$n$ 阶简单图，$u$$u$ 和 $v$$v$ 是 $G$$G$ 中不相邻的顶点，且满足 $d(u)+d(v)\ge n$$d(u)+d(v)\ge n$，则 $G$$G$ 是 $H$$H$ 图的充要条件是 $G+uv$$G+uv$ 为 $H$$H$ 图

定理 49 (Bondy)：一个简单图 $G$$G$ 是 $H$$H$ 图当且仅当它的闭包是 $H$$H$ 图

推论：设 $G$$G$ 是 $n\ge 3$$n\ge 3$ 的简单图，若 $G$$G$ 的闭包是完全图，则 $G$$G$ 是 $H$$H$ 图

推论：设 $G$$G$ 是 $n\ge 3$$n\ge 3$ 的简单图

• 若 $G$$G$ 中每个点的度 $d(v)\ge n/2$$d(v) \ge n/2$，则 $G$$G$ 是 $H$$H$ 图
• 若 $G$$G$ 中任何两个不邻接的点 $u$$u$ 和 $v$$v$ 均有 $d(u)+d(v)\ge n$$d(u)+d(v)\ge n$，则 $G$$G$ 是 $H$$H$ 图

定理 50 (度序列判定法)：设简单图 $G$$G$ 的度序列是 $(d_1,d_2,\cdots ,d_n)$$(d_1,d_2,\cdots,d_n)$，这里，$d_1\le d_2\le \cdots \le d_n$$d_1\le d_2\le \cdots \le d_n$ 并且 $n\ge 3$$n\ge 3$。若对任意的 $k<n/2$$k<n/2$，或有 $d_k>k$$d_k > k$，或有 $d_{n-k}>n-k$$d_{n-k} > n-k$，则 $G$$G$ 是 $H$$H$ 图

定理 51 (Chvátal 1972)：若 $G$$G$ 是 $n\ge 3$$n\ge 3$ 的非 $H$$H$ 简单图，则 $G$$G$ 度弱于某个 $C_{m,n}$$C_{m,n}$ 图

推论：设 $G$$G$ 是 $n$$n$ 阶简单图。若 $n\ge 3$$n\ge 3$ 且

则 $G$$G$ 是 $H$$H$ 图；并且，具有 $n$$n$ 个顶点，$\left(\begin{array}{c}n-1\\ 2\end{array}\right)+1$$\begin{pmatrix}n-1 \\2\end{pmatrix}+1$ 条边的非 $H$$H$ 图只有 $C_{1,n}$$C_{1,n}$ 以及 $C_{2,5}$$C_{2,5}$

闭包相关结论

注：一个图的闭包不一定是完全图。比如下图中 (a)、(b) 两个均不是完全图，但它们却是自己的闭包

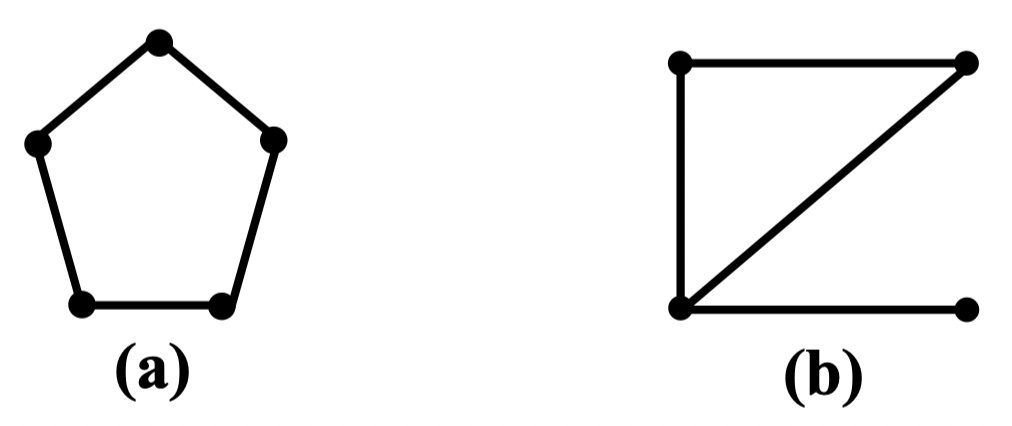
定理 48：任意图 $G$$G$ 的闭包是唯一的

匹配与因子分解

定理 59 (Berge 1957)：图 $G$$G$ 的匹配 $M$$M$ 是最大匹配当且仅当 $G$$G$ 中不含 $M$$M$ 可扩路

定理 60 (Hall 1935)：设 $G$$G$ 为具有二分类 $(X,Y)$$(X,Y)$ 的偶图，则 $G$$G$ 包含饱和 $X$$X$ 的每个顶点的匹配当且仅当 $|N(S)|\ge |S|$$|N(S)|\ge |S|$ 对所有 $S\subseteq X$$S \subseteq X$ 成立

推论：若 $G$$G$ 是 $k$$k$ 正则偶图 $(k>0)$$(k>0)$，则 $G$$G$ 有完美匹配

每个 $n$$n$ 方体都有完美匹配 $(n\ge 1)$$(n\ge 1)$

$K_{2n}$$K_{2n}$ 和 $K_{n,n}$$K_{n,n}$ 中不同的完美匹配的个数分别为 $(2n-1)!!$$(2n-1)!!$ 和 $n!$$n!$

非平凡树至多存在一个完美匹配

定理 61：设 $M$$M$ 是匹配，$K$$K$ 的覆盖，若 $|M|=|K|$$|M|=|K|$，则 $M$$M$ 是最大匹配，且 $K$$K$ 是最小覆盖

定理 62 (König 1931)：在偶图中，最大匹配中的边数等于最小覆盖中的点数

定理 63 (Tutte)：偶数阶图 $G$$G$ 有完美匹配当且仅当 $o(G-S)\le |S|$$o(G-S)\le|S|$，对所有 $S\subset V$$S\subset V$ 成立

推论 (Peterson)：每个没有割边的 3 正则图都有完美匹配

有割边的 3 正则图不一定就没有完美匹配

定理 64：完全图 $K_{2n}$$K_{2n}$ 是 1-可因子化的

定理 65： $k$$k$ 正则偶图 $(k>0)$$(k>0)$ 是 1-可因子化的

定理 66：具有 Hamilton 圈的 3 正则图是 1-可因子化的

1-可因子分解的 3 正则图不一定有 Hamilton 圈

定理 67：若 3 正则图有割边，则不可 1-因子分解

无割边的 3 正则图可能也没有 1-因子分解 (如：彼得森图)

定理 68：图 $K_{2n+1}$$K_{2n+1}$ 是 $n$$n$ 个 $H$$H$ 圈的并

定理 69：完全图 $K_{2n}$$K_{2n}$ 是一个 1-因子和 $n-1$$n-1$ 个 $H$$H$ 圈的并

定理 70：每一个没有割边的 3-正则图是一个 1-因子和一个 2-因子的并

彼得森图是一个 1-因子和一个 2-因子的并

若没有割边的 3-正则图中的 2-因子是一些偶圈，则该图也是 1-可因子化的

定理 71：一个连通图是 2-可因子化的当且仅当它是偶数度正则图

(考过证明) 若 $n$$n$ 为偶数且 $\delta (G)\ge \frac{n}{2}+1$$\delta(G) \ge \frac{n}{2} + 1$，则 $n$$n$ 阶图 $G$$G$ 有 3-因子

平面图和对偶图

定理 75：设 $G$$G$ 是具有 $m$$m$ 条边的平面图，则 $\sum _{f\in \mathrm{\Phi }}deg(f)=2m$$\sum\limits_{f \in \Phi}deg(f) = 2m$

定理 76 (Euler 公式)：设 $G$$G$ 是具有 $n$$n$ 个点，$m$$m$ 条边，$\phi$$\varphi$ 个面的连通平面图，则有 $n-m+\phi =2$$n-m+\varphi =2$

推论：设 $G$$G$ 是具有 $n$$n$ 个点，$m$$m$ 条边，$\phi$$\varphi$ 个面，$k$$k$ 个连通分支的平面图，则 $n-m+\phi =k+1$$n-m+\varphi = k + 1$

推论：设 $G$$G$ 是具有 $n$$n$ 个点，$m$$m$ 条边的简单平面图且 $n\ge 3$$n\ge 3$，则 $m\le 3n-6$$m\le 3n-6$

$K_{3,3}$$K_{3,3}$ 和 $K_5$$K_5$ 是非可平面图

定理 77：设 $G$$G$ 是简单平面图，则 $\delta \le 5$$\delta \le 5$

定理 78：一个连通平面图 $G$$G$ 是 2 连通的当且仅当 $G$$G$ 的每个面的边界是圈

定理 81：设 $G$$G$ 是至少有 3 个顶点的平面图，则 $G$$G$ 是极大平面图的充分必要条件为 $G$$G$ 中各面次数均为 3 且为简单图

推论：设 $G$$G$ 是一个有 $n$$n$ 个点，$m$$m$ 条边，$\phi$$\varphi$ 个面的极大平面图，且 $n\ge 3$$n\ge 3$，则 (1) $m=3n-6$$m = 3n - 6$；(2) $\phi =2n-4$$\varphi = 2n - 4$

定理 84：每个至少有 7 个顶点的外可平面的补图不是外可平面图，且 7 是这个数目的最小者

定理 85：平面图 $G$$G$ 的对偶图 $G^{\ast }$$G^*$ 也是平面图，并且还有

• $G^{\ast }$$G^*$ 的点数 = $G$$G$ 的面数
• $G^{\ast }$$G^*$ 的边数 = $G$$G$ 的边数
• $G^{\ast }$$G^*$ 的面数 = $G$$G$ 的点数 ($G$$G$ 连通)
• $d(v_i^{\ast })=deg(f_i)$$d(v_i^*) = deg(f_i)$

定理 86：设 $G^{\ast }$$G^*$ 是平面图 $G$$G$ 的对偶图，则 $G^{\ast }$$G^*$ 必连通

定理 87：假定 $G$$G$ 是平面图，则 $(G^{\ast }{)}^{\ast }=G$$(G^*)^*=G$ 当且仅当 $G$$G$ 是连通图

定理 88 (库拉托夫斯基定理)：图 $G$$G$ 是可平面的当且仅当它不含与 $K_5$$K_5$ 或 $K_{3,3}$$K_{3,3}$ 同胚的子图

思考：若图 $G$$G$ 与 $K_5$$K_5$ 或 $K_{3,3}$$K_{3,3}$ 同胚，则至少从 $G$$G$ 中删去 1 条边才可能使其成为可平面图

定理 90 (瓦格纳定理)：简单图 $G$$G$ 是可平面图当且仅当它不含可收缩到 $K_5$$K_5$ 或 $K_{3,3}$$K_{3,3}$ 的子图

定理 91：至少有 9 个点的简单可平面图的补图是不可平面的，而 9 是这种数目中最小的一个

着色问题

定理 101 (König)：若图 $G$$G$ 是偶图，则 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }$$\chi^{'}=\Delta$

定理 102 (Vizing)：若图 $G$$G$ 是简单图，则 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }$$\chi^{'}=\Delta$ 或 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }+1$$\chi^{'}=\Delta + 1$

定理 103：若 $G$$G$ 是非空简单图。若 $G$$G$ 中恰有一个度为 $\mathrm{\Delta }(G)$$\Delta(G)$ 的点，或 $G$$G$ 中恰有两个度为 $\mathrm{\Delta }(G)$$\Delta(G)$ 的点并且这两个点相邻，则 ${\chi }^{{}^{\prime }}(G)=\mathrm{\Delta }(G)$$\chi^{'}(G)=\Delta(G)$

定理 104：若图 $G=(V,E)$$G=(V,E)$ 是 $n$$n$ 阶简单图，若 $n=2k+1$$n=2k+1$ 且边数 $m>k\mathrm{\Delta }$$m > k\Delta$，则 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }+1$$\chi^{'}=\Delta + 1$

引理：设 $G$$G$ 是奇阶 $\mathrm{\Delta }$$\Delta$ 正则简单图。若 $\mathrm{\Delta }>0$$\Delta>0$，则 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }+1$$\chi^{'}=\Delta + 1$

定理 106：对任意的无环图 $G$$G$，均有 $\chi \le \mathrm{\Delta }+1$$\chi \le \Delta + 1$

定理 107 (Brooks)：设 $G$$G$ 是简单连通图。假定 $G$$G$ 既不是完全图又不是奇圈，则 $\chi \le \mathrm{\Delta }$$\chi \le \Delta$

Ramsey 定理

定理 116：给定图 $G=(V,E)$$G=(V,E)$ 且 $S\subseteq V$$S \subseteq V$，则 $S$$S$ 是 $G$$G$ 的独立集当且仅当 $V\setminus S$$V\setminus S$ 是 $G$$G$ 的覆盖

定理 117 (Gallai)：对任意的 $n$$n$ 阶图 $G$$G$，有 $\alpha (G)+\beta (G)=n$$\alpha(G) + \beta(G) = n$

定理 118 (Gallai)：对任意不含孤立点的 $n$$n$ 阶图 $G$$G$，有 ${\alpha }^{{}^{\prime }}(G)+{\beta }^{{}^{\prime }}(G)=n$$\alpha^{'}(G) + \beta^{'}(G) = n$

定理 119: 设 $G$$G$ 是无孤立点的偶图，则 $G$$G$ 中最大独立集包含的顶点数等于最小边覆盖包含的边数

$R(3,3)=6;R(4,4)=18$$R(3,3)=6; \ R(4,4)=18$

根树问题

定理 125: 设 $m$$m$ 元完全树 $T$$T$ 的树叶数为 $t$$t$，分支点数为 $i$$i$，则 $(m-1)i=t-1$$(m-1)i = t - 1$

例：二元完全树 $(m=2)$$(m = 2)$，则分支点数为 $i=t-1$$i = t−1$，边数之和为 $m(T)=2(t-1)$$m(T) = 2(t − 1)$。另外，高度为 $h$$h$ 的二元完全树最少有 $h+1$$h + 1$ 片叶子

特殊图总结

偶图

定理 9：一个图是偶图当且仅当它不包含奇圈

定理 14：连通偶图的 2 部划分是唯一的

定理 15：$n$$n$ 阶完全偶图 $K_{n_1,n_2}$$K_{n_1,n_2}$ 的边数 $m=n_1{n}_2$$m=n_1n_2$，且 $m\le \lfloor n^2/4\rfloor$$m \le \lfloor n^2/4 \rfloor$

若 $G$$G$ 为 $k$$k$ 正则二部图 $(k\ge 2)$$(k \ge 2)$，则 $G$$G$ 无割边

是否存在一个具有奇数个顶点的连通图，它既是二部图，也是哈密尔顿图？ $\to$$\rightarrow \ \ $不存在，否则二部图中出现了奇圈

若二部图 $G$$G$ 是哈密尔顿图，则它的二部划分 $(X,Y)$$(X,Y)$ 满足什么条件？ $\to |X|=|Y|$$\rightarrow \ \ |X|=|Y|$

定理 60 (Hall 1935)：设 $G$$G$ 为具有二分类 $(X,Y)$$(X,Y)$ 的偶图，则 $G$$G$ 包含饱和 $X$$X$ 的每个顶点的匹配当且仅当 $|N(S)|\ge |S|$$|N(S)|\ge |S|$ 对所有 $S\subseteq X$$S \subseteq X$ 成立

推论：若 $G$$G$ 是 $k$$k$ 正则偶图 $(k>0)$$(k>0)$，则 $G$$G$ 有完美匹配

定理 62 (König 1931)：在偶图中，最大匹配中的边数等于最小覆盖中的点数

图 $K_{m,n}(m\le n)$$K_{m,n}(m \le n)$ 的「最大匹配包含的边数」和「最小覆盖包含的点数」均为 $m$$m$

定理 65： $k$$k$ 正则偶图 $(k>0)$$(k>0)$ 是 1-可因子化的

推论：完全图和完全偶图的荫度为 $\sigma (K_n)=\lceil \frac{n}{2}\rceil ,\sigma (K_{r,p})=\lceil \frac{rp}{r+p-1}\rceil$$\sigma(K_n)=\lceil \frac{n}{2} \rceil , \ \ \sigma(K_{r,p})=\lceil \frac{rp}{r+p-1} \rceil$

定理 101 (König)：若图 $G$$G$ 是偶图，则 ${\chi }^{{}^{\prime }}=\mathrm{\Delta }$$\chi^{'}=\Delta$

对于 $K_{m,n}$$K_{m,n}$，${\chi }^{{}^{\prime }}(K_{m,n})=\mathrm{\Delta }$$\chi^{'}(K_{m,n})=\Delta$

定理 119: 设 $G$$G$ 是无孤立点的偶图，则 $G$$G$ 中最大独立集包含的顶点数等于最小边覆盖包含的边数

完全图

完全图的直径是 $1$$1$

$K_n$$K_n$ 的邻接谱：$\begin{array}{c}Spec(K_n)=\left(\begin{array}{cc}-1& n-1\\ n-1& 1\end{array}\right)\end{array}$$Spec(K_n) = \begin{pmatrix} -1 & n-1 \\ n-1 & 1 \end{pmatrix}$

• 重数：$\lambda$$\lambda$ 不同值出现的次数
• $Spec(K_n)$$Spec(K_n)$：第一行是特征值；第二行是重数
• 注意：只需要掌握 $K_n$$K_n$ 的邻接谱即可

对于任意的 $w(2\le w\le n-1)$$w \ (2\le w\le n-1)$，任意点对间的 $w$$w$ 宽距离为 $2$$2$，即：$d_w(K_n)=2(2\le w\le n-1)$$d_w(K_n)=2 \ (2\le w \le n-1)$

完全图的边色数为 $n-1(n\text{为}\text{偶}\text{数})$$n - 1 \ (n 为偶数)$ 或 $n(n\text{为}\text{奇}\text{数})$$n \ (n 为奇数)$，点色数为 $n$$n$

完全图的点连通度和边连通度分别为 $n-1$$n-1$ 和 $n-1$$n-1$

彼得森图

彼得森图不是 $H$$H$ 图

彼得森图有完美匹配

彼得森图不可 1-因子分解

彼得森图不可平面图

彼得森图的边色数为 $4$$4$，点色数为 $3$$3$

彼得森图的点连通度和边连通度分别为 $3$$3$ 和 $3$$3$

$n$$n$ 方体

重要知识梳理（选择 & 填空）

图的基本概念

$3$$3$ 个顶点的非同构的所有简单图有 $4$$4$ 个，$4$$4$ 个顶点的非同构的所有简单图有 $11$$11$ 个

具有 $m$$m$ 条边的简单标号图的生成子图的个数显然为 $2^m$$2^m$

图 $G_1=(n_1,m_1)$$G_1=(n_1, m_1)$ 与图 $G_2=(n_2,m_2)$$G_2=(n_2, m_2)$ 的积图 $G_1\times G_2$$G_1\times G_2$ 的点数为 $n_1{n}_2$$n_1n_2$，边数为 $n_1{m}_2+n_2{m}_1$$n_1m_2+ n_2m_1$

图 $G_1=(n_1,m_1)$$G_1=(n_1, m_1)$ 与图 $G_2=(n_2,m_2)$$G_2=(n_2, m_2)$ 的联图 $G_1\vee G_2$$G_1\vee G_2$ 的点数为 $n_1+n_2$$n_1 + n_2$，边数为 $m_1+m_2+n_1{n}_2$$m_1+ m_2+ n_1n_2$

超立方体 $Q_n$$Q_n$ 是具有 $2^n$$2^n$ 个顶点，$n{2}^{n-1}$$n2^{n-1}$条边的 $n$$n$ 正则二部图

$A^2$$A^2$ 的元素 $a_{ii}^{(2)}$$a^{(2)}_{ii}$ 是 $v_i$$v_i$ 的度数。$A^3$$A^3$ 的元素 $a_{ii}^{(3)}$$a^{(3)}_{ii}$ 是含 $v_i$$v_i$ 的三角形的数目的两倍

矩阵 $A$$A$ 的所有特征值的平方和等于该图边数的 $2$$2$ 倍

$K_n$$K_n$ 的最大特征值为 $n-1$$n − 1$

若图 $G$$G$ 度弱于图 $H$$H$，则图 $G$$G$ 的边数小于等于图 $H$$H$ 的边数

树

非平凡树至多存在一个完美匹配

非同构的 $4$$4$ 阶、$5$$5$ 阶、$6$$6$ 阶树的个数分别为 $2$$2$、$3$$3$、$6$$6$

由 $k$$k$ 颗树组成的森林满足 $m=n-k$$m = n − k$

非平凡树的点连通度和边连通度分别为 $1$$1$ 和 $1$$1$

$\tau (K_n)=n^{n-2};\tau (K_{m,n})=n^{m-1}{m}^{n-1}$$\tau(K_n)=n^{n-2}; \ \ \tau(K_{m,n})=n^{m-1}m^{n-1}$

• $K_5=125;K_{3,3}=81$$K_5 = 125; \ \ K_{3,3}=81$

图的连通性

定理 34：对任意的图 $G$$G$，有 $\kappa (G)\le \lambda (G)\le \delta (G)$$\kappa (G) \le \lambda (G) \le \delta(G)$

定理 35：设 $G$$G$ 是具有 $m$$m$ 条边的 $n$$n$ 阶连通图，则 $\kappa (G)\le \lfloor 2m/n\rfloor$$\kappa (G) \le \left \lfloor 2m/n \right \rfloor$

引理：设 $G$$G$ 是 $n$$n$ 阶简单图，若 $\delta (G)\ge \lfloor n/2\rfloor$$\delta(G) \ge \left\lfloor n/2 \right\rfloor$，则 $G$$G$ 必连通

定理 37：设 $G$$G$ 是 $n$$n$ 阶简单图，若 $\delta (G)\ge \lfloor n/2\rfloor$$\delta(G) \ge \left\lfloor n/2 \right\rfloor$，则 $\lambda (G)=\delta (G)$$\lambda(G)=\delta(G)$

图 $G$$G$ 的顶点数为 $n$$n$ 且 $7$$7$ 连通，则其边数至少为 $\lceil \frac{7n}{2}\rceil$$\left \lceil \frac{7n}{2} \right \rceil$

提到割边一定要想到「K2」；提到割点一定要想到「自环」「八字形的图」「K2」；提到块一定要想到「阶数至少为 3」

点连通不能推出点割「完全图不存在点割」，但边连通可以推出边割

点连通可以推出边连通，但反过来就不行

阶数为 $1$$1$ 的块，要么是孤立点，要么是自环

只有一条边的块，要么是自环，要么是 $K_2$$K_2$

至少有三个点的块无环、无割边

定理 32：设图 $G$$G$ 的阶至少为 $3$$3$，则 $G$$G$ 是块当且仅当 $G$$G$ 无环并且任意两点都位于同一个圈上

推论：设 $G$$G$ 的阶至少为 $3$$3$，则 $G$$G$ 是块当且仅当 $G$$G$ 无孤立点且任意两条边都在同一个圈上

E 图 & H 图

欧拉图和哈密尔顿图都有一个大前提：均为连通图

欧拉图一定没有割边，但可能有割点 (八字形的图)

非平凡欧拉图中一定有圈

至少具有 $2$$2$ 个点的无环欧拉图一定是 $2$$2$ 边连通的

完全偶图 $K_{m,n}(m,n\ge 2$$K_{m,n} (m,n\ge 2$ 且均为偶数 $)$$)$，则在其最优欧拉环游中共含 $mn$$mn$ 条边

存在自环的哈密尔顿图有割点；哈密尔顿简单图中一定不存在割点

满足 Dirac 定理、Ore 定理、度序列判定定理的图的闭包一定是完全图

哈密尔顿图：一必要 $(\omega (G-S)\le |S|)$$(\omega(G-S)\le|S|)$，三充分 $(\delta (G)\ge \frac{n}{2}，d(u)+d(v)\ge n，\text{闭}\text{包}\text{是}\text{完}\text{全}\text{图})$$(\delta(G)\ge \frac{n}{2}，d(u) + d(v) \ge n，闭包是完全图)$，一充要 (闭包是 $H$$H$ 图)

若图 $G$$G$ 的闭包是哈密尔顿图，则其闭包不一定是完全图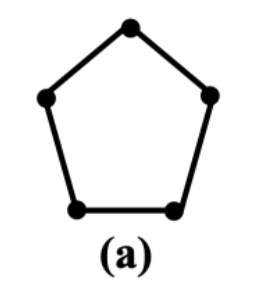

具有 $5$$5$ 个点的度极大非哈密尔顿图族为 $C_{1,5}$$C_{1,5}$ 和 $C_{2,5}$$C_{2,5}$

定理 51 (Chvátal 1972)：若 $G$$G$ 是 $n\ge 3$$n\ge 3$ 的非 $H$$H$ 简单图，则 $G$$G$ 度弱于某个 $C_{m,n}$$C_{m,n}$ 图

$n$$n$ 阶完全图中 $H$$H$ 圈的个数为 $(n-1)!$$(n − 1)!$

匹配与因子分解

超方体 $Q_n$$Q_n$ 的最小覆盖包含的点数为 $2^{n-1}$$2^{n-1}$

图 $K_{m,n}(m\le n)$$K_{m,n}\ (m \le n)$ 的最小覆盖包含的点数为 $m$$m$

因子分解总结为 $3$$3$ 个方面「有没有」「能不能」「数一数」

小 Tips

老师的原话！！还没来得及整理，较为粗糙，凑合看吧！！有时间再整理！！！

题型：

• 5 填空题 （3 分/每个）
• 5 选择题（3 分/每个）
• 7 个解答题（10 分/每题）

极图（非常重要）

最短路算法

最小生成树

虽然学过的概念非常多，但是考试中的概念是重点中的重点，所以很多知识点考察不到

有些知识点只知道概念即可 (掌握概念)，有些知识点了解即可 (可以不管)

第一章 邻接谱 只需要掌握 $K_n$$K_n$ 的邻接谱即可

第二章 树的中心 & 形心 概念掌握即可

第三章 宽距离 & 宽直径 概念掌握即可

第四章 线图 & 超哈密尔顿图 概念掌握即可

第七章重点

特殊图的点色数，边色数（填空题）

以点着色和边着色为模型的应用题

求一个具体图的色多项式，并且还要求出该图的点色数（基本都会考，只有一年没考）

• 根据「理想子图」求色多项式，注意是补图
• 根据色多项式求原图的点色数，见作业 4 最后一道应用题

第八章 Ramsey 数 只需知道 $R(3,3)=6;R(4,4)=18$$R(3,3) = 6; \ R(4,4) = 18$；点临界图 & 边临界图 不考

超哈密尔顿图：本身不是哈密尔顿图，任意删去一个点，变成哈密尔顿图，例如：彼得森图

总结 $k$$k$ 正则二部图

考察基本概念的正确理解，主要结论的灵活应用，不会考某一个定理的证明，结论的证明一般都不会考，除了一些高频考题外

着重注意曾经考过的题目

证明是哈密尔顿图

找出哈密尔顿圈就行了