Kruskal 最小生成树算法

1584. 连接所有点的最小费用

首先弄清楚最小生成树概念之前，请先弄清楚 「生成子图」「树」「生成树」概念

• 生成子图：一个图的生成子图指顶点集相同，边集可不同的子图 -> 详情见 图论--定义 10
• 树：不含圈的连通图称为树 -> 详情见 图论--定义 35
• 生成树：若图 $G$$G$ 的生成子图 $T$$T$ 是树，则称 $T$$T$ 为 $G$$G$ 的生成树 -> 详情见 图论--定义 40
• 最小生成子树：在连通赋权图 $G$$G$ 中，边权之和最小的生成树称为 $G$$G$ 的最小生成树 -> 详情见 图论--定义 43

可利用图的连通性来解决最小生成树的问题，很容易想到可以运用「并查集」算法来辅助生成最小生成树

关于并查集算法的详细总结可点击该处 -> 并查集

针对上述四个概念，我们一一来分析并提出解决方案

• 问题一：如何判断一个图是否为原图的生成子图
• 问题二：如何判断生成子图是一棵树
• 问题三：如何获得最小生成树

问题一：利用并查集的连通分支的数量来判断

设顶点集的数量为 n，并查集中的节点数同为 n，一一对应

若最终并查集的连通分支数量为 1，则表明所有节点都在同一连通分支中，即子图为生成子图；反之则在多个分支中

总结就是，对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环

问题二：利用并查集的连通性来判断

显而易见，如果在一个连通分支中，新增一条边，则会出现环/圈

故每次进行union(u,v)操作时前进行判断，如果connected(u,v)==true，则跳过。这样就可以保证生成子图是一棵树

问题三：对边进行非递减排序，从权值小的开始得到生成子树

对于算法的形象化模拟可以看下面动图

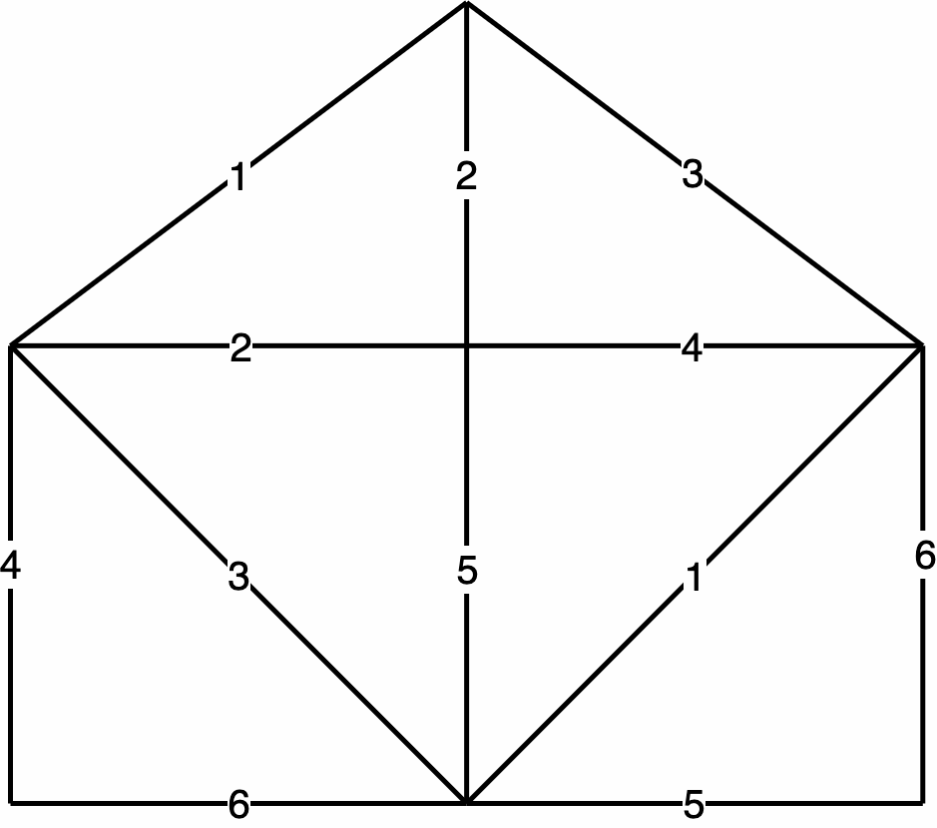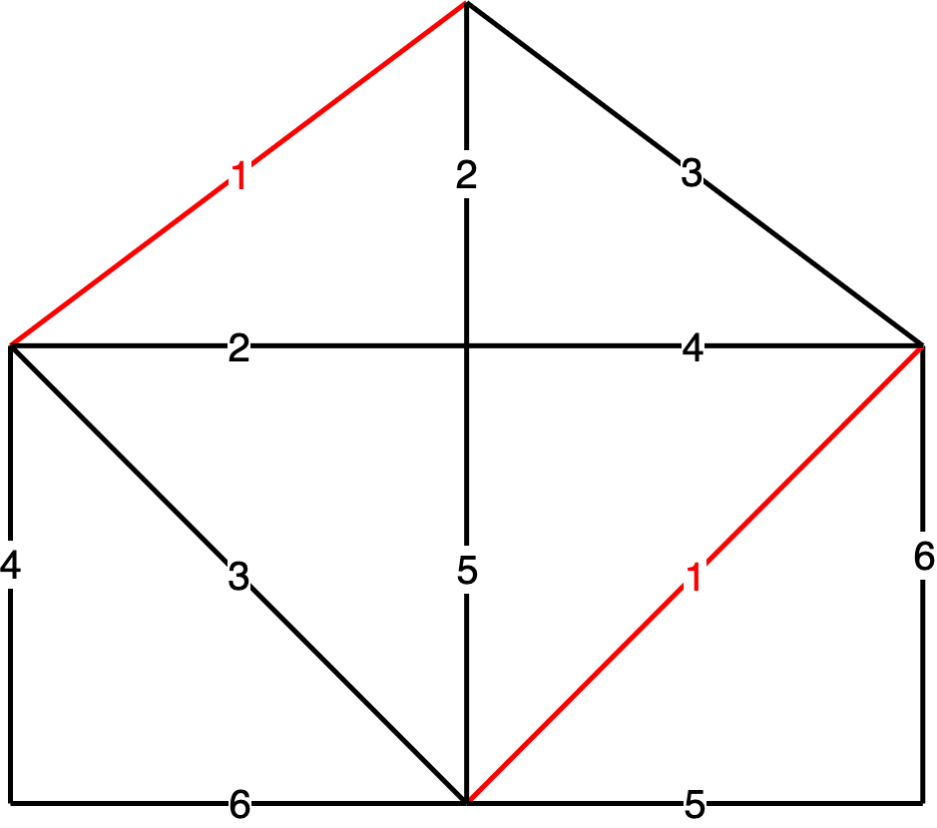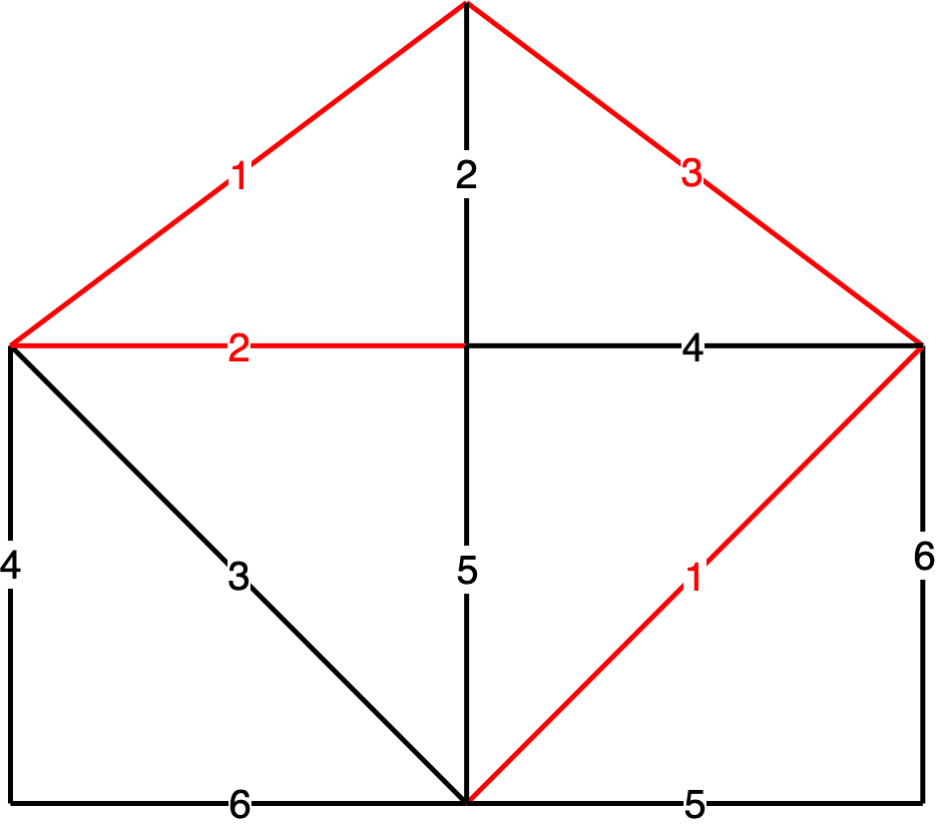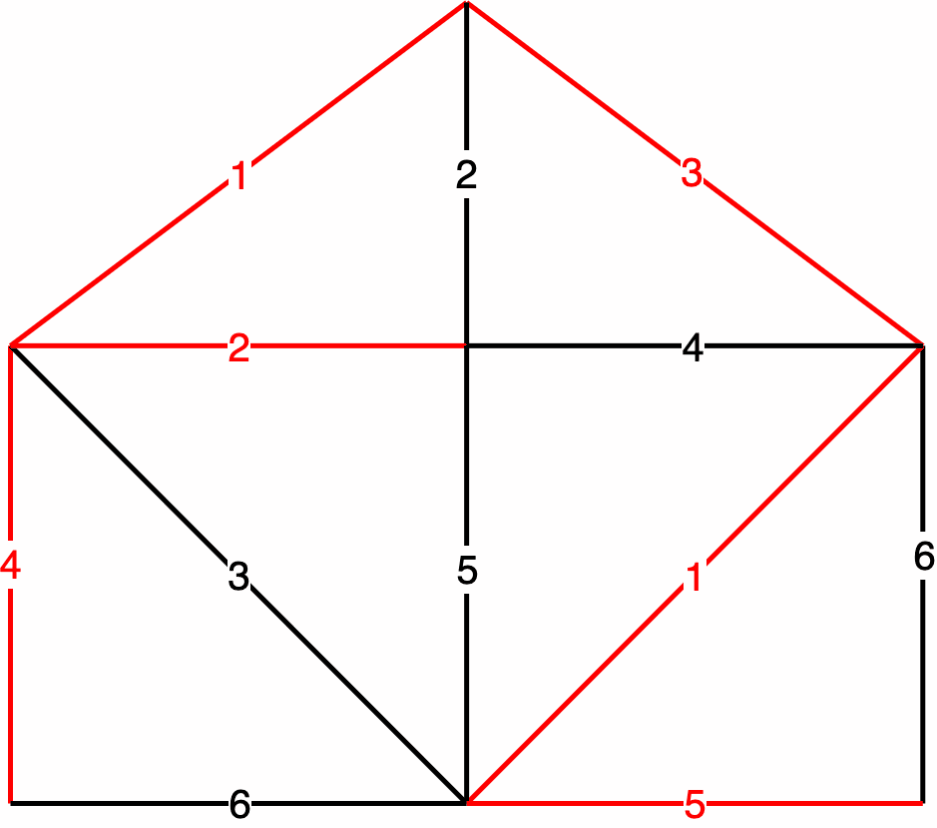
关于 Kruskal 算法的核心思想 可见 图论 -- Kruskal 算法部分

算法模版

​x
int minimumCost(int n, int[][] edges) {
    // 编号为 0...n
    UF uf = new UF(n + 1);
    // 对所有边按照权重从小到大排序
    Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
    // 记录最小生成树的权重之和
    int mst = 0;
    for (int[] edge : edges) {
        int u = edge[0];
        int v = edge[1];
        int weight = edge[2];
        // 若这条边会产生环，则不能加入 mst
        if (uf.connected(u, v)) {
            continue;
        }
        // 若这条边不会产生环，则属于最小生成树
        mst += weight;
        uf.union(u, v);
    }
    // 保证所有节点都被连通
    // uf.count() == 1 说明所有节点被连通
    return uf.count() == 1 ? mst : -1;
}

class UF {
    // 见 并查集总结 的实现
}