Prim 最小生成树算法

关于 Prim 算法的核心思想 可见 图论 -- Prim 算法部分

对于算法的形象化模拟可以看下面动图

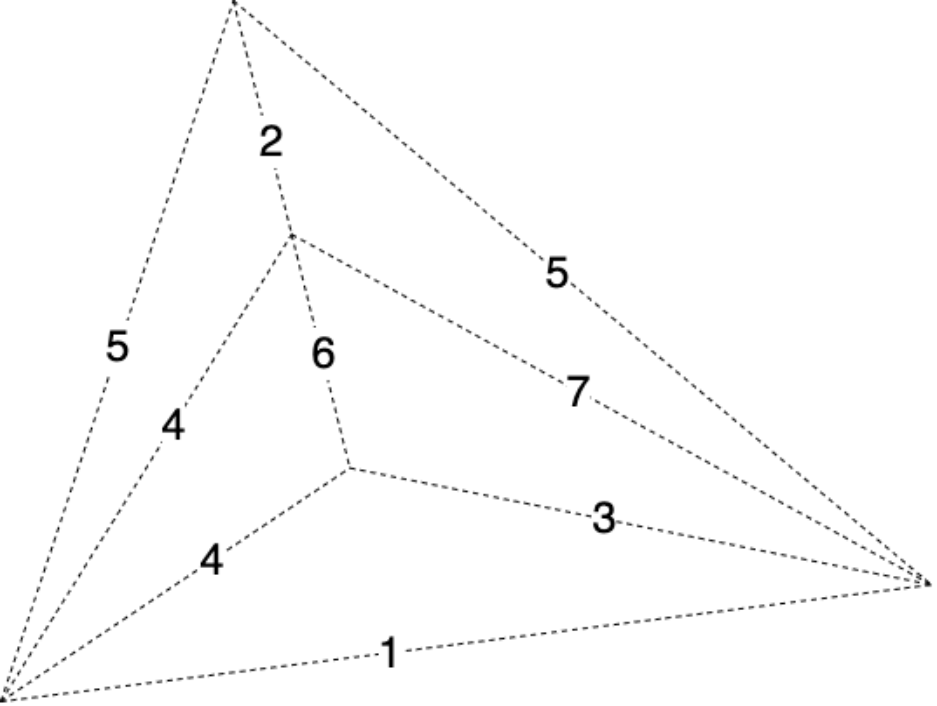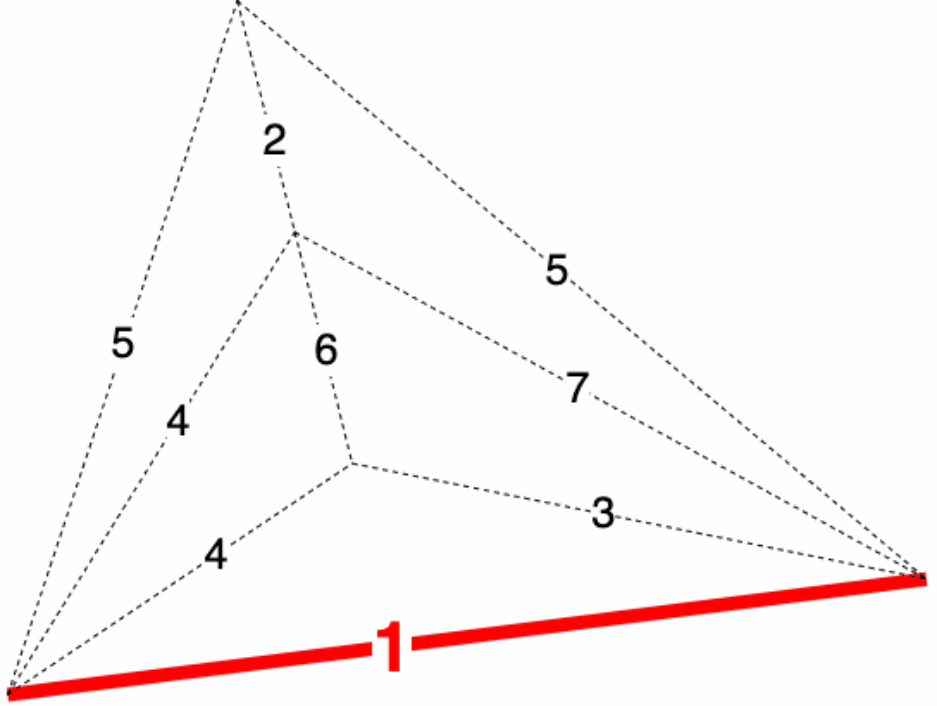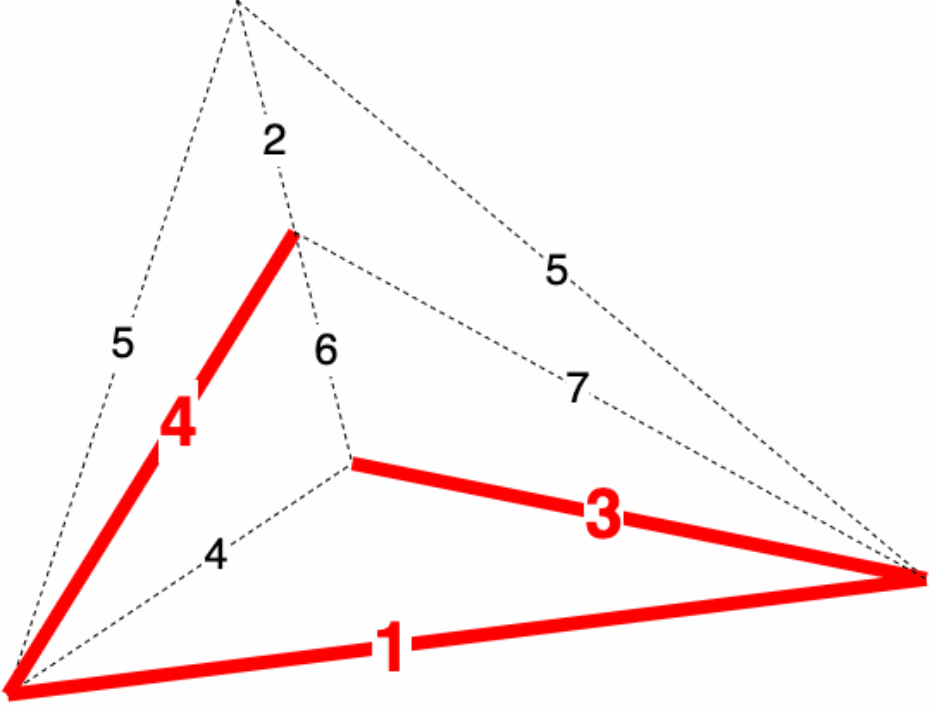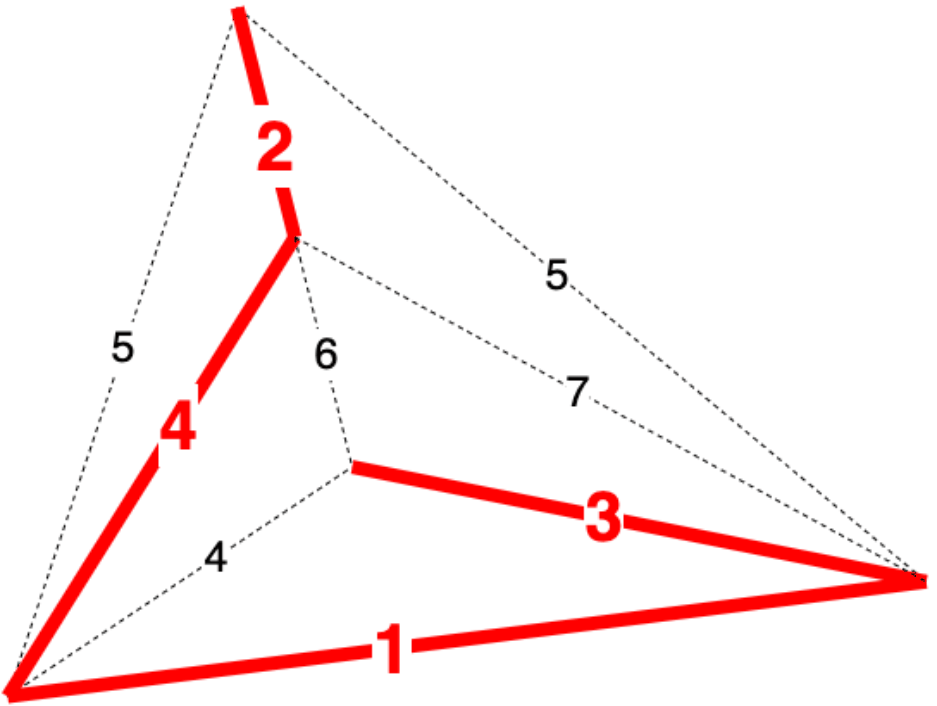
下面和 Kruskal 算法一样，解释以下三个问题，可与 Kruskal 算法对比观看

• 问题一：如何判断一个图是否为原图的生成子图
• 问题二：如何判断生成子图是一棵树
• 问题三：如何获得最小生成树

问题一：利用inMST[]数组来判断所有节点是否已在生成树中，详细实现可见allConnected()方法

问题二：利用inMST[]数组来记录已加入生成树中的节点，以保证无环

问题三：利用优先队列按照边的权重从小到大排序，可保证最终的生成子树为最小生成子树

算法模版

​x
public class Prim {
    // 存在横切边的数据结构
    private final Queue<int[]> pq;
    // 记录已经成为最小生成树的节点
    private boolean[] inMST;
    // 记录最小生成树的权重和
    private Integer weightSum = 0;
    // graph 是用邻接表表示的一幅图
    // graph[s] 记录节点 s 所有相邻的边
    // 三元组 int[]{from, to, weight} 表示一条边
    private final List<int[]>[] graph;

    public Prim(List<int[]>[] graph) {
        this.graph = graph;
        // 按照边的权重从小到大排序
        this.pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[2]));
        // 图中有 n 个节点
        int n = graph.length;
        this.inMST = new boolean[n];
        // 随便从一个点开始切分都可以，我们不妨从节点 0 开始
        inMST[0] = true;
        cut(0);
        // 不断进行切分，向最小生成树中添加边
        while (!pq.isEmpty()) {
            int[] edge = pq.poll();
            int to = edge[1];
            int weight = edge[2];
            if (inMST[to]) {
                // 节点 to 已经在最小生成树中，跳过
                // 否则这条边会产生环
                continue;
            }
            // 将边 edge 加入最小生成树
            weightSum += weight;
            inMST[to] = true;
            // 节点 to 加入后，进行新一轮切分，会产生更多横切边
            cut(to);
        }
    }
    // 将 s 的横切边加入优先队列
    private void cut(int x) {
        // 遍历 s 的邻边
        for (int[] edge : graph[x]) {
            int to = edge[1];
            if (inMST[to]) {
                // 相邻接点 to 已经在最小生成树中，跳过
                // 否则这条边会产生环
                continue;
            }
            // 加入横切边队列
            pq.offer(edge);
        }
    }
    // 最小生成树的权重和
    public int weightSum() {
        return this.weightSum;
    }
    // 判断最小生成树是否包含图中的所有节点
    public boolean allConnected() {
        for (int i = 0; i < graph.length; i++) {
            if (!inMST[i]) {
                return false;
            }
        }
        return true;
    }
}